
Введение
В последние годы повсеместные нейронные сети находят все больше применений в различных областях знаний, вытесняя классические алгоритмы, использовавшиеся многие годы.Область компьютерного зрения не является исключением, где год за годом все больше задач решаются с помощью современных нейронных сетей.
Пришло время написать об еще одном павшем бойце в войне традиционного видения против глубокого обучения.
Многие годы в задаче поиска локальных особенностей изображений (так называемых ключевых точек) доминировал алгоритм SIFT (Scale-invariant Feature Transform), предложенный еще в 1999 году.
Многие погибли в попытках его превзойти, но только глубокое обучение удалось.
Итак, встречайте новый алгоритм поиска локальных признаков — LIFT (Learned Invariant Feature Transform).
Потребность в данных

Чтобы глубокое обучение работало, вам нужно много данных, иначе волшебства не произойдет. И нам нужны не просто данные, а данные, которые будут репрезентативным представлением проблемы, которую мы хотим решить.
Итак, давайте посмотрим, на что способны искусственные детекторы/дескрипторы характерных точек:
- Инвариантность к местоположению на картинке.
- Инвариантность к углу поворота.
- Масштабная инвариантность.
Вы, конечно, можете взять произвольные изображения, вырезать из них точки, а затем применить синтетически сгенерированные аффинные преобразования, чтобы получить набор данных любого размера.
Но синтетика плоха, потому что всегда есть какие-то ограничения на точность моделирования.
реальные случаи.
Реальные наборы данных, соответствующие нашим требованиям, возникают при решении некоторых прикладных задач компьютерного зрения.
Например, при 3D-реконструкции сцены, снятой с разных ракурсов, мы делаем что-то вроде этого:
- Для каждого изображения сцены находим специальные точки.
- Находим соответствия между особыми точками на разных изображениях.
- Но на основе этой информации мы рассчитываем пространственное положение каждого кадра (параметризуемое через
те.вращение и перемещение относительно начала координат).
- С помощью процедуры триангуляции находим трехмерные положения всех особых точек.
- Использование обширной оптимизации, т.е.
Регулировка комплекта (чаще всего алгоритм, полученный на основе метода Левенберга-Марквардта), мы получаем более точную информацию о расположении точек в пространстве.
- Все виды постобработки.
Например, вы можете растянуть полигональную модель на облако точек, чтобы получить гладкие поверхности.
Это облако — именно тот набор данных, который нам нужен.
Особо не заморачиваясь тонкостями Structure From Motion, авторы работы взяли пару общедоступных наборов данных для 3D-реконструкции, прогнали их через общедоступный инструмент для построения облака точек (VisualSFM), а затем использовали полученный набор данных.
в своих экспериментах.
Утверждается, что сетка, обученная на таком наборе, также распространяется на другие типы сцен.
Сетки, сетки, сетки

С датасетом мы разобрались, поэтому пора переходить к самому интересному, а именно к изучению сеток.
Всю сетку можно разделить на 3 логических блока:
- Детектор – отвечает за поиск особых точек на всем изображении в целом.
- Rotation Estimator — определяет ориентацию точки и вращает патч вокруг нее так, чтобы угол поворота стал нулевым.
- Дескриптор — принимает на вход патч, из которого конструирует уникальный (вот получается) вектор, описывающий этот патч.
Эти векторы уже можно использовать, например, чтобы вычислить евклидово расстояние между парой точек и понять, похожи они или нет.
Вывод

Поиск особых точек и вычисление их дескрипторов происходит в несколько этапов:
- Сначала мы строим пирамиду изображения (т. е.
уменьшаем исходное изображение до нескольких масштабов для получения масштабно-инвариантных признаков) для исходного изображения.
- Мы прогоняем каждый слой пирамиды через сеть детекторов и вычисляем пирамиду карт оценок.
- С помощью процедуры немаксимального подавления находим наиболее сильных кандидатов на специальные баллы.
- Для каждой особой точки мы вырезаем участок, включающий в себя особую точку и часть ее окрестностей.
- Мы выравниваем ориентацию каждого патча с помощью средства оценки ориентации.
- Мы вычисляем дескриптор для каждого выровненного патча.
- Используем полученные дескрипторы для стандартной процедуры сопоставление функций .
Дескриптор
Со времен SIFT-функций известно, что даже если мы не особенно хорошо умеем находить действительно уникальные точки, но можем построить крутой дескриптор для каждой из них, то, скорее всего, нам удастся решить задачу.Поэтому начнем обзор с конца, а именно с построения дескриптора для уже найденной особой точки.
Вообще говоря, любая сверточная сетка, принимая на вход картинку (патч), выдаёт на выходе некое описание этой картинки, которое уже можно использовать в качестве дескриптора.
Но, как показывает практика, не обязательно брать огромную сеть, такую как, например, VGG16, ResNet-152, Inception и т. д., нам достаточно небольшой сети: 2-3 сверточных слоя с активациями в виде гиперболических тангенсов
и другие мелочи типа пакетной нормализации и т.д. Для конкретики обозначим наш сетевой дескриптор
, Где
— дескрипторная сверточная сеть,
- его параметры,
— патч с нулевым углом (полученный из средства оценки вращения).
Для каждой особой точки составим две пары:
-
— пара патчей, соответствующих проекциям одной и той же особой точки. -
- пара патчей, где первый принадлежит особой точке, а второй (отрицательный образец) - нет. В этом случае «негативный» участок выбирается из определенной окрестности, не слишком далекой от положительной.По мере обучения окрестность становится меньше, поэтому отрицательные образцы становятся все труднее.
Те.
По сути, мы хотим, чтобы евклидово расстояние между подобными точками было небольшим, а между разнородными точками — большим.
Оценщик вращения
Поскольку мы можем наблюдать одну и ту же точку не только из разных точек пространства, но и под разными углами наклона, мы должны уметь построить один и тот же дескриптор для одной и той же специальной точки независимо от того, под каким углом мы ее наблюдаем.Но вместо того, чтобы учить Дескриптор запоминать все возможные углы наклона одной и той же точки, предлагается использовать промежуточный вычислительный блок, который будет определять ориентацию заплатки в пространстве (Rotation Estimator) и «поворачивать» заплатку на какую-то из своих точек.
состояние, инвариантное к вращению (пространственное преобразование).
Конечно, можно было бы использовать блок расчета ориентации патча в пространстве, взятый из алгоритма построения SIFT-признаков, но сейчас 21 век и сейчас каждую задачу компьютерного зрения принято сводить к машинному обучению.
.
Поэтому для решения этой проблемы мы воспользуемся другой сверточной нейронной сетью.
Итак, обозначим нашу нейронную сеть как:
, Где
- параметры сети и
- оригинальный патч.
Возьмем пары патчей в качестве обучающей выборки
,
, принадлежащие одной особой точке, но имеющие разные углы наклона, а также их пространственные координаты
,
.
В процессе обучения мы будем минимизировать следующую функцию потерь:
Где
— заплатка, полученная после процедуры исправления ее ориентации,
.
Те.
При обучении сети мы вращаем патчи с разными углами наклона так, чтобы евклидово расстояние между их дескрипторами стало минимальным.
Детектор
Осталось рассмотреть последний шаг, а именно непосредственное обнаружение особых точек на исходном изображении.Суть этой сети заключается в том, что через нее проходит все изображение, а на выходе ожидается карта объектов, для которой сильные отклики соответствуют особым точкам исходного изображения.
Несмотря на то, что при выводе модели детектор запускается сразу на всем изображении, в процессе обучения мы будем запускать его только для отдельных патчей.
Расчет детектора состоит из двух шагов: сначала мы должны рассчитать Score Map для патча, который затем будет использоваться для определения положения особой точки:
а затем вычислите положение особой точки:
Где
это функция, которая вычисляет взвешенный центр масс, при этом веса являются результатом расчета.
:
где y — позиция внутри карт очков,
— гиперпараметр, отвечающий за коэффициент «размытия» функции softmax. При обучении детектора мы возьмем четыре патча
, Где
- проекции одной и той же особой точки,
- проекция другой особой точки,
— патч, не принадлежащий особой точке.
Для набора таких патчей минимизируем следующую функцию потерь:
Где
— параметр балансировки двух членов функции потерь.
Участник потерь, ответственный за правильную классификацию на положительные и отрицательные:
Член потерь, отвечающий за точную локализацию особых точек:
Обучение
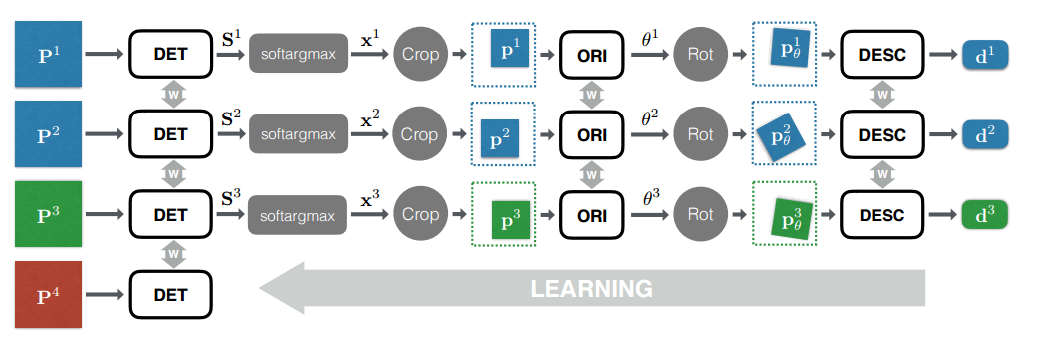
Вся сеть обучается модным сейчас способом End-To-End, т.е.
все части сети сразу обучаются параллельно, как сиамские сети.
В этом случае для каждого из 4 используемых при обучении патчей создается отдельная ветвь сети с общими между ними весами.
Ээксперименты 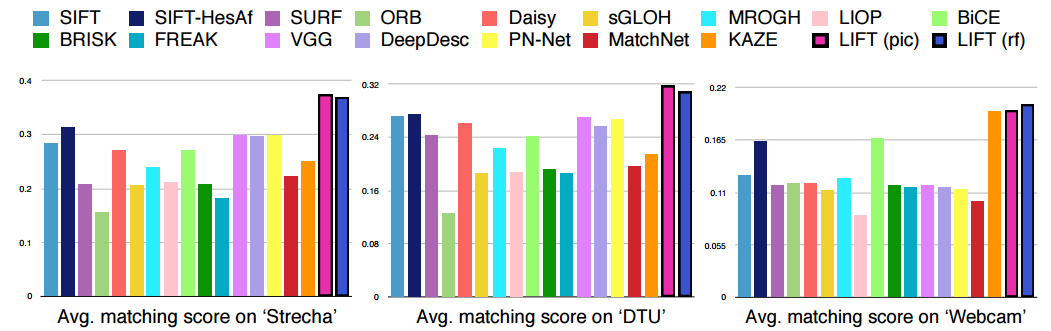
Сравнив с ранее существовавшими методами поиска особых точек, авторы пришли к выводу, что их подход является современным.
А результаты их сети можно увидеть на следующем видео: Заключение Представленная работа является еще одним подтверждением того, что время традиционных методов компьютерного зрения уходит, и на смену ему приходит эра науки о данных.
И снова, придумывая гениальную эвристику, решающую какую-то сложную задачу, стоит задуматься: а можно ли сформулировать задачу так, чтобы компьютер мог самостоятельно перебрать миллионы эвристик и выбрать ту, которая решает задачу? наилучшим образом.
Ссылки
- Оригинал статьи можно найти на arxiv: LIFT: преобразование изученных инвариантных признаков
- В Theano на github есть вполне дружественный код: https://github.com/cvlab-epfl/LIFT
- Вы можете прочитать об обучении сиамских сетей и аналогичном конвейере для вычисления дескрипторов особых точек, но применительно к проблеме стереосопоставления, от нашего отца Янна ЛеКуна здесь: Стереосопоставление путем обучения сверточной нейронной сети для сравнения фрагментов изображений
P.S. Этот пост является результатом обсуждения кружки , а потому стиль автора может быть недостаточно литературным.
Теги: #машинное обучение #глубокое обучение #компьютерное зрение #Алгоритмы #Обработка изображений #Машинное обучение

-
Как Ремонтируют Атомные Реакторы
19 Oct, 24 -
Cyanogenmod 10.1 - Полный Обзор
19 Oct, 24


