Начнем с объяснения того, что такое четырехмерное пространство.
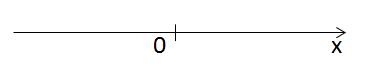
Это одномерное пространство, то есть как раз ось ОХ.
Любая точка на нем характеризуется одной координатой.
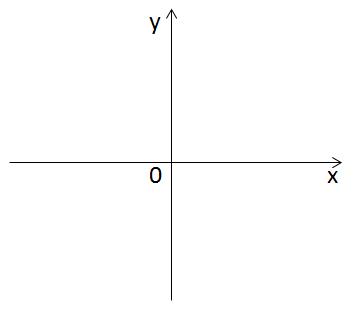
Теперь нарисуем ось OY перпендикулярно оси OX. Итак, мы получаем двумерное пространство, то есть плоскость XOY. Любая точка на нем характеризуется двумя координатами – абсциссой и ординатой.
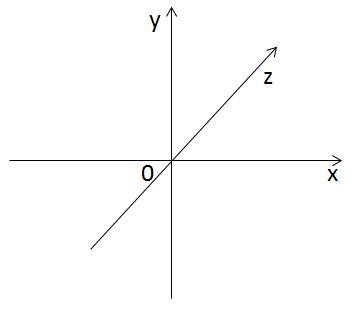
Проведем ось OZ перпендикулярно осям OX и OY. В результате получается трехмерное пространство, в котором любая точка имеет абсциссу, ординату и аппликату.
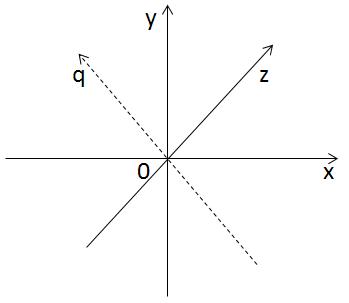
Логично, что четвертая ось OQ должна быть перпендикулярна осям OX, OY и OZ одновременно.
Но мы не можем точно построить такую ось, а потому можем лишь попытаться ее представить.
Каждая точка в четырехмерном пространстве имеет четыре координаты: x, y, z и q. Теперь посмотрим, как появился четырехмерный куб.
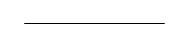
На картинке изображена фигура в одномерном пространстве – линия.
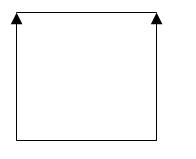
Если сделать параллельный перенос этой линии по оси OY, а затем соединить соответствующие концы двух получившихся линий, то получится квадрат. 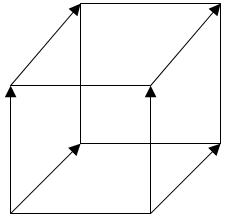
Аналогично, если сделать параллельный перенос квадрата по оси OZ и соединить соответствующие вершины, то получится куб.
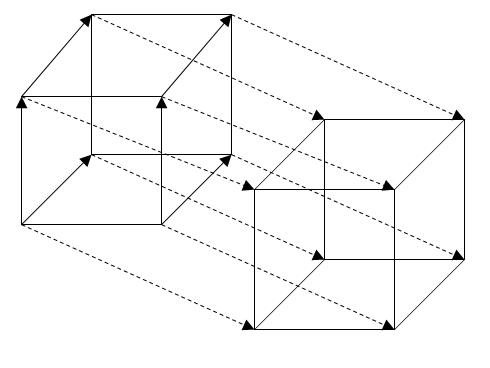
А если сделать параллельный перенос куба по оси OQ и соединить вершины этих двух кубов, то получится четырехмерный куб.
Кстати, это называется тессеракт .
Чтобы нарисовать куб на плоскости, вам понадобится проект .
Визуально это выглядит так: 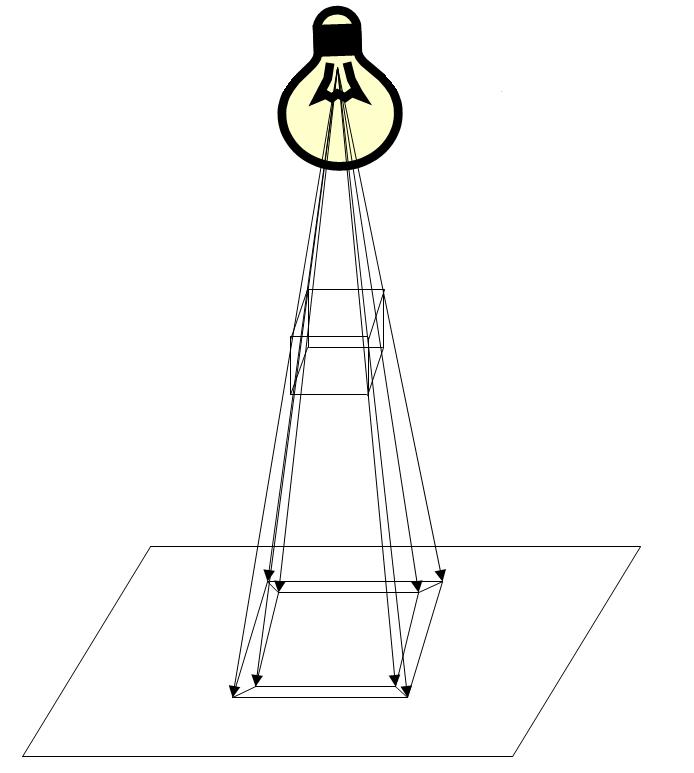
Представим, что он висит в воздухе над поверхностью.
каркасная модель куб, то есть как бы «сделанный из проволоки», а над ним лампочка.
Если включить лампочку, обвести карандашом тень куба, а затем выключить лампочку, то на поверхности будет изображена проекция куба.
Давайте перейдем к чему-то немного более сложному.
Посмотрите еще раз на рисунок с лампочкой: как видите, все лучи сходятся в одной точке.
Это называется крайний предел; точка схода и используется для создания перспективная проекция (а может быть и параллельным, когда все лучи параллельны друг другу.
В результате ощущение объёма не создаётся, но становится светлее, и причём, если точка схода находится достаточно далеко от проецируемого объекта , то разница между этими двумя проекциями мало заметна).
Чтобы спроецировать данную точку на заданную плоскость с помощью точки схода, нужно провести прямую через точку схода и данную точку, а затем найти точку пересечения полученной прямой и плоскости.
А чтобы спроецировать более сложную фигуру, скажем, куб, нужно спроецировать каждую его вершину, а затем соединить соответствующие точки.
Необходимо отметить, что алгоритм проецирования пространства на подпространство можно обобщить на случай 4D-> 3D, а не только 3D-> 2D. Как я уже сказал, мы не можем точно представить, как выглядит ось OQ, как и тессеракт. Но мы можем получить о нем ограниченное представление, если спроецируем его на объем, а затем нарисуем на экране компьютера! Теперь поговорим о проекции тессеракта.
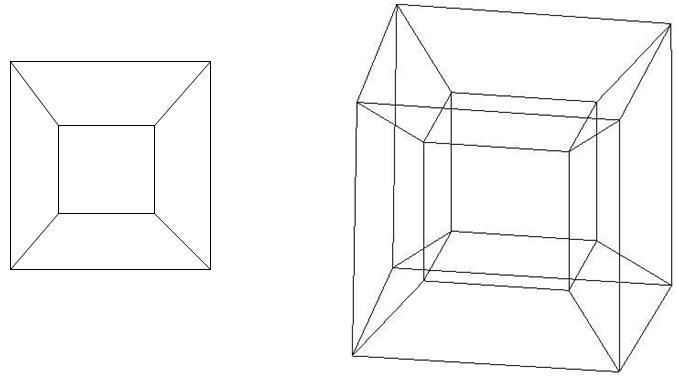
Слева — проекция куба на плоскость, а справа — тессеракт на объем.
Они очень похожи: проекция куба выглядит как два квадрата, маленький и большой, находящиеся один внутри другого, соответствующие вершины которых соединены линиями.
А проекция тессеракта выглядит как два куба, маленький и большой, находящиеся один внутри другого, и соответствующие вершины которых соединены.
Но куб мы все видели, и можем с уверенностью сказать, что и малый квадрат, и большой, и четыре трапеции вверху, внизу, справа и слева от маленького квадрата на самом деле являются квадратами, и они равны.
.
И в тессеракте то же самое.
И большой куб, и маленький куб, и шесть усеченных пирамид на гранях маленького куба — это все кубы, и они равны.
Моя программа умеет не только рисовать проекцию тессеракта на объём, но и вращать его.
Давайте посмотрим, как это делается.
Сначала я расскажу вам, что это такое вращение параллельно плоскости .
Представьте, что куб вращается вокруг оси OZ. Тогда каждая его вершина описывает окружность вокруг оси OZ. 
Круг – плоская фигура.
И плоскости каждой из этих окружностей параллельны друг другу и в данном случае параллельно плоскости XOY. То есть речь может идти не только о вращении вокруг оси OZ, но и о вращении параллельно плоскости XOY. Как мы видим, для точек, которые вращаются параллельно оси XOY, меняются только абсцисса и ордината, а аппликат остается неизменным.
И, по сути, о вращении вокруг прямой мы можем говорить только тогда, когда имеем дело с трёхмерным пространством.
В двухмерном пространстве все вращается вокруг точки, в четырехмерном все вращается вокруг плоскости, в пятимерном пространстве мы говорим о вращении вокруг объема.
И если мы можем представить себе вращение вокруг точки, то вращение вокруг плоскости и объема – это нечто немыслимое.
А если говорить о вращении параллельно плоскости, то в любом n-мерном пространстве точка может вращаться параллельно плоскости.
Многие из вас наверняка слышали о матрице вращения.
Умножив на нее точку, получим точку, повернутую параллельно плоскости на угол фи.
Для двумерного пространства это выглядит так: 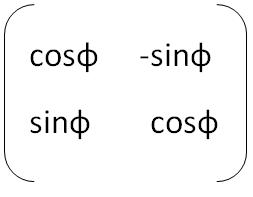
Как умножать: x точки, повернутой на угол phi = косинус угла phi*ix исходной точки минус синус угла phi*ig исходной точки;
ig точки, повернутой на угол phi = синус угла phi * ix исходной точки плюс косинус угла phi * ig исходной точки.
Xa`=cosф*Xa – грех*Ya Ya`=sinф*Xa + cosф*Ya , где Xa и Ya — абсцисса и ордината поворачиваемой точки, Xa` и Ya` — абсцисса и ордината уже повернутой точки.
Для трехмерного пространства эта матрица обобщается следующим образом: 
Вращение параллельно плоскости XOY. Как видите, координата Z не меняется, а меняются только X и Y.
Ха`=cosф*Ха – грех*Я + За*0
Ya`=sinф*Xa +cosф*Ya + Za*0
Za`=Xa*0 + Ya*0 + Za*1 (по сути, Za`=Za) 
Вращение параллельно плоскости XOZ. Ничего нового,
Xa`=cosф*Ха + Ya*0 – sinф*Za
Ya`=Xa*0 + Ya*1 + Za*0 (по сути Ya`=Ya)
Za`=sinф*Xa + Ya*0 + cosф*Za 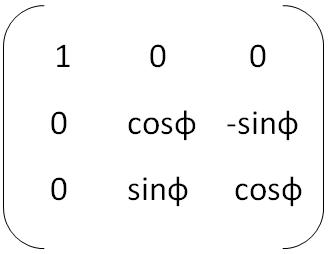
И третья матрица.
Xa`=Xa*1 + Ya*0 + Za*0 (по сути, Xa`=Xa)
Ya`=Xa*0 + cosф*Ya – sinф*Za
Za`=Xa*0 + sinф*Ya + cosф*Za
А для четвертого измерения они выглядят так: 
Думаю, вы уже поняли, на что умножать, поэтому не буду еще раз вдаваться в подробности.
Но замечу, что он делает то же самое, что и матрица для вращения параллельно плоскости в трёхмерном пространстве! Обе они меняют только ординату и аппликату, а остальные координаты не затрагивают, поэтому ее можно использовать в трехмерном случае, просто не обращая внимания на четвертую координату.
А вот с формулой проекции не все так просто.
Сколько бы форумов я ни читал, ни один из методов проекции мне не помог.
Параллельный мне не подошел, так как проекция не выглядела бы трехмерной.
В некоторых формулах проекции, чтобы найти точку, нужно решить систему уравнений (а я не знаю, как научить компьютер их решать), других я просто не понял.
В общем, решил придумать свой путь.
Для этого рассмотрим проекцию 2D-> 1D. 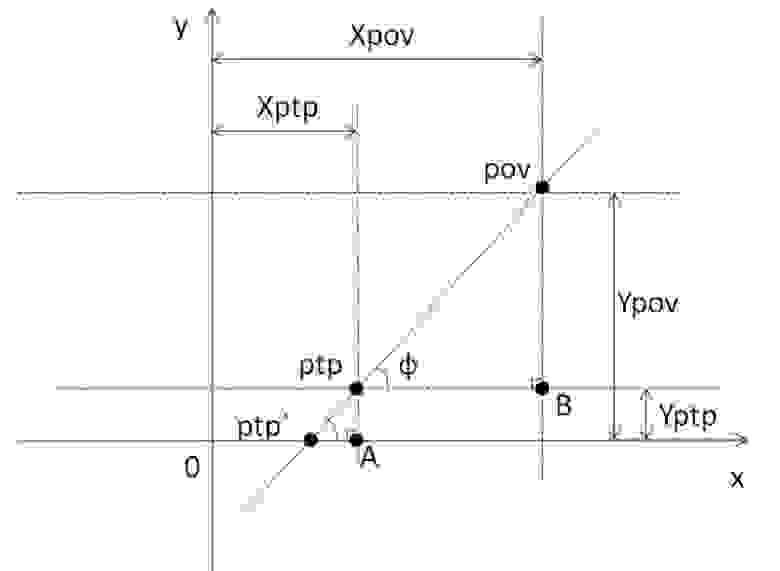
pov означает «Точка зрения», ptp означает «Точка проецирования» (точка проецирования), а ptp` — желаемая точка на оси OX.
Углы povptpB и ptpptp`A равны соответственно (пунктир параллелен оси OX, прямая povptp — секущая).
x точки ptp` равен x точки ptp минус длина отрезка ptp`A. Этот отрезок можно найти из треугольника ptpptp`A: ptp`A = ptpA/тангенс угла ptpptp`A. Эту касательную можно найти из треугольника povptpB: тангенс ptpptp`A = (Ypov-Yptp)(Xpov-Xptp).
Ответ: Xptp`=Xptp-Yptp/тангенс угла ptpptp`A. Я не стал здесь подробно описывать этот алгоритм, так как есть много частных случаев, когда формула несколько меняется.
Если кому интересно, посмотрите исходники программы, там в комментариях все описано.
Чтобы спроецировать точку трехмерного пространства на плоскость, мы просто рассмотрим две плоскости — XOZ и YOZ, и решим эту задачу для каждой из них.
В случае четырехмерного пространства необходимо рассматривать три плоскости: XOQ, YOQ и ZOQ. И наконец, о программе.
Работает это так: инициализировать шестнадцать вершин тессеракта -> в зависимости от введенных пользователем команд, повернуть его -> проецировать на объем -> в зависимости от введенных пользователем команд, повернуть его проекцию -> спроецировать на объем.
самолет -> рисовать.
Проекции и вращения я написал сам.
Они работают по формулам, которые я только что описал.
Библиотека OpenGL рисует линии, а также обрабатывает смешивание цветов.
А координаты вершин тессеракта вычисляются таким образом: Координаты вершин линии с центром в начале координат и длиной 2: (1) и (-1); - " - " - квадрат - " - " - и длина ребра 2: (1; 1), (-1; 1), (1; -1) и (-1; -1); - " - " - куб - " - " -: ( 1; 1; 1 ), ( -1; 1; 1), (1; -1; 1), (-1; -1; 1), ( 1; 1; -1 ), ( -1; 1; -1), (1; -1; -1), (-1; -1; -1); Как видите, квадрат находится на одну линию выше оси OY и на одну линию ниже оси OY; куб — это один квадрат перед плоскостью XOY и один за ней; Тессеракт — это один куб на другой стороне объема XOYZ и один на этой стороне.
Но гораздо легче воспринять это чередование единиц и минусов, если они написаны в столбик 1; 1; 1 -1; 1; 1 1; -1; 1 -1; -1; 1 1; 1; -1 -1; 1; -1 1; -1; -1 -1; -1; -1 В первом столбце чередуются единица и минус одна.
Во втором столбце сначала два плюса, затем два минуса.
В третьем – четыре плюса, а потом четыре минуса.
Это были вершины куба.
В тессеракте их в два раза больше, а потому пришлось писать цикл для их объявления, иначе очень легко запутаться.
Моя программа также умеет рисовать анаглиф.
Счастливые обладатели 3D-очков могут наблюдать стереоскопическое изображение.
В рисовании картинки нет ничего сложного; вы просто рисуете на плоскость две проекции для правого и левого глаза.
Но программа становится гораздо нагляднее и интереснее, а главное, дает лучшее представление о четырехмерном мире.
К менее значимым функциям можно отнести подсветку одной из кромок красным цветом, чтобы повороты было лучше видно, а также мелкие удобства вроде настройки координат точек «глаза», увеличения и уменьшения скорости поворота.
Архив с программой, исходным кодом и инструкцией по использованию: www.dropbox.com/s/xilxouqmgnsf6zs/%D0%A2%D0%B5%D1%81%D1%81%D0%B5%D1%80%D0%B0%D0%BA%D1%82.rar (необходимо скачать и установить программу Dropbox: www.dropbox.com ) Источник: docs.google.com/document/d/1sGjBTb-od84Qp_la0LS9tWFZL4aYk-1exUs0Za5_Uq0/edit Теги: #математика #геометрия #четырехмерное пространство #анаглиф #математика
-
Как У Вас Организован Процесс Тестирования?
19 Oct, 24 -
Посвящение Константину Калинову
19 Oct, 24 -
Выпуск Firefox 24 И Firefox 24 Esr
19 Oct, 24


