Прежде всего хотелось бы сказать, что математика помогает привести мысли в порядок и эффективно развивает логическое мышление, а это одни из самых необходимых качеств для участников разработки программного обеспечения.
Говоря о тестировании, речь в основном идет о поведении системы, которое ортогонально структурному представлению, обычному для разработчиков программного обеспечения.
Разница между структурным и поведенческим взглядами заключается в том, что структурный взгляд фокусируется на том, что представляет собой программное обеспечение, а поведенческий взгляд учитывает, что делает программное обеспечение.
Одна из трудностей для тестировщиков заключается в том, что базовая техническая документация или руководство по разработке программного обеспечения обычно пишутся разработчиками и для них, и упор делается в первую очередь на структурную, а не поведенческую информацию.
Конечно, для тестирования очень важны как структурная, так и поведенческая части, поскольку в каждой из этих частей можно найти ошибки программирования.
Именно поэтому мы будем говорить о дискретных математических методах, позволяющих показать связь между структурой программы и ее поведением.
В своей повседневной работе инженеры по обеспечению качества программного обеспечения (QA) работают с формулами, поведением функций и структурами данных.
Они всегда отслеживают и проверяют постоянно меняющееся состояние систем, поэтому им необходимо обладать алгоритмическим и математическим мышлением, чтобы понимать логику программного обеспечения.
Если разработчик использует в своей работе математический подход, в результате все логические операции будут связаны друг с другом, действия будут следовать логической цепочке, а каждая функция будет рассмотрена структурно.
Дискретная математика помогает нам найти оптимальное решение в различных ситуациях.
Например, вы можете найти наиболее подходящий набор тест-кейсов, не охватывая все возможные варианты.
Более того, дискретная математика помогает нам визуализировать именно ту часть программного обеспечения, которая была реализована и охвачена тестами.
К сожалению, мы живем не в идеальном мире, и фактические результаты, ожидаемые от использования программного обеспечения, и фактические результаты могут отличаться.
Итак, основная цель отдела обеспечения качества (QA) — максимально эффективно охватить как можно больше тестовых случаев.
Чтобы показать вам эту концепцию более подробно, мы создали следующую диаграмму Венна на примере, который мы обрисовали ранее: 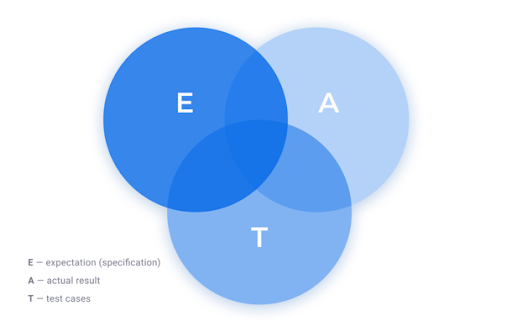
Приведенная выше диаграмма Венна описывает множество ситуаций, тем самым помогая проиллюстрировать и определить наборы ситуаций.
Например, это может помочь нам увидеть различия между наборами объектов.
Дискретная математика помогает анализировать и оптимизировать наборы действий, которые могут повлиять на разрабатываемое программное обеспечение.
Теория множеств
Используя принципы базовой теории множеств, мы можем создать псевдокод, чтобы проиллюстрировать все возможные случаи для приложения Next Day (программы, которая вычисляет следующий день по введенной дате):Этот псевдокод уже подготовлен для разработки и тестирования приложения, поэтому тестировщики также могут применять все возможные тестовые сценарии на основе этих данных.M1={month:month has 30 days} M2={month:month has 31 days except December} M3={month:month is February} M4={month:month is December} D1={day:1<=day<=28} D2={day:1<=day<=29} D3={day:1<=day<=30} D4={day:1<=day<=31} Y1={year:year is a leap year} Y2={year:year is not a leap year}
Использование данных в этом формате помогает увеличить скорость разработки и снижает вероятность ошибок.
Теория графов
Большая часть дискретной математики — это так называемая «теория графов», которая изучает графы.Графы используются для представления взаимосвязей между некоторыми объектами или данными, и компьютерная сеть является подходящим примером графа.
Графики также имеют основополагающее значение для процесса разработки программного обеспечения.
Например, с помощью графа мы можем разложить сложные функции на несколько более мелких частей, что помогает нам более эффективно понимать бизнес-логику.
Графы могут быть направленными и неориентированными, а это значит, что мы можем перемещаться от узла к узлу в одном или в обоих направлениях (в случае ориентированного графа) или не можем переходить от одного узла к другому (если граф направлен в ровно в одном направлении) Итак, вернемся к тестированию программного обеспечения и представим, что у нас есть поток какого-то процесса (например, перемещения задачи в какой-нибудь системе отслеживания задач); у нас есть условие какой-то задачи, и мы можем перенести ее на другой этап (ориентированный граф), а можем достичь какой-то точки, когда уже ничего не можем сделать с сущностью (неориентированный граф).
При таком подходе к визуализации мы легко можем собрать набор всех возможных действий, доступных для данной сущности: 
Давайте продолжим и посмотрим на матрицу смежности, которую можно построить из неориентированного графа.
В примере ниже элементы матрицы смежности указывают, являются ли пары вершин смежными или нет: 
Теперь представьте, что узлы являются термами некоторых сущностей, и если мы построим матрицу смежности для этого графа (набора сущностей), мы увидим конечный набор действий, которые мы можем предпринять.
Например, изменение статуса узла «0» на узел «1» возможно, поскольку они связаны друг с другом.
Но сущность «0» нельзя изменить на стадию «2» или «3», как мы видим из нашей матрицы — в ячейках записан «ноль».
Используя эту матрицу, мы можем исключить ненужные наборы шагов сущности и сократить набор тестовых случаев.
Другая матрица, которую мы можем использовать для сбора тестовых случаев, — это матрица инцидентности, которая показывает связь между двумя классами объектов.
На следующем рисунке мы видим неориентированный граф и его матрицу инцидентности: «1», «2», «3» и «4» — узлы (сущности), «e1», «e2», «e3», «e4» — это узлы.
ребра графа, а матрица иллюстрирует объекты и действия, которые мы можем с ними выполнять.
С узлом «1» мы можем выполнять действия «е1», «е2» и «е3», но действие «е4» для узла «1» недоступно.
Этот метод очень полезен при создании набора тестовых примеров.
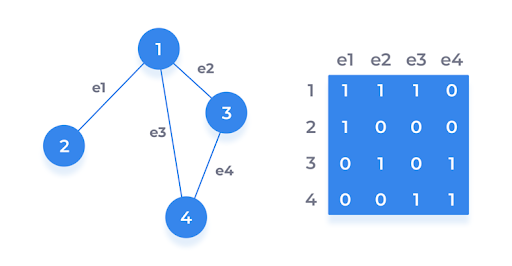
Представим, что тестер получил список сущностей и действий, которые можно выполнить с этими сущностями.
Используя эту матрицу, он может сократить набор тестовых случаев.
Сокращение количества тестов — очень важная часть процесса тестирования программного обеспечения.
Тестирование программного обеспечения во многом зависит от сокращения количества тестовых случаев, и при таком подходе достигается максимальное покрытие тестированием и избежание избыточности.
Цель тестировщиков программного обеспечения — охватить продукт с помощью эффективных тестовых примеров, проверяющих все возможные комбинации действий.
Тестировщики могут добиться успеха с минимальными усилиями, используя подходы (алгоритмы) дискретной математики для поиска оптимального набора тестовых примеров и максимизации эффективности процесса тестирования программного обеспечения.
Дискретная математика также помогает нам понять, как на самом деле создается программное обеспечение, поскольку все программы используют алгоритмы и методы дискретной математики и математической логики.
Поэтому, если мы поймем, как это работает, мы сможем найти в программе ошибки или проблемы, которые не могут быть обнаружены со стороны пользователя.
Сети Петри
Давайте рассмотрим пример того, как приложение работает на микросервисной технологии с использованием сетей Петри (динамический граф):
Здесь мы видим, что система имеет начальное состояние и ей необходимо получить некий сигнал, который отправляется от другого сервиса (появляется токен).
В зависимости от полученного результата следует выполнить следующие действия.
Таким образом, сеть Петри иллюстрирует динамику всей системы.
Если какая-либо проблема существует, мы сможем быстрее изолировать дефект.
Нейронные сети
Искусственные нейронные сети также основаны на принципах графов.Они имитируют возможности обработки информации нейронами человеческого мозга.
Каждая часть нейронной системы основана на графе, который содержит «входные» узлы, «скрытый» слой и «выходные» узлы.

Некоторые данные поступают на входной слой, а алгоритмы скрытого слоя обрабатывают эти данные и отправляют результат на выходной этап.
Таким образом, нейронная сеть может выполнять действия на основе этих данных.
Нейронные сети также состоят из множества похожих графов с разной логикой, поэтому они могут принимать решения на основе входных параметров.
Миллениум Тестирование
Наш последний пример использования дискретной математики в тестировании включает в себя построение процесса тестирования программного обеспечения.В настоящее время существует множество методологий и подходов, получивших название «тестирование тысячелетия», которые были разработаны задолго до их фактического использования, начиная с 2000-х годов, когда разработка программного обеспечения начала стремительно развиваться.
BDD (Behavior Driven Development) — часть так называемого тестирования Millennium, эта методология является расширением TDD (Test Driven Development).
BDD позволяет тестировщикам установить более тесную связь между критериями приемлемости для данной функции и тестами, используемыми для проверки этой функциональности.
BDD может преобразовывать структурированные операторы естественного языка в исполняемые тесты, тем самым обеспечивая большую ясность и понимание для сторон бизнеса и разработчиков, поскольку они начинают говорить на одном и том же общем языке.
Базовая структура рабочего процесса BDD также основана на динамическом графе (сеть Петри).
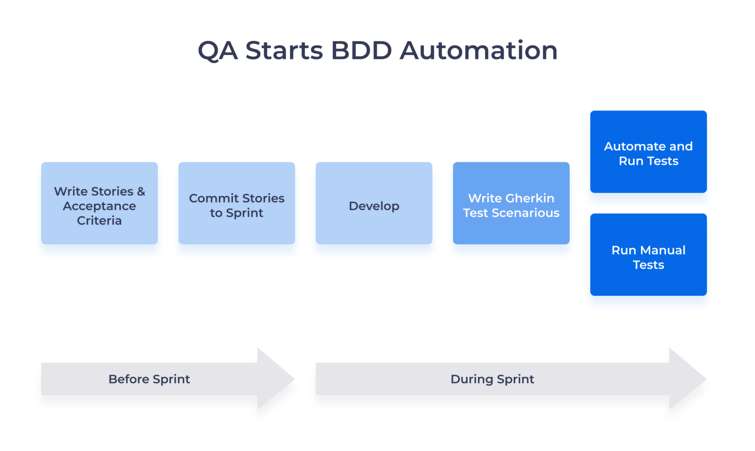
Как видно из этой структуры, за каждым процессом следует другой процесс, и он не может перейти к следующему этапу, пока не будет завершен предыдущий этап.
И снова принципы дискретной математики помогают нам более эффективно понять этот процесс.
В заключение хотелось бы еще раз перечислить преимущества использования дискретной математики в процессе разработки программного обеспечения:
- Помощь в понимании бизнес-логики необходимого функционала
- Упрощается разбиение сложных задач на более простые
- Предоставление профессионалам возможности проводить эффективное тестирование с меньшими усилиями
- Помощь в понимании и визуализации структуры всего, что мы хотим
Каждый аспект дискретной математики может помочь разработчикам понять общий порядок работы программного обеспечения и его принципы на протяжении всего жизненного цикла разработки программного обеспечения.
Теги: #qa #тестирование ИТ-систем #тестирование

-
Антигуа И Барбуда
19 Oct, 24 -
Ресурсы Яндекса Не Отвечают В 17:13 Мск
19 Oct, 24 -
Инициатива Fruct – Общее Описание
19 Oct, 24


