В предыдущая статья рассмотрена реализация самой кривой Ed25519, операции сложения и умножения на число, восстановление второй координаты.
В этой статье рассматривается, как эффективно использовать эти операции для электронной подписи сообщений и работы в I2P.
Алгоритм подписи EdDSA
В отличие от RSA, где закрытый и открытый ключ могут использоваться напрямую, здесь приходится использовать более сложную схему и вводить некоторый дополнительный объект. EdDSA концептуально реализует алгоритм ДПО , распространив его на случай кривых.Подпись представляет собой пару чисел (R, S), для EdDSA длина каждого составляет 32 байта, общая длина подписи — 64 байта.
Подписываются не сами данные, а их хеш.
В качестве хэш-функции используется SHA512. Далее маленькими буквами будут обозначаться цифры, а большими — соответствующая точка кривой, полученной умножением числа на базовую точку В.
Пусть h — хеш подписываемого сообщения, a — секретный ключ, а A — соответствующий открытый ключ (A = a*B).
Давайте возьмем случайное число r и посчитаем R = r*B и s = r+h*a. Пара (R,s) будет подписью, где R представлен координатой y. При проверке подписи получатель знает A и h и ему необходимо проверить истинность (R,s).
Для этого проверяется равенство: s*B = R+h*A.
Действительно (r+h*a)*B = r*B+h*a*B = R+h*A. 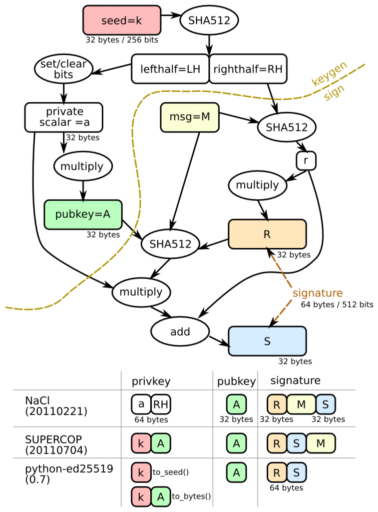
Обратите внимание, что s вычисляется непосредственно на основе секретного ключа, а не сгенерированной им точки, поэтому ошибки в реализации могут привести к его немедленной компрометации.
В частности, неудачный выбор р.
Чтобы избежать этого, Бернштейн предлагает вычислять r как хеш половины хеша секретного ключа, объединенного с подписываемыми данными, но выбор r каким-либо другим способом не нарушит алгоритм, то есть сами значения подписи будут другими, но результат проверки будет тот же.
Будем вычислять r, как предлагает Бернштейн и как это сделано в официальном I2P.
Ээффективная реализация умножения
Для дальнейших расчетов понадобится ранее неиспользованный параметр кривой l=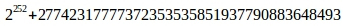
, такой, что l*B=0. Из этого равенства сразу следует, что значение множителя перед точкой не должно превышать l, иначе это приведет лишь к увеличению объема вычислений.
Если множитель превышает l, то его нужно брать по модулю, в частности значение h, которое представляет собой 64-байтовый хэш SHA512. Отсюда, в свою очередь, следует, что множитель в операции умножения не превышает 32 байт и старший бит всегда равен нулю.
Как видно из формул, для подписи требуется одно умножение на базовую точку, а для проверки подписи необходимо два умножения: одно на базовую точку, а второе на открытый ключ.
Для базовой точки имеет смысл заранее рассчитать результат умножения на разные коэффициенты.
Самым простым является ряд (В, 2*В, 4*В, 8*В, .
) общим числом 255 точек, что позволяет исключить операцию удвоения на каждом шаге.
Можно пойти дальше и разложить множитель не по степени двойки, а по степени 16, и на каждые 4 бита множителя добавить к результату расчетную точку из массива.
Для этого вам потребуется посчитать и сохранить 32*2*16 точек, но делается это один раз за время всей работы.
Таким образом, умножение на B сокращается ровно до 64 сложений и подписание сообщения осуществляется быстро.
Вот как это выглядит в коде.
Теги: #C++ #i2p #Ed25519 #Криптография #программирование #i2pEDDSAPoint res {zero, one}; for (int i = 0; i < 32; i++) {

-
Разговор Уолдена
19 Oct, 24 -
Определение Молекулярной Весы
19 Oct, 24 -
Обучение Слепому Подписанию
19 Oct, 24 -
Первый Опыт: Mac Mini На M1
19 Oct, 24


