На днях прочитал интересную статья о рейтингах.
Не рекомендую использовать ее в качестве практического руководства (почему смотрите в комментариях к ней), однако прочитать ее было интересно и натолкнуло на одну идею.
Допустим, у нас есть рейтинг от 1 до 5. Причем некоторые рейтинги завышены, некоторые пользователи выставляют их случайным образом.
Как отфильтровать зерна от плевел? Если построить диаграмму количества людей, поставивших определенный рейтинг, то можно примерно увидеть, на сколько голосов было увеличено.
Надо, конечно, сравнивать с другими диаграммами, но из этой картинки видно, что некоторые из «пятерок» напортачили: 
В общем, человек может определить разметку по схеме, а значит, и машина тоже.
Распределение голосов можно описать функция бета-распределения .
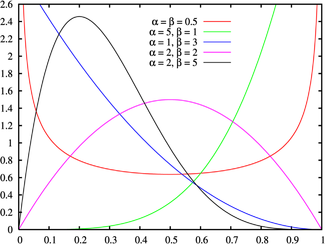
Если в большинстве случаев голосование можно описать бета-функцией, а в некоторых случаях нет, то часть голосов можно удалить.
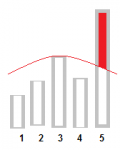
Таким образом мы исключим не все плохие голоса, мы исключим некоторые хорошие.
Для статей с небольшим количеством голосов такие манипуляции недопустимы.
Бета-распределение имеет два параметра: альфа и бета.
Еще у нас есть два параметра: средний балл (E) и дисперсия (D) — мера дисперсии.
Из Википедии это известно.
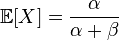
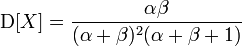
Теперь решим систему уравнений.
Это долго и утомительно.
Е=а/(а+b) d=ab/((a+b)^2 * (a+b+1)) замените a/(a+b) на E d=bE/((a+b) * (a+b+1)) замените 1/(a+b) на E/a d=b*E^2/(a * (a+b+1)) умножьте обе части на (a * (a+b+1)) d(а * (а+b+1))=b*E^2 раскрой скобки и поменяй местами b*E^2=да^2 + даб + да вычесть мазок с обеих сторон б*E^2-даб=да^2 + да б(Е^2-да)=да(а+1) б=да(а+1)/(Е^2-да) Вернемся к первому уравнению E=a/(a+b)=> (a+b)=a/E=> b=a/E -a давайте объединим оба уравнения б=а/Е -а=да(а+1)/(Е^2-да) а/Е -а=да(а+1)/(Е^2-да) разделить на 1/E -1=d(a+1)/(E^2-da) умножить на E(E^2-da) (1-E)(E^2-da)=Ed(a+1) Е^2-да -Е^3 + Эда=Еда + Эд Эда сжимается E^2-да -E^3 = Эд E^2 -E^3 -Ed =da а= (Е^2 -Е^3 -Ed)/d b=a/E -a=a(1/E-1)=a(1-E)/E=(E^2 -E^3 -Ed)(1-E)/Ed=(E -E^ 2 -d)(1-E)/d=(E -E^2 -d - E^2 + E^3 +dE)/d б=(Е^3-2Е^2+Е)/d +Е -1Со временем мы сможем создать бета-функцию.
Все рейтинги выше этого, скорее всего, являются мошенничеством.
Если кому интересно, напишу подробнее.
Теги: #рейтинг #чит #математика #Алгоритмы #Разработка сайтов #Алгоритмы #математика

-
Что Такое Облачный Веб-Хостинг?
19 Oct, 24 -
Был Введен Scrum, А Agile Забыли
19 Oct, 24 -
Как Делают Вакцины?
19 Oct, 24 -
Кланяемся Ниже!
19 Oct, 24


