О чем мы говорим? В этом посте я хотел бы описать часть системы времени выполнения (RTS — RunTime System здесь и далее) компилятора.
ДВМХ .
Рассматриваемая часть, как видно из названия, относится к обработке пользовательских массивов на GPU, а именно к их автоматическому преобразованию или реорганизации в памяти ускорителя.
Эти преобразования производятся для эффективного доступа к памяти графического процессора в ходе вычислительных циклов.
Что такое DVMH, как можно адаптироваться к расчетам и почему это делается автоматически, описано ниже.
Что такое ДВМХ Поскольку данный пост посвящен обзору алгоритмов преобразования массивов, я лишь кратко опишу, что такое DVMH, поскольку он понадобится для описания принципов работы.
Начать нужно с системы DVM (Distribute Virtual Memory) — системы, которая предназначена для разработки программ для кластеров, содержащих ускорители (Nvidia GPU и Intel Xeon Phi) и многоядерные процессоры в узлах.
С помощью этой системы можно легко распараллелить большие последовательные программы, работающие преимущественно со структурными сетками или структурными типами данных, а также легко сопоставить программу с кластером, узлы которого могут содержать устройства различной архитектуры.
В состав системы DVM входят:
- Компиляторы с языков программирования C (а в будущем и C++, конечно с некоторыми ограничениями) и Fortran — C-DVMH и Fortran-DVMH. Языки и компиляторы мы будем вообще называть DVMH. DVMH — это расширение рассматриваемых языков программирования прагмами или специальными комментариями, невидимыми стандартным компиляторам (по аналогии, например, с OpenMP, OpenACC).
Таким образом, программисту нужно разместить лишь небольшое количество директив, указывающих, как распределяются данные и как вычисления сопоставляются с распределенными данными в вычислительных циклах.
После этого пользователь получает как последовательную программу, так и параллельную.
Полученную программу можно выполнять на кластере на разном количестве узлов, на одном или нескольких графических процессорах внутри одного узла, а также, например, использовать сразу многоядерные процессоры, графические ускорители и ускорители Intel Xeon Phi (если все это присутствует на рассматриваемом сервере).
Более подробную информацию можно найти здесь;
- Библиотека поддержки Lib-DVMH или система времени выполнения RTSH (H означает гетерогенный — буква в названиях многих компонентов, появившаяся после того, как система была расширена для поддержки графических процессоров и Xeon Phi).
С помощью этой системы осуществляются все настройки пользовательской программы во время ее работы;
- Инструменты отладки и инструменты для отладки эффективности программ DVMH (пока только для программ Fortran-DVMH).
Компиляторы DVMH транслируют полученную программу с помощью директив DVMH в программу, используя вызовы MPI, OpenMP, CUDA и RTSH. Таким образом, пользовательскую программу можно легко распараллелить с помощью директив распределения вычислений (почти аналогичных OpenMP или OpenACC) и директив распределения данных.
Более того, данная программа продолжает оставаться последовательной, что важно для ее дальнейшего развития и поддержки.
Написать «хорошую» последовательную программу и разместить в такой программе директивы для DVMH-компилятора все же проще, чем заниматься распараллеливанием вручную.
Уровни параллелизма После краткого вступления и введения в дело давайте посмотрим, как исходная программа (а именно вычислительные циклы) отображается на разные уровни параллелизма внутри RTSH. В настоящее время для достижения высокой вычислительной мощности используют большое количество потоков внутри одного устройства вместо увеличения частоты каждого потока.
Это в свою очередь приводит к необходимости изучения не только стандарта (разумеется, MPI) взаимодействия процессов между узлами, но и к появлению гетерогенных архитектур, а вместе с ними и различных параллельных языков, как высокого уровня, так и низкого.
И все это усложняет жизнь конечному потребителю.
А для достижения высокой производительности приложений необходимо использовать все возможности конкретного вычислительного кластера.
На этом этапе мы можем представить себе два уровня параллелизма — между узлами и внутри узла.
В узле можно использовать один или несколько графических процессоров, а также многоядерные процессоры.
Intel Xeon Phi в этой схеме рассматривается как отдельный узел, содержащий многоядерный процессор.
Ниже представлена обобщенная схема вычислительного кластера, на который могут быть отображены программы DVMH: 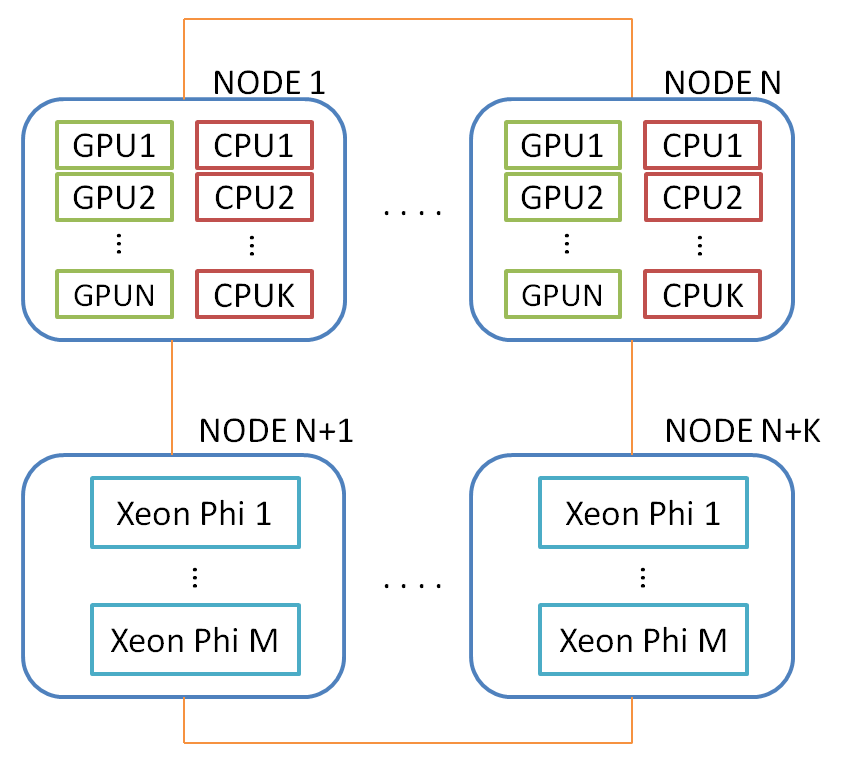
Естественно, возникает вопрос о балансировке нагрузки устройств (механизм которого есть в DVMH), но это выходит за рамки данного поста.
Все дальнейшие соображения будут касаться одного графического процессора в пределах одного узла.
Описанные ниже преобразования выполняются на всех графических процессорах, на которых работает программа DVMH, независимо.
Почему необходима реорганизация данных? Наконец, после пространного вступления, мы подходим к вопросу о самой реорганизации.
Для чего все это? Но для чего? Рассмотрим некоторый вычислительный цикл:
У нас есть четырехмерный массив, где первое (самое быстрое) измерение, например, содержит 5 физических величин, а остальные — координаты в пространстве расчетной области.double ARRAY[Z][Y][X][5]; for(int I = 1; i < Z; ++I) for(int J = 1; J < Y; ++J) for(int K = 1; K < X; ++K) ARRAY[K][J][I][4] = Func(ARRAY[K][J][I][2], ARRAY[K][J][I][5]);
В программе массив был объявлен так, чтобы первое (близко расположенное в памяти) измерение состояло из этих 5 элементов, чтобы кэш процессора хорошо работал в вычислительных циклах.
В этом примере вам необходимо получить доступ к элементам быстрого измерения 2, 4 и 5 на каждой итерации трех циклов.
Также стоит отметить, что в этом измерении нет цикла.
А из-за, например, разной природы этих величин, будут отличаться и расчеты для каждого из 5 элементов.
Таким образом, можно параллельно выполнять циклы по I, J, K. В этом примере каждый элемент массива ARRAY каким-то образом будет сопоставлен с параллельным циклом, например так: #pragma dvm array distribute[block][block][block][*]
double ARRAY[Z][Y][X][5];
#pragma dvm parallel([I][J][K] on ARRAY[I][J][K][*])
for(int I = 1; i < Z; ++I)
for(int J = 1; J < Y; ++J)
for(int K = 1; K < X; ++K)
ARRAY[K][J][I][4] = Func(ARRAY[K][J][I][2], ARRAY[K][J][I][5]);
То есть появляется распределение данных, по которому распределяются расчеты.
Приведенные выше директивы DVMH говорят, что массив должен быть распределен по трем измерениям равными блоками, а четвертый (самый быстрый) должен быть умножен.
Эта запись позволяет вам сопоставить массив с сеткой процессора, указанной при запуске программы DVMH. Следующая директива говорит, что необходимо выполнить ход (I,J,K) в соответствии с правилом распределения массива ARRAY. Таким образом, директива PARALLEL определяет отображение итераций цикла на элементы массива.
Во время выполнения RTSH знает, как устроены массивы и как должны быть организованы вычисления.
Данный цикл, а именно все пространство витков, может быть отображен как в поток OpenMP, так и в поток CUDA, поскольку все три цикла не имеют никаких зависимостей.
Мы заинтересованы в преобразовании в архитектуру CUDA. Всем известно, что блок CUDA содержит три измерения — x, y, z. Самый первый – самый быстрый.
Быстрое измерение отображается на деформациях блока CUDA. Почему обо всем этом нужно упоминать? Потому что глобальная память графического процессора (GDDR5) является узким местом в любых вычислениях.
А память устроена так, что максимально быстрый доступ осуществляется по одному варпу только в том случае, если все загруженные элементы находятся подряд. Для приведенного выше цикла существует 6 вариантов сопоставления пространства катушек (I,J,K) с блоком CUDA (x, y, z), но ни один из них не обеспечивает эффективный доступ к массиву ARRAY. Что является причиной этого? Если посмотреть описание массива, то можно увидеть, что первое измерение содержит 5 элементов и циклов по нему нет. Таким образом, элементы второго быстрого измерения лежат на расстоянии 40 байт (5 элементов типа double), что приводит к увеличению количества транзакций к памяти GPU (вместо 1 транзакции один варп может составлять до 32 транзакции).
Все это приводит к перегрузке шины памяти и снижению производительности.
Для решения задачи в данном случае достаточно поменять местами первое и второе измерения, то есть транспонировать двумерную матрицу размера X*5 Y*Z раз или выполнить независимые транспонирования Y*Z. Но что значит поменять местами размеры массива? Могут возникнуть следующие проблемы:
- В код необходимо добавить дополнительные циклы, выполняющие это преобразование;
- Если вы переставите размерности в программном коде, вам придется исправлять всю программу, так как расчеты во всех циклах станут неверными, если вы переставите размерности массива в одном месте программы.
А если программа большая, то можно допустить много ошибок;
- Неясно, какой эффект будет получен от перегруппировки и как перегруппировка повлияет на следующий цикл.
Вполне возможно, что потребуется новая перестановка или возврат массива в исходное состояние;
- Создайте две версии программы, поскольку этот цикл больше не будет эффективно выполняться на ЦП.
Прежде чем рассматривать типы трансформаций и их реализацию на CUDA, перечислю некоторые неоспоримые преимущества нашего подхода:
- У пользователя есть одна DVMH-программа, он занимается написанием алгоритма;
- Этот режим можно включить во время компиляции программы DVMH, указав всего одну опцию компилятору DVMH -autoTfm. Таким образом, пользователь может попробовать оба режима без каких-либо изменений программы и оценить ускорение;
- Это преобразование выполняется в режиме по требованию.
Это означает, что если перед вычислительным циклом изменить порядок размерностей массива, то обратная перестановка после вычислений производиться не будет, так как вполне возможно, что для следующего цикла такое расположение массива будет выгодным;
- Значительное ускорение работы программы (до 6 раз) по сравнению с той же программой, выполненной без использования этой опции.
1. Поменяйте местами размеры массива, которые физически смежны.
Описанный выше пример подходит для такого типа трансформации.
В этом случае необходимо транспонировать двумерную плоскость, которая может располагаться на любых соседних двух измерениях массива.
Если необходимо транспонировать первые два измерения, то подойдет хорошо описанный алгоритм транспонирования матриц с использованием разделяемой памяти: __shared__ T temp[BLOCK_DIM][BLOCK_DIM + 1];
CudaSizeType x1Index = (blockIdx.x + pX) * blockDim.x + threadIdx.x;
CudaSizeType y1Index = (blockIdx.y + pY) * blockDim.y + threadIdx.y;
CudaSizeType x2Index = (blockIdx.y + pY) * blockDim.y + threadIdx.x;
CudaSizeType y2Index = (blockIdx.x + pX) * blockDim.x + threadIdx.y;
CudaSizeType zIndex = blockIdx.z + pZ;
CudaSizeType zAdd = zIndex * dimX * dimY;
CudaSizeType idx1 = x1Index + y1Index * dimX + zAdd;
CudaSizeType idx2 = x2Index + y2Index * dimY + zAdd;
if ((x1Index < dimX) && (y1Index < dimY)) {
temp[threadIdx.y][threadIdx.x] = inputMatrix[idx1];
}
__syncthreads();
if ((x2Index < dimY) && (y2Index < dimX)) {
outputMatrix[idx2] = temp[threadIdx.x][threadIdx.y];
}
В случае с квадратной матрицей можно выполнить так называемую транспозицию «на месте», для которой не нужно выделять дополнительную память на GPU.
2. Поменяйте местами измерения массива, которые физически не являются соседними.
Этот тип включает в себя перестановки любых двух измерений массива.
Стоит различать два типа таких перестановок: первый – это изменение любого измерения первым и изменение любых измерений друг с другом, причем ни один из них не является первым (самым быстрым).
Это разделение должно быть четким, поскольку элементы самого быстрого измерения лежат в ряд и доступ к ним также должен быть возможен в ряд. Для этого можно использовать общую память: __shared__ T temp[BLOCK_DIM][BLOCK_DIM + 1];
CudaSizeType x1Index = (blockIdx.x + pX) * blockDim.x + threadIdx.x;
CudaSizeType y1Index = (blockIdx.y + pY) * blockDim.y + threadIdx.y;
CudaSizeType x2Index = (blockIdx.y + pY) * blockDim.y + threadIdx.x;
CudaSizeType y2Index = (blockIdx.x + pX) * blockDim.x + threadIdx.y;
CudaSizeType zIndex = blockIdx.z + pZ;
CudaSizeType zAdd = zIndex * dimX * dimB * dimY;
CudaSizeType idx1 = x1Index + y1Index * dimX * dimB + zAdd;
CudaSizeType idx2 = x2Index + y2Index * dimY * dimB + zAdd;
for (CudaSizeType k = 0; k < dimB; k++) {
if (k > 0)
__syncthreads();
if ((x1Index < dimX) && (y1Index < dimY)) {
temp[threadIdx.y][threadIdx.x] = inputMatrix[idx1 + k * dimX];
}
__syncthreads();
if ((x2Index < dimY) && (y2Index < dimX)) {
outputMatrix[idx2 + k * dimY] = temp[threadIdx.x][threadIdx.y];
}
}
Если вам нужно поменять местами какие-либо другие измерения между собой, то разделяемая память не нужна, так как доступ к быстрому измерению массива будет осуществляться «корректно» (соседние потоки будут работать с соседними ячейками в памяти GPU).
3. Диагонализировать массив.
Этот тип перестановки нестандартен и необходим для параллельного выполнения циклов с регулярной зависимостью данных.
Эта перестановка обеспечивает «правильный» доступ при обработке цикла, имеющего зависимости.
Давайте посмотрим на пример такого цикла: #pragma dvm parallel([ii][j][i] on A[i][j][ii]) across(A[1:1][1:1][1:1])
for (ii = 1; ii < K - 1; ii++)
for (j = 1; j < M - 1; j++)
for (i = 1; i < N - 1; i++)
A[i][j][ii] = A[i + 1][j][ii] + A[i][j + 1][ii] + A[i][j][ii + 1] + A[i - 1][j][ii] + A[i][j - 1][ii] + A[i][j][ii - 1];
В этом случае имеется зависимость по всем трем измерениям цикла или трем измерениям массива A. Чтобы сообщить DVMH-компилятору о наличии в этом цикле регулярной зависимости (зависимые элементы можно выразить формулой a* x + b, где a и b — константы), существует спецификация ACROSS. В этом цикле существует прямая и обратная зависимость.
Пространство поворотов этого цикла образовано параллелепипедом (а в частном случае — трехмерным кубом).
Плоскости этого параллелепипеда, повернутого на 45 градусов относительно каждой грани, можно выполнить параллельно, а сами плоскости - последовательно.
Благодаря этому появляется доступ к двуугольным элементам первых двух быстрых измерений массива А.
А для увеличения производительности графического процессора необходимо выполнить диагональное преобразование массива.
В простом случае преобразование одной плоскости выглядит так: 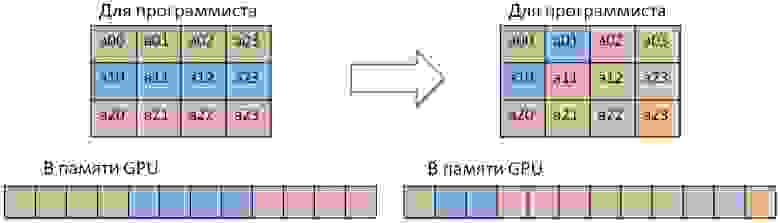
Это преобразование может быть выполнено так же быстро, как и транспонирование матрицы.
Для этого вам нужно использовать общую память.
Только, в отличие от транспонирования матрицы, обрабатываемый блок будет не квадратным, а в виде параллелограмма, чтобы эффективно использовать пропускную способность памяти GPU при чтении и записи (при диагонализации показывается только первая полоска, так как все остальные делятся таким же образом): 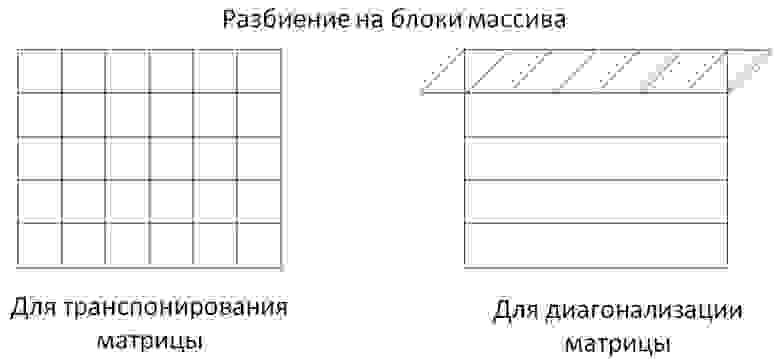
Реализованы следующие виды диагонализации (Rx и Ry — размеры диагонализированного прямоугольника):
- Параллельно боковой диагонали и Rx == Ry;
- Параллельно вторичной диагонали и Rx < Ry;
- Параллельно вторичной диагонали и Rx > Ry;
- Параллельно главной диагонали и Rx == Ry;
- Параллельно главной диагонали и Rx < Ry;
- Параллельно главной диагонали и Rx > Ry.
__shared__ T data[BLOCK_DIM][BLOCK_DIM + 1];
__shared__ IndexType sharedIdx[BLOCK_DIM][BLOCK_DIM + 1];
__shared__ bool conditions[BLOCK_DIM][BLOCK_DIM + 1];
bool condition;
IndexType shift;
int revX, revY;
if (slash == 0) {
shift = -threadIdx.y;
revX = BLOCK_DIM - 1 - threadIdx.x;
revY = BLOCK_DIM - 1 - threadIdx.y;
} else {
shift = threadIdx.y - BLOCK_DIM;
revX = threadIdx.x;
revY = threadIdx.y;
}
IndexType x = (IndexType)blockIdx.x * blockDim.x + threadIdx.x + shift;
IndexType y = (IndexType)blockIdx.y * blockDim.y + threadIdx.y;
IndexType z = (IndexType)blockIdx.z * blockDim.z + threadIdx.z;
dvmh_convert_XY<IndexType, slash, cmp_X_Y>(x, y, Rx, Ry, sharedIdx[threadIdx.y][threadIdx.x]);
condition = (0 <= x && 0 <= y && x < Rx && y < Ry);
conditions[threadIdx.y][threadIdx.x] = condition;
if (back == 1)
__syncthreads();
#pragma unroll
for (int zz = z; zz < z + manyZ; ++zz) {
IndexType normIdx = x + Rx * (y + Ry * zz);
if (back == 0) {
if (condition && zz < Rz)
data[threadIdx.y][threadIdx.x] = src[normIdx];
__syncthreads();
if (conditions[revX][revY] && zz < Rz)
dst[sharedIdx[revX][revY] + zz * Rx * Ry] = data[revX][revY];
} else {
if (conditions[revX][revY] && zz < Rz)
data[revX][revY] = src[sharedIdx[revX][revY] + zz * Rx * Ry];
__syncthreads();
if (condition && zz < Rz)
dst[normIdx] = data[threadIdx.y][threadIdx.x];
}
}
В этом случае необходимо передать значение условия и вычисленную координату в диагональном представлении с помощью dvmh_convert_XY в другие потоки, поскольку в отличие от транспозиции не удается однозначно вычислить обе координаты (откуда читать и куда писать).
Нижняя граница.
Какие перестановки были реализованы:
- Перестановка двух соседних измерений массива;
- Перестановка двух несмежных измерений массива;
- Оцифровка двух соседних самых быстрых измерений массива;
- [Запланировано] Оцифровка любых двух самых быстрых измерений массива (диагонализуемое измерение становится самым быстрым);
- Копирование разреза из диагонализированного массива (например, для обновления «теневых» ребер в случае вычислений на нескольких графических процессорах);
Все тесты проводились на графическом процессоре GTX Titan, Nvidia CUDA ToolKit 7.0 и процессоре Intel Xeon E5 1660 v2 с компилятором Intel версии 15. Все реализованные преобразования будем сравнивать с ядром обычного копирования, поскольку реорганизация массива — это копирование одного участка памяти в другой по определенному правилу.
Ядро копирования выглядит так: __global__ void copyGPU(const double *src, double *dist, unsigned elems)
{
Теги: #nvidia #gpu #DVMH #реорганизация #трансформация #транспозиция #Высокая производительность #C++ #Алгоритмы #GPGPU #Параллельное программирование

-
Серьезно, Игры?
19 Oct, 24 -
Аномалия Франго, Сюжет
19 Oct, 24 -
Об Одной Девушке
19 Oct, 24 -
E-Gold Прилег Отдохнуть...
19 Oct, 24


