Предыстория и введение Как уже описано в предыдущем статья , в процессе переделки игрушки-осциллографа DSO138 возникла идея в DSO303 попробовать трюк с удвоением частоты дискретизации.
Фактически для STM32F303 теоретически максимально достижимая частота дискретизации с точки зрения входа АЦП, а это определяется минимальным временем открытия АЦП, которое в нашем случае составляет 1,5 такта х (1/72 МГц).
), или примерно 20,8 наносекунд, что дает 48 MSPS (миллионов выборок в секунду).
Однако при параллельной работе 4 АЦП на частоте 6 МГц можно достичь только 24 MSPS из-за ограниченной скорости АЦП.
Представим, что мы рассматриваем регулярно периодический сигнал, который к тому же является постоянным, т.е.
не испытывает колебаний частоты и амплитуды во времени.
Можно ли как-то оцифровать его не за один, а за несколько проходов, повысив тем самым эффективную частоту дискретизации?
Оцифровка в три прохода – идея
Обратимся к рис.1, который собственно и демонстрирует идею многопроходной оцифровки.
Предположим, что каждый АЦП запускается своим сигналом таймера, который работает на удвоенной тактовой частоте микроконтроллера и АЦП (для 32F303 - 72 и 144 МГц соответственно).
В этом случае цикл оцифровки занимает 12 тактов АЦП (24 такта таймера) с разрешением 10 бит. Разделим этот цикл на 8 слотов по 3 такта таймера (1,5 такта АЦП), что в точности соответствует времени открытия УВХ.
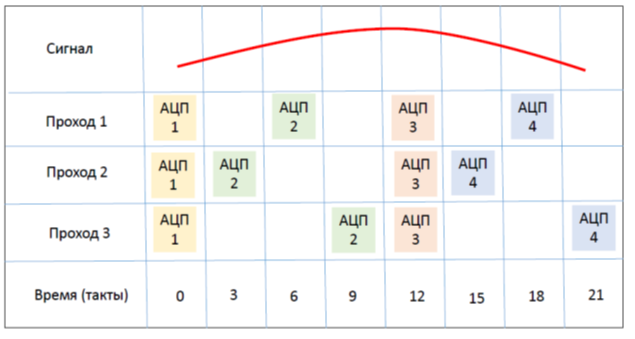
Рисунок 1. Идея многопроходной оцифровки.
Мы сделаем каналы АЦП 1 и АЦП 3 опорными, они всегда будут срабатывать в одно и то же время в цикле, а время отклика каналов АЦП 2 и АЦП 4 будет перемещаться внутри цикла в зависимости от прохода.
Вот и все, выполнив 3 прохода такой оцифровки мы получим окончательный результат. «Однако, — скажет внимательный читатель, — но извините, а почему вы предполагаете, что ваш цикл оцифровки в следующем проходе будет находиться в постоянном положении относительно сигнала? Ведь начало процесса оцифровки происходит в случайный момент времени.
» И, конечно, он будет абсолютно прав.
Но для этого у нас есть два опорных канала из четырех доступных, и время прогонять процесс оцифровки неограниченное количество раз.
Просто нужно прогнать следующий проход много раз до того момента, пока положение цикла оцифровки относительно сигнала не станет достаточно близким к тому, что было во время первого прохода, проверяя корреляцию по опорным каналам.
Таким образом, наш процесс оцифровки будет выглядеть так:
- Оцифрованные и записанные данные с прохода 1;
- Оцифрованные данные из Пассажа 2;
- Мы рассчитали корреляцию опорных каналов, если она достаточно хорошая, то записали данные Pass 2, если нет, то повторяем шаг 2;
- Оцифрованные данные из Пассажа 3;
- Рассчитали корреляцию, если все хорошо, то записали данные и приступили к окончательной сборке и обработке данных оцифровки и отображению полученного изображения, если нет, то повторяем оцифровку Пассажа 3.
Полученные результаты
Да, в результате иногда процесс занимает довольно много времени, и оцифровку можно повторить десятки тысяч раз, прежде чем будет достигнут результат; Да, этот метод подходит не для всех сигналов; Да, результат не без искусственных артефактов, как на рис.2., но довольно часто получается как на рис.
3. На обоих рисунках на вход подается прямоугольный сигнал частотой 1 МГц.
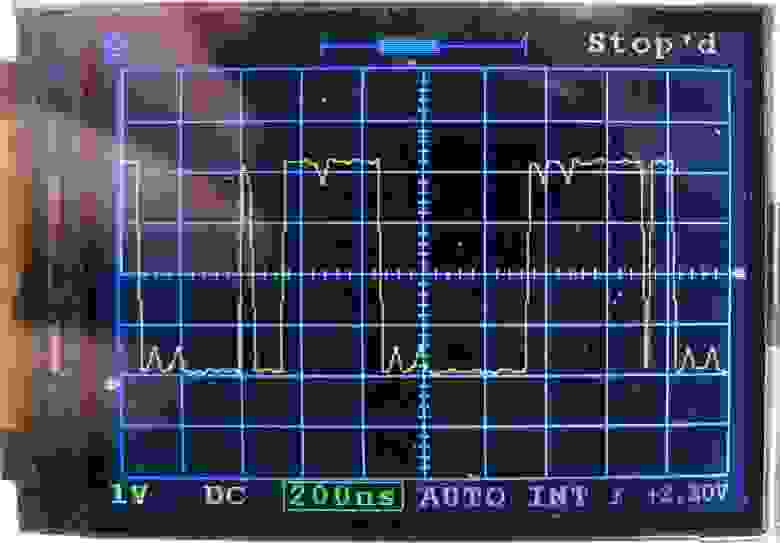
Рис.
2. Результат трехпроходной оцифровки.
Есть артефакты.
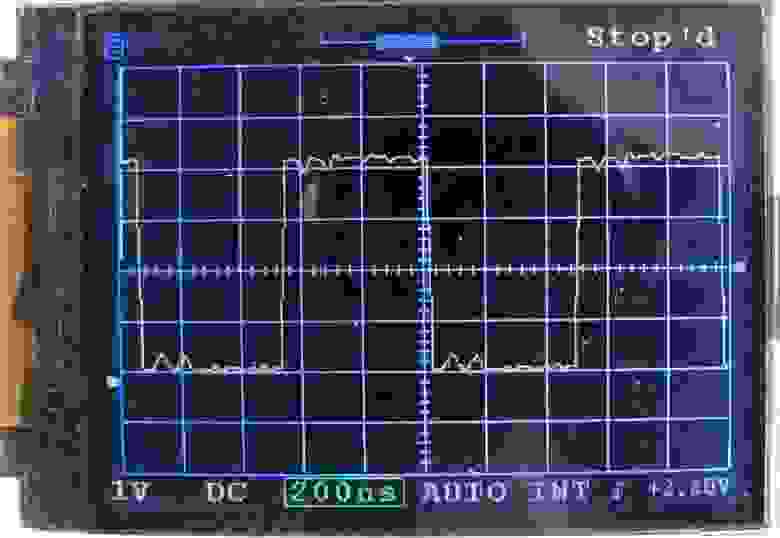
Рис.
3. Результат трехпроходной оцифровки.
Прямоугольная волна 1 МГц.
При этом худшие результаты получаются для сигналов с быстрым изменением формы и острыми краями (меандр), а лучшие результаты наблюдаются для плавных сигналов (синусоида).
Для иллюстрации на рис.
4 также представлена картина синусоидального сигнала частотой 200 кГц.
Сигнал там «немного» зашумленный, с небольшими помехами, что сразу приводит, к сожалению, к достаточно большим искажениям в виде такой вот своеобразной «бороды», поскольку одно из условий правильной картинки при таком способе оцифровки, который как уже упоминалось выше, – это постоянство и отсутствие колебаний сигнала во времени, что и иллюстрирует эта картинка.

Рис.
4. Синусоидальный сигнал частотой 200 кГц.
Период сигнала для корректной работы корреляционного алгоритма теоретически не может быть меньше цикла оцифровки; практически приемлемый результат получается только при периодах сигнала более 3 циклов, т.е.
> 500 наносекунд. Таким образом, к сожалению, рассматривать сигналы с частотами более 2 МГц все равно не удастся.
Но по крайней мере такие сигналы можно увидеть достаточно подробно, что, несомненно, будет полезно.
Именно так DSO303 получил время развертки 500 и 200 наносекунд на ячейку.
В режиме 500 наносекунд на ячейку изображение представляет собой честный результат оцифровки, каждая точка = образец.
Потом я подумал, что неплохо бы и это изображение растянуть, так появился режим 200 наносекунд на ячейку.
Здесь используются точно те же данные, что и при сканировании по 500 наносекунд на ячейку, только они растянуты так, что один семпл = 3 точки на экране.
Это оказалось довольно удобно и получило свое право на жизнь.
Все вышесказанное является экспериментальной идеей.
Автор не претендует на полную функциональность данного экспериментального метода оцифровки и не несет ответственности за результат. Любые вопросы, комментарии и предложения приветствуются.
Теги: #Программирование микроконтроллеров #Алгоритмы #Сделай сам или Сделай сам #отладка #проектирование схем #удвоение частоты дискретизации #переделка DSO138 #DSO303

-
Блиц-Интерфейс Excel
19 Oct, 24 -
Acaces`12 — Летняя Школа Hipeac
19 Oct, 24 -
Игра В Слова
19 Oct, 24 -
Как Сделать Динамичный, Переливающийся Фон
19 Oct, 24


