После длительного перерыва продолжаем серию о графических вероятностных моделях ( часть 1 , часть 2 ).
Сегодня мы наконец перейдем от постановки задач к алгоритмам; мы поговорим о самом простом, но часто полезном алгоритме вывода на графах факторов — алгоритме передачи сообщений.
Или, как его еще можно назвать, алгоритм правильной расстановки скобок.
Пример
И начнем сразу с конкретного примера – предположим, что вам нужно вычислить выражение
Здесь, формально говоря, четыре слагаемых, каждое из трёх множителей, всего три сложения и восемь умножений.
Проявим чудеса изобретательности и заметим, что двойная сумма здесь разлагается на произведение двух одинарных сумм: 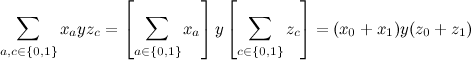
Вдруг останется только два сложения и два умножения — выгода очевидна.
Как вы, наверное, понимаете, если бы я не поленился написать сумму побольше, польза выросла бы в геометрической прогрессии — сворачиваем сумму экспоненциального числа слагаемых в произведение линейного числа маленьких скобок.
«Подумать только, бином Ньютона!» - скажут мне читатели; и они будут правы, это действительно очень похоже на бином Ньютона.
А внимательные читатели еще и удивятся, зачем вообще здесь понадобилась игра — ведь в данном примере она выглядит явно лишней.
Попробуем обобщить тот же пример — пусть теперь с нашими переменными вместо умножения происходит какая-то неизвестная функция: 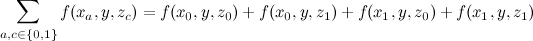
Работает ли тот же трюк, что и выше? Нет, не работает — мы не знаем никакой связи между разными значениями функции, для нас это черный ящик, и выносить из уравнения нечего; нам придется честно применить функцию четыре раза и сложить результаты.
Хитрость будет иметь место в промежуточном случае — мы все равно оставим в рассмотрении достаточно общую функцию, но теперь предположим, что ее можно разложить в произведение функции Икс И й и функции из й И я (окончательно й будет полностью вовлечен в дело): 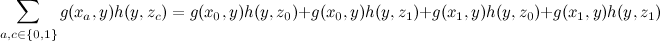
При такой постановке вопроса мы можем точно так же разложить большую сумму на произведение двух малых: 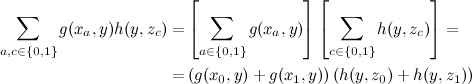
и существенно сэкономить на расчетах.
Заметим, что хотя мы и предполагали некоторую дополнительную структуру функции трех переменных, неверно, что переменные в ней Икс И я встречались совершенно независимо – их связывали через й , для чего по счастливому стечению обстоятельств нам не пришлось подводить итоги.
Кстати, обратите внимание, что результат этого суммирования является функцией й .
Какова мораль этого примера? Дело в том, что если нам нужно просуммировать большую функцию, и она разлагается в произведение меньших функций, то вполне возможно, что мы сможем найти удачное разложение в произведение скобок.
На пути к вероятностным моделям
.
но это ситуация вывода на графической вероятностной модели! Вспомните последовательную связь между переменными, которую мы обсуждали в Первый эпизод : 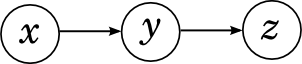
С вероятностной точки зрения это означает, что совместное распределение разлагается как 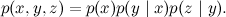
А это значит, что функция трех переменных Икс , й И я разложено в произведение функции Икс И й и функции из й И я , точно так же, как в нашем наивном примере.
И суммирование соответствует задаче маргинализация : используя заданную модель и, возможно, значения некоторых переменных, найти предельное распределение вероятностей 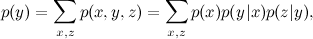
и теперь мы понимаем, что это выражение можно значительно упростить как 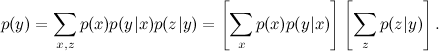
Задача маргинализации является основной для графических моделей, через нее формализуется все, о чем мы говорили.
последний раз : как обучать веса регрессии, как распознавать речь по готовой модели и как обучать модель распознавания на тестовых примерах, как найти рейтинги игроков после очередного турнира, как найти степень встречаемости тем в документах из корпус и так далее.
Факторные графы и цепные графы
Прелесть всего этого в том, что подобные рассуждения не нужно каждый раз придумывать заново, а можно обобщить.
Самое прямое обобщение относится к цепочке из нескольких событий, связанных последовательной связью: 
В этот момент будет удобно немного изменить картинку.
До сих пор мы рисовали только переменные, а функции (распределения вероятностей) подразумевали.
В частности, это означало факторизацию большой функции; например, картинка выше приводит к разложению 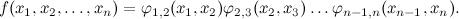
Давайте теперь выделим это явно: 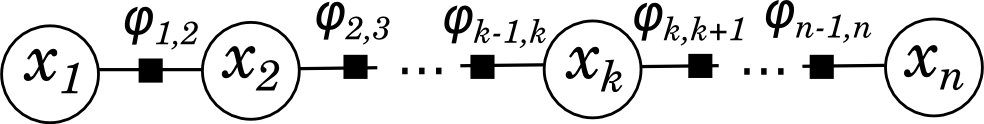
У нас есть двудольный граф, в котором два типа вершин соответствуют переменным и функциям.
Каждой функции сопоставлены переменные, от которых она зависит, а сам график задает разложение большой функции в произведение малых.
Эта конструкция называется Факторный график – обратите внимание, что это более общая конструкция, чем байесовская сеть убеждений, теперь вероятностное содержание пропало, и мы в принципе можем говорить о разложениях абстрактных функций (не обязательно распределений) в произведение меньших абстрактных функций (не обязательно условных распределений) ).
Теперь давайте применим наш трюк к проблеме относительной маргинализации.
Икс к .
Сначала вносим первую сумму, затем вторую, затем третью и так до тех пор, пока к -й; В результате получается более компактное представление левой части суммирования, которая к тому же не пересекается с правой частью (извините за длинную формулу, но здесь она гораздо понятнее слов): 
Вы можете сделать то же самое с правой стороной, и результат будет 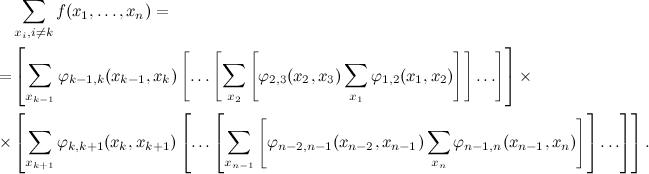
Обратите внимание, какой алгоритм расчета соответствует нашему трюку: начинаем с краев графа (с самых внутренних скобок) и постепенно идем к середине (точнее, к к th переменная), попутно сворачивая суммы.
Это можно рассматривать как передача сообщения от боковых сторон цепочки к середине.
На каждом шаге мы по сути делаем одно и то же — получаем результат предыдущих суммирований как функцию одной переменной.
час я ( Икс я ), а затем мы сворачиваем его следующим образом: 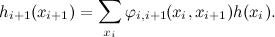
Общий случай
Общим случаем алгоритма передачи сообщений является случай, когда граф факторов дерево (т.е.в нем нет циклов).
В этом случае можно доказать, что для маргинализации относительно некоторой вершины достаточно:
- считайте эту вершину временным корнем дерева;
- передавать сообщения от листьев к корню; каждое сообщение является функцией ровно одной переменной — той, которая примыкает к ребру, по которому движется это сообщение;
- умножить все сообщения, поступающие в корень.
правило передачи сообщений: вершина факторного графа может передать сообщение своему соседу, если она уже получила сообщения от всех остальных соседей .
В частности, у листьев есть только один сосед, поэтому они сразу же начинают отправлять туда сообщения.
Вот так будут идти сообщения в типичном дереве (цифры указывают, в каком «цикле» будет генерироваться это сообщение; мы сейчас рассматриваем только сообщения, идущие снизу вверх).
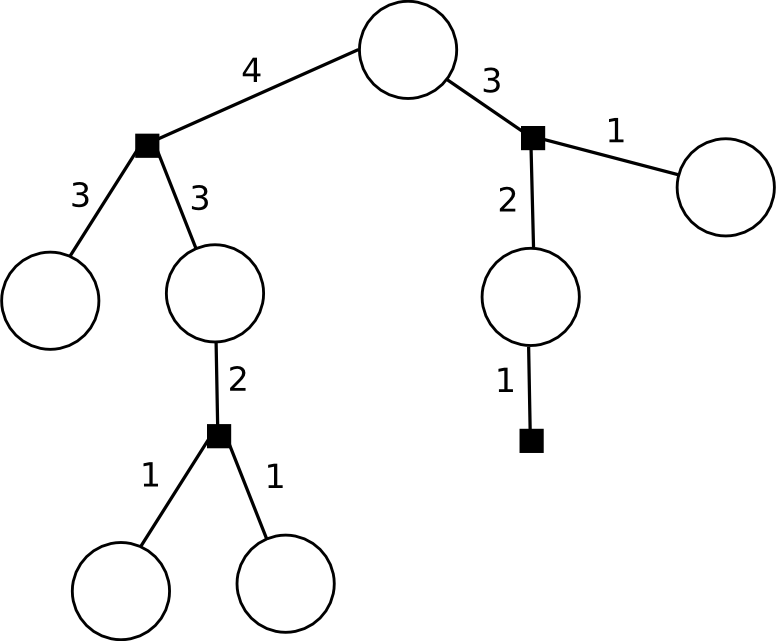
Сообщение, которое передает узел переменной, представляет собой просто произведение всех полученных им сообщений (в случае листа — идентичной единицы): 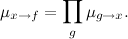
И чтобы пересчитать сообщение функционального узла, необходимо провести частичную маргинализацию; если функция 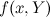
уже полученные сообщения 
из всех переменных 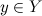
, он может передаваться в переменную Икс сообщение 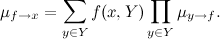
Листовая функция, соответственно, передает себя своему единственному соседу (произведение пусто).
Мы предполагаем здесь, что каждая функция, участвующая в разложении, зависит от достаточно малого числа переменных, чтобы эти суммирования можно было провести «грубой силой» (или хотя бы как-то, если возникнет особо сложный случай).
Завершение и анонс следующего эпизода
Алгоритм передачи сообщений работает только тогда, когда граф факторов представляет собой дерево.Если в графе фактора есть циклы, алгоритм не работает (представьте, что кроме цикла нет ничего — с чего же тогда начать?).
Однако в жизни часто встречаются ситуации, когда циклы все же присутствуют в графе факторов; например, модель LDA для тематического моделирования из последней серии вообще состоит из нескольких почти полных двудольных графов, каждый документ связан с каждой темой, в факторном графе имеются непрерывные циклы.
В следующий раз мы поговорим о том, что можно сделать в ситуации, когда в графе есть циклы.
Мы уже приближаемся к пределу того, что можно подробно объяснить, оставаясь при этом в здравом уме, в популярной статье, рассчитанной на широкую аудиторию, но в следующий раз я все же постараюсь дать немного интуиции.
А потом, пожалуй, перейдем к конкретным примерам.
Теги: #Байесовские сети #теория вероятностей #Интеллектуальный анализ данных #математическое моделирование #математика #Интеллектуальный анализ данных

-
Спутниковое Радио: Быстрое Расширение
19 Oct, 24 -
Подарить Ручку-Накопитель
19 Oct, 24 -
Серия Acer Extensa Ex5630 643G25Mn
19 Oct, 24 -
Компьютер На Луне
19 Oct, 24 -
Высокое Искусство 21 Века.
19 Oct, 24 -
Интервью В Геймдев-Индустрии
19 Oct, 24


