Бинарная куча — это простая в реализации структура данных, позволяющая быстро (за логарифмическое время) добавлять элементы и удалять элемент с максимальным приоритетом (например, максимальным значением).
Для дальнейшего чтения вам необходимо иметь представление о деревья , а также желательно знать о оценка сложности алгоритмов .
Алгоритмы в этой статье будут сопровождаться кодом на C#.
Введение
Бинарная куча — это полное двоичное дерево, для которого основное свойство кучи : приоритет каждой вершины больше приоритетов ее потомков.В простейшем случае приоритет каждой вершины можно считать равным ее значению.
В этом случае структура называется максимальная куча , поскольку корень поддерева — это максимальное из значений элементов поддерева.
В этой статье для простоты используется это представление.
Еще напомню, что дерево называется полный двоичный файл , если каждая вершина имеет не более двух потомков, а заполнение уровней вершин идет сверху вниз (в пределах одного уровня — слева направо).
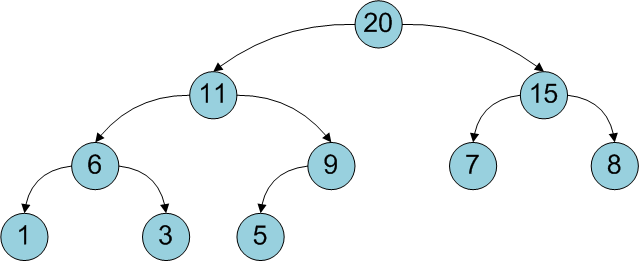
Бинарную кучу удобно хранить как одномерный массив с левым дочерним элементом вершины по индексу
имеет индексi
2*i+1, и правильный
2*i+2.
Корнем дерева является элемент с индексом 0. Высота двоичной кучи равна высоте дерева, то есть log 2 Н, где N
– количество элементов массива.
Вот пример класса на C#: public class BinaryHeap
{
private List<int> list;
public int heapSize
{
get
{
return this.list.Count();
}
}
}
Добавление элемента
Новый элемент добавляется на последнее место массива, то есть на позицию с индексом heapSize:
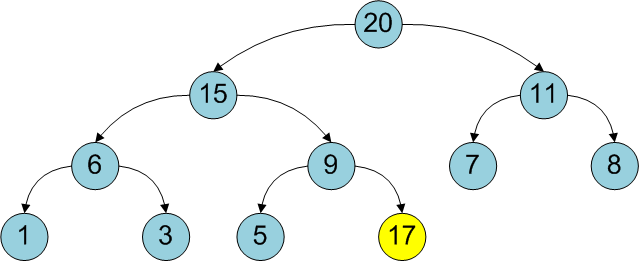
Возможно, это нарушит основное свойство кучи, поскольку новый элемент может быть больше своего родителя.
В этом случае следует «поднять» новый элемент на один уровень (изменить его родительским узлом) до тех пор, пока не будет выполнено базовое свойство кучи: 
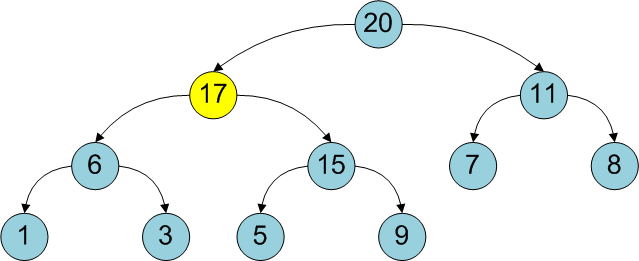
Другими словами, новый элемент «всплывает» и «подталкивается» вверх, пока не займет свое место.
Сложность алгоритма не превышает высоту двоичной кучи (поскольку количество «подъёмов» не превышает высоту дерева), то есть равна O(log 2 Н).
public void add(int value)
{
list.Add(value);
int i = heapSize - 1;
int parent = (i - 1) / 2;
while (i > 0 && list[parent] < list[i])
{
int temp = list[i];
list[i] = list[parent];
list[parent] = temp;
i = parent;
parent = (i - 1) / 2;
}
}
Упорядочение двоичной кучи
При других операциях с уже построенной бинарной кучей также может быть нарушено главное свойство кучи: вершина может стать меньше своего потомка.

Метод heapify
восстанавливает базовое свойство кучи для дерева с корнем в i-й вершине при условии, что оба поддерева удовлетворяют этому свойству.
Для этого необходимо «опустить» i-ю вершину (поменять местами с наибольшим из потомков) до тех пор, пока основное свойство не будет восстановлено (процесс завершается, когда не останется потомка большего, чем его родитель).
Легко понять, что сложность этого алгоритма также равна O(log 2 Н).


public void heapify(int i)
{
int leftChild;
int rightChild;
int largestChild;
for (; ; )
{
leftChild = 2 * i + 1;
rightChild = 2 * i + 2;
largestChild = i;
if (leftChild < heapSize && list[leftChild] > list[largestChild])
{
largestChild = leftChild;
}
if (rightChild < heapSize && list[rightChild] > list[largestChild])
{
largestChild = rightChild;
}
if (largestChild == i)
{
break;
}
int temp = list[i];
list[i] = list[largestChild];
list[largestChild] = temp;
i = largestChild;
}
}
Создание двоичной кучи
Самый очевидный способ построить кучу из неупорядоченного массива — добавить все его элементы по одному.Оценка времени для такого алгоритма составляет O(N log 2 Н).
Однако построить кучу можно еще быстрее — за O(N).
Сначала следует построить дерево из всех элементов массива, не заботясь о соблюдении базового свойства кучи, а затем вызвать метод heapify
для всех вершин, имеющих хотя бы одного дочернего элемента (поскольку поддеревья, состоящие из одной вершины и не имеющие дочерних элементов, уже упорядочены).
У первых гарантированно будут потомки heapSize/2
пики public void buildHeap(int[] sourceArray)
{
list = sourceArray.ToList();
for (int i = heapSize / 2; i >= 0; i--)
{
heapify(i);
}
}
Получение (удаление) максимального элемента
В упорядоченном виде max-heapмаксимальный элемент всегда хранится в корне.
Вы можете восстановить порядок двоичной кучи после удаления максимального элемента, заменив его последним элементом и вызвав heapify
для корня, то есть упорядочивания всего дерева.
public int getMax()
{
int result = list[0];
list[0] = list[heapSize - 1];
list.RemoveAt(heapSize - 1);
return result;
}
Двоичная сортировка кучи
Обратите внимание, что вы можете отсортировать массив, сначала построив из него двоичную кучу, а затем последовательно извлекая максимальное количество элементов.
Оценим временную сложность такого элемента: построение кучи - O(N), поиск N
элементы – O(N log 2 Н).
Следовательно, окончательная оценка равна O(N log 2 Н).
При этом дополнительная память для массива не используется.
public void heapSort(int[] array)
{
buildHeap(array);
for (int i = array.Length - 1; i >= 0; i--)
{
array[i] = getMax();
heapify(0);
}
}
Заключение
Таким образом, двоичная куча имеет древовидную структуру логарифмической высоты (относительно количества вершин), позволяет добавлять элементы за логарифмическое время и удалять элемент с максимальным приоритетом за постоянное время.При этом двоичная куча проста в реализации и не требует дополнительной памяти.
Теги: #двоичная куча #бинарные деревья #структуры данных #двоичная куча #Алгоритмы

-
Поддержите Нашу Команду Imagine Cup
19 Oct, 24 -
Кредиты Втб24 И Отношение К Клиентам
19 Oct, 24 -
Рельсы Эшафот Новости — Как?
19 Oct, 24


