Автор: Иннокентий Сенновский ( румата888 ) Хочу поделиться своим опытом регистрации уязвимостей в продуктах компаний без Bug Bounty. Этот процесс занял у меня целых два года, в течение которых я общался с вендорами, боролся с недоразумениями и стучался в двери MITRE. Проблемы мотивации и целесообразности поиска уязвимостей в подобных продуктах мы оставим за рамками данной статьи.
Давайте обсудим, что делать, если ошибка уже обнаружена.
Если вам не терпится сразу же прочитать советы, перейдите к последней части.

Фото предоставлено: https://www.deviantart.com/heroeswho
Незапланированная охота за ошибками, или Как все начиналось
В 2018 году мы с командой придумали плату с двумя чипами для задачи CTF: один с базовой логикой, другой для аутентификации.Предполагалось, что в случае успешной эксплуатации встроенных уязвимостей злоумышленники смогут загрузить свой вредоносный код в память логического чипа, но не смогут взломать чип аутентификации.
У атакующей команды не было возможности клонировать устройство и впоследствии эмулировать его.
Чтобы получить флаг в каждом раунде, ей приходилось взаимодействовать с чипом аутентификации на целевом устройстве.
Обычно такие механизмы требуют криптографических решений.
Поскольку мы планировали использовать чипы STM для обоих микроконтроллеров, я обрадовался (как оказалось, преждевременно), когда узнал, что ST предоставляет для своих устройств предварительно скомпилированные криптографические библиотеки под названием Расширение программного обеспечения библиотеки криптографических прошивок STM32 для STM32Cube (X-CUBE-CRYPTOLIB) .
Я решил их изучить и наткнулся в разделе RSA на одну вещь, которая меня насторожила: в библиотеке прошивки было 4 экспортируемые функции, представленные в таблице ниже.
| Имя функции | Описание |
|---|---|
| RSA_PKCS1v15_Sign | PKCS#1v1.5 Функция генерации подписи RSA — функция генерации подписи |
| RSA_PKCS1v15_Verify | PKCS#1v1.5 Функция проверки подписи RSA — функция проверки подписи |
| RSA_PKCS1v15_Encrypt | PKCS#1v1.5 Функция шифрования RSA — функция шифрования |
| RSA_PKCS1v15_Decrypt | PKCS#1v1.5 RSA Decryption Function — функция дешифрования |
Вот почему вы не можете использовать PKCS#1v1.5.
ПККС#1v1.5
PKCS#1 — это криптографический стандарт (спецификация) для алгоритма RSA. Он определяет примитивы и схемы использования RSA для шифрования и подписи с открытым ключом.Текущая версия стандарта — 2.2, но библиотека X-CUBE-CRYPTOLIB использует версию 1.5. Он раскрывает критическую уязвимость, возникающую в процессе шифрования и дешифрования.
Базовое адаптивное поисковое объявление
Примитив RSA основан на вычислительной сложности задачи факторизации произведения двух больших простых чисел.Давайте представим, что Боб собирается отправить Алисе сообщение, которое сможет прочитать только она.
Они выбирают следующий алгоритм:
- Алиса случайным образом выбирает два простых числа ( п И д ) заданной длины (например, 1024 кусочек).
- Алиса вычисляет результат их умножения – Н (модуль).
- Алиса принимает заданное значение публичного показателя степени.
е .
Обычно это 65537 , поскольку в двоичном представлении этого числа только два бита ненулевые.
Ранее также использовался 3 И 17 , но при возведении в степень превышение модуля не гарантировалось.
- Алиса вычисляет частный показатель д .
Теперь у нее закрытый( д , Н ) и открытые ключи ( е , Н ).
- Алиса отправляет свой открытый ключ Бобу.
- Боб преобразует сообщение М , который он собирается отправить Алисе, в количестве м , что меньше Н .
Он возводит число в степень е по модулю Н и отправляет сообщение Алисе.
- Алиса принимает результат и возводит его в степень д по модулю Н и, наконец, получает исходный номер м , который преобразуется обратно в М .
, Где п , д - простые числа
, Где
Проблемные области RSA
Для вычисления модуля нельзя просто выбрать два любых простых числа — они должны соответствовать определённым требованиям, иначе примитив становится небезопасным.Но даже если выбраны идеальные п И д , остаются другие проблемы.
Далее по тексту м - открытый текст (сообщение) и с - закрытый текст. Вот что произойдет, если вместо этого 65537 для открытого значения степени выберите меньшее значение, например, 3 .
Если п И д равны 1024 битам, то модуль будет состоять из 2048 бит или 256 байт. Если сообщения, которые Боб собирается отправить Алисе, меньше или равны
, то результат возведения в степень не превысит значения модуля.
В этом случае расшифровка текста не составит труда: достаточно извлечь третий корень.
Если Боб неоднократно отправляет сообщения, они шифруются одинаково, поэтому при реализации MitM-атаки злоумышленник может частично извлечь информацию о них: в определенные моменты времени Боб отправляет одни и те же сообщения.
Спецификация PKCS#1v1.5
Чтобы решить эти проблемы, RSA разработала спецификацию PKCS#1 v1.5 (стандарты криптографии с открытым ключом).Он обеспечивает форматирование зашифрованных и подписанных блоков с помощью специального дополнения — заполнения.
Заполнение применяется до того, как блок будет полностью зашифрован.
Предположим, что длина модуля Н в октетах (байтах) равно к .
Данные шифрования/подписи – Д .
В результате получается следующий блок: ЭБ = 00 || БТ || PS || 00 || Д, Где БТ равно 00 или 01 для операций с закрытым ключом (подписей) и 02 для операций с шифрованием с открытым ключом.
Блок преобразуется в целое число с использованием преобразования с прямым порядком байтов (первый октет ?.
Б.
наиболее значимый).
ПС состоит из октетов к-3-лен(Д) .
Его содержание зависит от БТ :
- Если БТ равно 00 , все октеты в ПС стать равным 00 ;
- Если БТ равно 01 , все октеты в ПС стать равным ФФ ;
- Если БТ равно 02 , все октеты в ПС генерируются псевдослучайно и не равны 00 .
- в БТ , равный 01 , вы можете удалить дополнение из Д независимо от его содержания;
- в БТ , равный 00 , из первого байта данных Д , равный 00 , дополнение также будет удалено, что создаст проблему;
- БТ , равный 01 , И БТ , равный 02 , генерируют большие целые числа для шифрования, поэтому все атаки, требующие небольшого значения открытого текста, терпят неудачу.
Б.
равно 00 .
Это значение было выбрано таким образом, чтобы полученное целое число ?.
Б.
, модуля всегда было меньше Н .
На первый взгляд данная схема кажется вполне надежной и решает перечисленные выше проблемы.
Но если бы все было так здорово, я бы не писал эту статью.
Атака оракула Бляйхенбахера
Речь идет о нападении уже 22 года.Чтобы понять это, давайте вернемся к Алисе и представим, что она уже создала пару ключей и отправила открытый ключ Бобу, но теперь оба используют заполнение из PKCS#1v1.5 в своих зашифрованных сообщениях.
Вот что происходит, когда зашифрованный текст отправляется Алисе:
- Алиса расшифровывает текст, используя примитив RSA;
- Алиса удаляет дополнение из сообщения;
- Алиса анализирует сообщение и предпринимает действия в зависимости от его содержания.
Такие сигналы часто показывают, где именно возникла проблема: на втором этапе (неверное сложение) или на третьем (что-то не так с самой командой).
Распознавание второго и третьего этапов, как правило, возможно только с помощью закрытого ключа.
Следовательно, когда Алиса сообщает, что заполнение было успешным или неудачным, она фактически раскрывает информацию об открытом тексте.
В качестве мысленного эксперимента давайте посмотрим, что произойдет, если мы отправим для расшифровки произвольное целое число вместо обычного сообщения.
Какова вероятность того, что при удалении дополнения не возникнет ошибка? Первые два октета ?.
Б.
должно быть представлено как 00 || 02 , остальные октеты имеют хотя бы одно значение 00 .
Если к равно 256, тогда
Вероятность кажется слишком низкой, но на самом деле она достаточно высока, чтобы злоумышленник мог ею воспользоваться.
Атака использует гомоморфизм RSA по отношению к умножению:
Вот как развивается атака.
Мы выбираем с , для которого мы хотим найти
Для удобства в дальнейшем объяснении мы будем использовать следующие константы:
Если полученный открытый текст соответствует спецификации PKCS, то и зашифрованный текст также соответствует. Мы выбираем целые числа с , рассчитать
и отправьте их к оракулу (Алисе).
Если
проходит проверку ошибок, затем
Получив необходимое количество разных значений с , мы можем найти м .
Обычно это занимает около 2 20 зашифрованные тексты, но их количество сильно варьируется.
Существует три стадии атаки:
- Ослепление зашифрованного текста, создание
, что соответствует неизвестной величине
. - Вычисление небольшого значения
, к
соответствует требованиям PKCS. Для всех таких
злоумышленник, используя известную информацию, вычисляет интервалы, которые должны содержать
. - Постепенное увеличение стоимости
, сужая возможный диапазон
пока не останется только одно возможное значение.Этот этап начинается, когда остается только один интервал.
Злоумышленник располагает достаточной информацией о
чтобы выбрать это
, при котором вероятность совпадения
Спецификация PKCS выше, чем у случайно выбранного сообщения.Если интервал достаточно мал, эффективнее угадывать значения локально, чем продолжать отправлять запросы оракулу.
- перехват сообщения Боба Алисе;
- использование Алисы в качестве оракула для расшифровки сообщения.
Оказывается, Microchip также предоставляет библиотеку криптографических примитивов и, кто бы мог подумать, единственная схема шифрования для RSA — это PKCS#1v1.5. Вот фрагмент функции дешифрования RSA:
Байты памяти расположены в обратном порядке, поэтому мы видим, что открытый текст заканчивается на 0200 вместо проверки доступности 0002 сначала.// Find the message length endPtr = (uint8_t *)tmpPtr->startAddress + rsaDesc0.cT.bLength - 1; if ((*endPtr-- == 0x00) && (*endPtr-- == 0x02)) { while ((endPtr >= (uint8_t *)tmpPtr->startAddress) && (*endPtr-- != 0x00)); if ((endPtr - (uint8_t *)tmpPtr->startAddress + 1) > rsaDesc0.cT.bLength - 11) { rsaDesc0.status = RSA_SW_STATUS_ERROR; } else { *msgLen = endPtr - (uint8_t *)tmpPtr->startAddress + 1; if (endPtr >= (uint8_t *)tmpPtr->startAddress) { uint8_t i = 0; while (endPtr >= (uint8_t *)tmpPtr->startAddress) { *(plainText + i++) = *endPtr--; } } } } else { rsaDesc0.status = RSA_SW_STATUS_ERROR; }
Если дополнение неверно, функция возвращает другой статус, что делает ее опасной.
Время постучать в дверь производителя
В сентябре 2018 года я отправил описание уязвимостей в ST и Microchip, и вот к чему это привело.Представители СТ изначально активно отвечали на мои письма, но в процессе общения у нас возникло недопонимание.
Частично это была моя вина: я указал, что ошибка была в STM32-CRYP-LIB (это еще одна криптографическая библиотека ST) вместо X-CUBE-CRYPTOLIB. Дело в том, что STM32-CRYP-LIB не содержит примитивов шифрования и дешифрования для RSA, а только примитивы подписи или проверки.
Мое обоснование угрозы атаки Блейхенбахера Padding Oracle из-за ошибки было встречено сопротивлением, поскольку это не обязательно означает, что конечный продукт уязвим.
Однако команда ST согласилась, что проблему сложно решить при использовании PKCS#1v1.5. В октябре 2018 года мне сообщили, что началась разработка PKCS#1v2.2. Я подчеркнул, что уведомлять пользователей об уязвимостях по-прежнему необходимо.
В декабре 2018 года я получил ответ, основное содержание которого сводится к двум пунктам:
- ST не захотела регистрировать уязвимость в базе данных CVE, так как производители следовали спецификации, а сама библиотека не выдавала ошибок дополнений (это верно лишь отчасти);
- началась разработка PKCS#1v2.2, новой версии спецификации с более безопасным дополнением, выпуск которой был запланирован на весну вместе с обновленной библиотекой X-CUBE-CRYPTOLIB.
Я отправил отчет в Microchip в сентябре 2018 года.
Команда разработчиков ответила только в марте 2019 года, предложив решение проблемы: вместо пакета MLA они посоветовали использовать Microchip Harmony — фреймворк для разработки ПО для встраиваемых устройств.
Это действительно должно сработать, поскольку Harmony содержит более современные спецификации, которые можно использовать вместо уязвимой.
Однако пользователей по-прежнему необходимо информировать об опасностях использования RSA в MLA. Но так как Microchip ответил на мой первый запрос полгода, я решил больше не ждать, а искать другие пути.
Еще пара попыток получить CVE
Связаться с MITRE напрямую можно только после того, как другие попытки не увенчались успехом, поэтому я решил попробовать присоединиться.Интернет - Программа HackerOne. Для этого нужно найти уязвимость в популярном проекте с открытым исходным кодом или уязвимость, которая затронет многих вендоров, что как раз и является моим случаем.
Остается только предоставить подтверждение концепции (PoC).
Вот несколько технических особенностей, которые я выявил, когда начал работать над PoC. Учитывая, что эти библиотеки предназначены для встраиваемых устройств, их использование на стандартных компьютерах с архитектурой AMD64 имеет некоторые ограничения.
Библиотека MLA распространяется в виде исходного кода, но как таковые вычисления bigint реализованы в ассемблере архитектуры PIC. Пришлось их переписать на архитектуру AMD64. Это заняло много времени, поскольку ключевые вычисления были рассчитаны на 16-битную архитектуру.
Это сильно замедляет RSA, несмотря на его встроенное исполнение.
Атака может занять несколько дней.
Гораздо быстрее на встроенном устройстве.
X-CUBE-CRYPTOLIB распространяется в скомпилированном формате.
Чтобы использовать его на обычном компьютере, мне пришлось эмулировать прошивку с помощью QEMU, что крайне негативно сказывается на производительности.
Вдобавок ко всему, единственный подходящий интерфейс для передачи данных — это мучительно медленный эмулируемый UART (передача 256 байт занимает 2 минуты).
Чтобы решить проблему с интерфейсом, я установил отладочный крючок, который передает данные в память и из нее.
По крайней мере, так вы сможете избежать проблем, связанных с эмуляцией передачи.
Однако даже в таких условиях реализация атаки идет очень медленно.
Поэтому, чтобы сэкономить время тестировщика, я написал по две версии атаки для каждой платформы:
- полный цикл атаки (на библиотеке MLA это займет много времени, на ST — нереально много времени);
- атака с заранее рассчитанными успешными шагами.
В нем хранятся все шаги, которые обеспечивают успешное зачистку и позволяют сузить область открытого текста.
Соответственно, злоумышленник применяет только эти шаги к уязвимой реализации, избегая болезненного перебора.
Также следует отметить, что библиотека X-CUBE-CRYPTOLIB защищена от использования на устройствах, отличных от ST (проверка осуществляется путем записи и чтения битов из специальных регистров памяти).
Они представлены на рисунке ниже (доступы к ПАМЯТИ).
К счастью, QEMU не проходит проверку: вместо того, чтобы отказываться расшифровывать или шифровать данные, процессы просто маскируют данные во время шифрования и возвращают больше данных (включая некоторые произвольные дополнения).
Маскирование можно откатить, если простой текст содержит только символы ASCII-7, так как все они меньше 128. Поэтому для использования библиотеки с помощью QEMU нам пришлось реализовать функцию демаскирования.
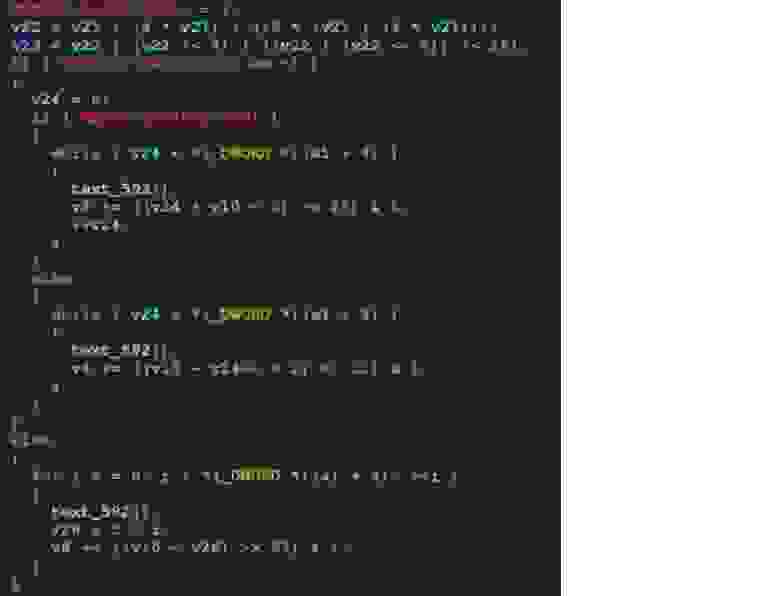
Единственным изменением, внесенным в библиотеку MLA, стала реализация bigint для арифметических операций в ассемблере Intel вместо PIC. В библиотеку ST не было внесено никаких изменений.
Если вас интересует полная версия PoC, зайти на Гитхаб .
Итак, в октябре 2019 года я подготовил и отправил PoC в HackerOne. Но и здесь ничего не работало: найденные мной ошибки не прошли уровень критичности.
Увы.
К этому моменту я перепробовал все и мог с чистой совестью связаться с MITRE. 21 октября я написал им и получил пустой ответ. Несколько дней спустя я спросил, нужна ли дополнительная информация, но никто не ответил.
В результате я погрузился в работу и совершенно забыл об этом письме.
Счастливый конец
В декабре 2019 представители ST вернулись ко мне с новостью: в начале 2020 года они планируют опубликовать новую версию библиотеки со спецификацией PKCS#1v2.2, а также обновление руководства пользователя X-CUBE-CRYPTOLIB, которое будет включать предупреждение об уязвимости.Библиотека не обновилась по сей день, но появилось предупреждение (см.
Рис.
1).

Рис.
1. Скриншот из документации Позже, в октябре 2020 года, мне напомнили об этих уязвимостях.
Я отправил еще один запрос в MITRE, но не получил ответа.
Я решил не сдаваться, через две недели попробовал еще раз и.
Опять тишина.
Потом я понял, что с момента первого письма в MITRE прошел уже год. В такой ситуации есть только одно эффективное решение – возмущение в Твиттере.
Рис.
2. Тот самый твит Это сработало! Сразу после упоминания в твите MITRE зарезервировал номера в базе данных CVE и ответил на все мои старые письма.
Об уязвимостях сообщили:
- CVE-2020-20949 — уязвимость в библиотеке ST: X-CUBE-CRYPTOLIB 3.1.0, 3.1.2);
- CVE-2020-20950 — уязвимость в библиотеке Microchip Libraries for Applications 26 ноября 2018 г.
).
5 шагов к регистрации уязвимости в продуктах компании без Bug Bounty
Вот что я бы посоветовал тем, кто нашел уязвимость в продукте компании без программы Bug Bounty и security.txt:- Оцените, стоят ли регистрация и исправление ошибки усилий, которые вы потратите на PoC. Короче, оно вам действительно нужно?))
- Если баг вас не дает и вы решили, что он вам еще нужен, напишите продавцу.
Обязательно укажите сроки, в течение которых вы ожидаете ответа и устранения уязвимости.
Рекомендую дать две недели на ответ на первое письмо.
Стандартный срок исправления ошибки — 90 дней.
Имейте в виду, что иногда компании по объективным причинам требуется больше времени, чем вам требуется.
В этом случае лучше уступить и договориться об отсрочке.
- Если компания вас игнорирует или не считает проблему уязвимостью, определите, сколько времени вы готовы потратить на ее решение.
бороться за справедливостьработа с сопротивлением.Когда он истечет, бегите в MITRE.
- Если MITRE игнорирует вас две недели (получил только отпор, номера CVE до сих пор не выделены), то напишите в Твиттер с тегом @CVENew.
- Как только номера CVE будут выделены, напишите статью и отправьте ее в MITRE и поставщику.

-
Хабр Сломан
19 Oct, 24 -
Необычные Животные В Доме
19 Oct, 24 -
Как Наша Нейросеть Общалась С Фсб
19 Oct, 24 -
Субстики №127
19 Oct, 24 -
Кохана 3.0 – Упрощаем Вашу Жизнь
19 Oct, 24 -
Directaccess В Windows 7. Часть 3
19 Oct, 24


