
На днях завершился очередной чемпионат мира по хоккею.
Во время просмотра матчей родилась идея.
Когда телекамера показывает, как игроки в перерывах уходят в раздевалку, трудно не заметить, насколько они огромные.
На фоне тренеров, официальных лиц команд, сотрудников ледовой арены, журналистов или просто болельщиков они обычно выглядят очень эффектно.
Вот, например, восходящие звезды финского хоккея Патрик Лайне и Александр Барков вместе со своими преданными болельщиками.

Источник И я задавал себе вопросы.
Действительно ли хоккеисты выше обычных людей? Как со временем меняется рост хоккеистов по сравнению с обычными людьми? Существуют ли постоянные различия между странами?
Данные
ИИХФ, организация, которая проводит чемпионаты мира по хоккею, ежегодно публикует составы участвующих команд с информацией о росте и весе каждого игрока.Архив этих данных здесь .
Я собрал данные со всех чемпионатов мира с 2001 по 2016 год. Формат предоставления данных немного меняется от года к году, что требует определённых усилий по его очистке.
Не имея представления, как правильно автоматизировать процесс, я скопировал все данные вручную, что заняло чуть больше 3 часов.
Объединенный набор данных опубликовано публично .
код Р.
Подготовка к работе, загрузка данных
# load required packages require(dplyr) # data manipulation require(lubridate) # easy manipulations with dates require(ggplot2) # visualization require(ggthemes) # themes for ggplot2 require(cowplot) # nice alignment of the ggplots require(RColorBrewer) # generate color palettes require(texreg) # easy export of regression tables require(xtable) # export a data frame into an html table # download the IIHF data set; if there are some problems, you can download manually # using the stable URL ( https://dx.doi.org/10.6084/m9.figshare.3394735.v2 ) df <- read.csv(' https://ndownloader.figshare.com/files/5303173 ') # color palette brbg11 <- brewer.pal(11,'BrBG')
Растут ли хоккеисты? Грубое (периодическое) сравнение
Для начала сравним средний рост игроков на всех 16 чемпионатах мира.
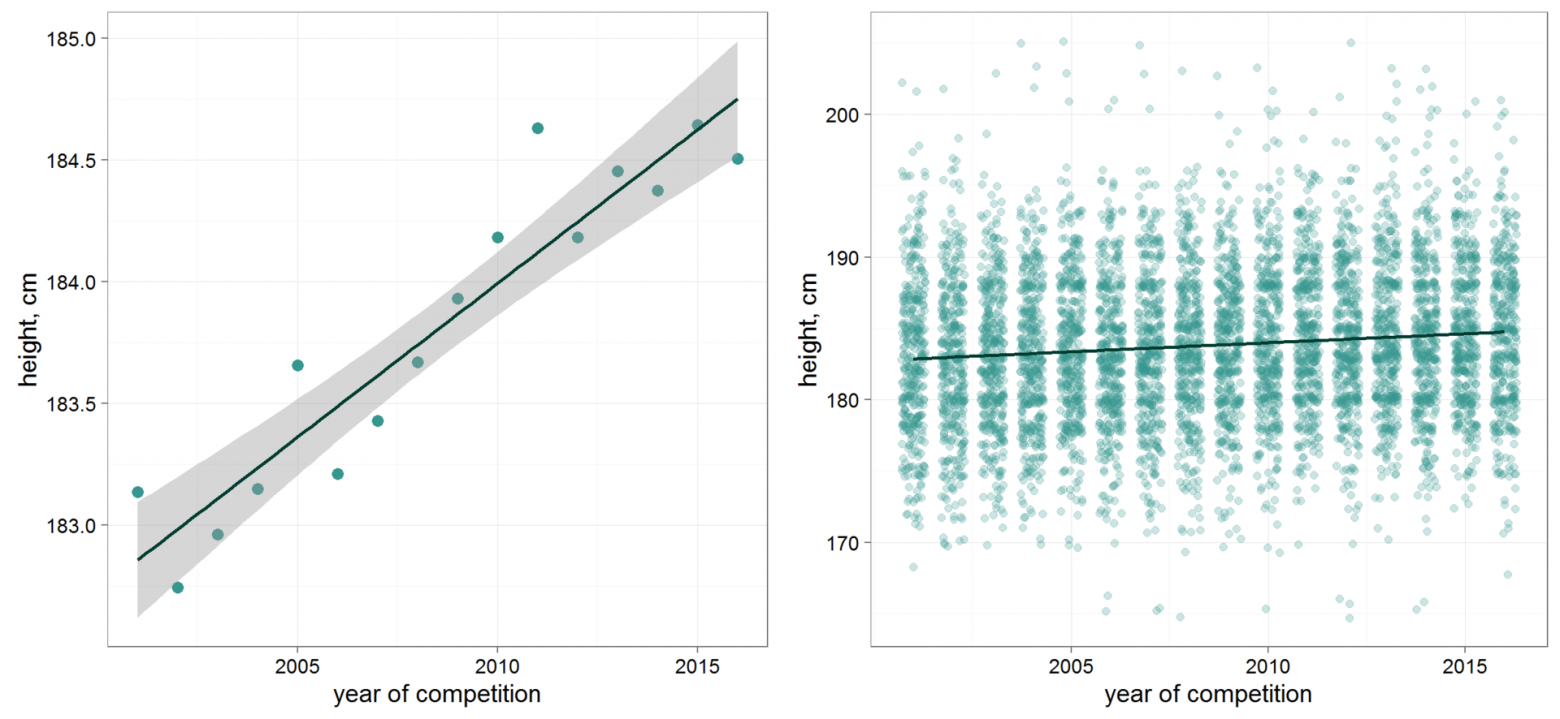
код Р.
Рисунок 1. Изменение среднего роста хоккеистов на чемпионатах мира, 2001-2016 гг.
# mean height by championship
df_per <- df %>% group_by(year) %>%
summarise(height=mean(height))
gg_period_mean <- ggplot(df_per, aes(x=year,y=height))+
geom_point(size=3,color=brbg11[9])+
stat_smooth(method='lm',size=1,color=brbg11[11])+
ylab('height, cm')+
xlab('year of competition')+
scale_x_continuous(breaks=seq(2005,2015,5),labels=seq(2005,2015,5))+
theme_few(base_size = 15)+
theme(panel.grid=element_line(colour = 'grey75',size=.
25)) gg_period_jitter <- ggplot(df, aes(x=year,y=height))+ geom_jitter(size=2,color=brbg11[9],alpha=.
25,width = .
75)+ stat_smooth(method='lm',size=1,se=F,color=brbg11[11])+ ylab('height, cm')+ xlab('year of competition')+ scale_x_continuous(breaks=seq(2005,2015,5),labels=seq(2005,2015,5))+ theme_few(base_size = 15)+ theme(panel.grid=element_line(colour = 'grey75',size=.
25))
gg_period <- plot_grid(gg_period_mean,gg_period_jitter)
Позитивная тенденция очевидна.
За полтора десятилетия средний рост хоккеиста на чемпионате мира увеличился почти на 2 сантиметра (левая панель).
Это кажется незначительным увеличением на фоне довольно большого разброса (правая панель).
Это много или мало? Чтобы ответить на вопрос, нам нужно правильно сравнить ее с численностью населения (но об этом ближе к концу статьи).
Когортный анализ
Более точный способ изучения изменений роста предполагает сравнение возрастных когорт. Здесь мы сталкиваемся с интересным нюансом – некоторые хоккеисты участвовали не в одном чемпионате мира.Вопрос: Должен ли я удалить повторяющиеся записи для одних и тех же людей? Если нас интересует средний рост хоккеиста на чемпионате (как на картинке выше), то, наверное, не имеет смысла прояснять.
Но если мы хотим отслеживать изменения роста хоккеистов как таковые, то, на мой взгляд, было бы неправильно придавать больший вес тем игрокам, которые более регулярно выезжали на чемпионаты мира.
Поэтому для дальнейшего анализа я очистил данные от повторных записей одних и тех же игроков.
код Р.
Подготовка данных для когортного анализа # remove double counts
dfu_h <- df %>% select(year,name,country,position,birth,cohort,height) %>%
spread(year,height)
dfu_h$av.height <- apply(dfu_h[,6:21],1,mean,na.rm=T)
dfu_h$times_participated <- apply(!is.na(dfu_h[,6:21]),1,sum)
dfu_w <- df %>% select(year,name,country,position,birth,cohort,weight) %>%
spread(year,weight)
dfu_w$av.weight <- apply(dfu_w[,6:21],1,mean,na.rm=T)
dfu <- left_join(dfu_h %>% select(name,country,position,birth,cohort,av.height,times_participated),
dfu_w %>% select(name,country,position,birth,cohort,av.weight),
by = c('name','country','position','birth','cohort')) %>%
mutate(bmi = av.weight/(av.height/100)^2)
Общее количество наблюдений сокращалось с 6292 до 3333. Если хоккеист участвовал более чем в одном чемпионате мира, я усреднял данные роста и веса, так как рост и (особенно) вес отдельного хоккеиста могли меняться с течением времени.
Сколько раз хоккеисты удостаивались чести выступать за сборные на чемпионатах мира? В среднем чуть меньше, чем в 2 раза.

код Р.
Рисунок 2. Гистограмма распределения хоккеистов по количеству участия в чемпионате мира.
# frequencies of participation in world championships
mean(dfu$times_participated)
df_part <- as.data.frame(table(dfu$times_participated))
gg_times_part <- ggplot(df_part,aes(y=Freq,x=Var1))+
geom_bar(stat='identity',fill=brbg11[9])+
ylab('# of players')+
xlab('times participated (out of 16 possible)')+
theme_few(base_size = 15)
Но есть и уникальные.
Давайте посмотрим, какие игроки принимали участие хотя бы в 10 чемпионатах мира.
Таких игроков было 14. код Р.
Таблица 1. Лидеры участия в чемпионатах мира # the leaders of participation in world championships
# save the table to html
leaders <- dfu %>% filter(times_participated > 9)
View(leaders)
print(xtable(leaders), type="html", file="table_leaders.html")
| имя | страна | позиция | рождение | когорта | средняя высота | times_participated | средний вес | ИМТ | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Овечкин Александр | РУСЬ | Ф | 1985-09-17 | 1985 | 188.45 | 11 | 98.36 | 27.70 |
| 2 | Нильсен Дэниел | ДЕН | Д | 1980-10-31 | 1980 | 182.27 | 11 | 79.73 | 24.00 |
| 3 | Стаал Ким | ДЕН | Ф | 1978-03-10 | 1978 | 182.00 | 10 | 87.80 | 26.51 |
| 4 | зеленый мортен | ДЕН | Ф | 1981-03-19 | 1981 | 183.00 | 12 | 85.83 | 25.63 |
| 5 | Масальскис Эдгарс | Латвия | г | 1980-03-31 | 1980 | 176.00 | 12 | 79.17 | 25.56 |
| 6 | Амбюль Андрес | СУИ | Ф | 1983-09-14 | 1983 | 176.80 | 10 | 83.70 | 26.78 |
| 7 | Гранак Доминик | СВК | Д | 1983-06-11 | 1983 | 182.00 | 10 | 79.50 | 24.00 |
| 8 | Мэдсен Мортен | ДЕН | Ф | 1987-01-16 | 1987 | 189.82 | 11 | 86.00 | 23.87 |
| 9 | Редлихс Микелис | Латвия | Ф | 1984-07-01 | 1984 | 180.00 | 10 | 80.40 | 24.81 |
| 10 | Ципулис Мартинс | Латвия | Ф | 1980-11-29 | 1980 | 180.70 | 10 | 82.10 | 25.14 |
| 11 | голос Джонас | НИ | Д | 1987-08-27 | 1987 | 180.18 | 11 | 91.36 | 28.14 |
| 12 | Бастиансен Андерс | НИ | Ф | 1980-10-31 | 1980 | 190.00 | 11 | 93.64 | 25.94 |
| 13 | спросить Мортена | НИ | Ф | 1980-05-14 | 1980 | 185.00 | 10 | 88.30 | 25.80 |
| 14 | Форсберг Кристиан | НИ | Ф | 1986-05-05 | 1986 | 184.50 | 10 | 87.50 | 25.70 |
рисунок 3) и стабильно ли игрок входил в состав национальной сборной; Наконец, есть еще НХЛ, которая постоянно отвлекает лучших из лучших от участия в чемпионатах мира.
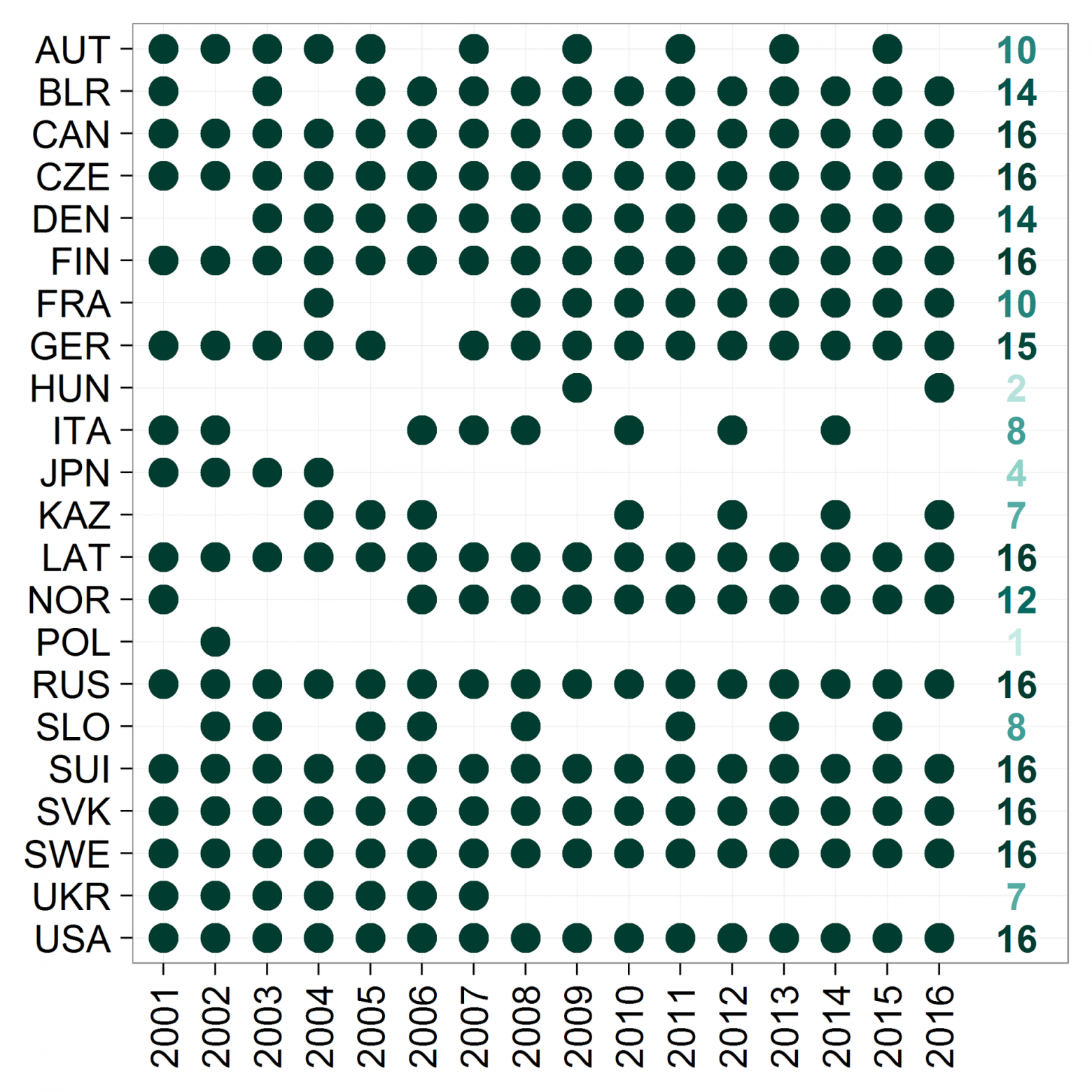
код Р.
Рисунок 3. Участие национальных сборных в чемпионатах мира по хоккею в 2001-2016 гг.
# countries times participated
df_cnt_part <- df %>% select(year,country,no) %>%
mutate(country=factor(paste(country))) %>%
group_by(country,year) %>%
summarise(value=sum(as.numeric(no))) %>%
mutate(value=1) %>%
ungroup() %>%
mutate(country=factor(country, levels = rev(levels(country))),
year=factor(year))
d_cnt_n <- df_cnt_part %>% group_by(country) %>%
summarise(n=sum(value))
gg_cnt_part <- ggplot(data = df_cnt_part, aes(x=year,y=country))+
geom_point(color=brbg11[11],size=7)+
geom_text(data=d_cnt_n,aes(y=country,x=17.5,label=n,color=n),size=7,fontface=2)+
geom_text(data=d_cnt_n,aes(y=country,x=18.5,label=' '),size=7)+
scale_color_gradientn(colours = brbg11[7:11])+
xlab(NULL)+
ylab(NULL)+
theme_bw(base_size = 25)+
theme(legend.position='none',
axis.text.x = element_text(angle = 90, hjust = 1,vjust=0.5))
Растут ли хоккеисты? Регрессивный анализ
Регрессионный анализ позволяет более правильно ответить на вопрос об изменении роста игроков.В этом случае используется полиномиальная линейная регрессия для прогнозирования роста хоккеиста в зависимости от когорты рождения.
Включая в спецификацию регрессионной модели различные дополнительные (контрольные) переменные, мы получаем значение наиболее интересующего нас коэффициента «при прочих равных условиях».
Например, добавляя положение игрока к объясняющим переменным, отличным от когорты по рождению, мы получаем соотношение роста и когорты, свободное от влияния различий по положению; Добавляя страны к контрольным переменным, мы получаем результат, очищенный от межстрановых различий.
Конечно, если сами переменные управления окажутся значимыми, на это тоже стоит обратить внимание.
Модели регрессии (особенно линейные регрессии) очень чувствительны к выбросам (см.
, например, Эта статья ).
Не вдаваясь глубоко в эту обширную тему, я исключил из анализа лишь те когорты, представителей которых у нас слишком мало.
код Р.
Удаление небольших когорт # remove small cohorts
table(dfu$cohort)
dfuc <- dfu %>% filter(cohort<1997,cohort>1963)
Не желая слишком сильно сокращать данные, я удалил только когорты 1963, 1997 и 1998 годов рождения, в которых у нас менее 10 игроков.
Итак, результаты регрессионного анализа.
В каждую последующую модель я добавляю по одной переменной.
Зависимая переменная : рост хоккеиста.
Независимые переменные : 1) когорта рождения; 2) + позиция на поле (сравнение с защитниками); 3) + страна (сравнение с Россией).
код Р.
Таблица 2. Результаты регрессионного анализа # relevel counrty variable to compare with Russia
dfuc$country <- relevel(dfuc$country,ref = 'RUS')
# regression models
m1 <- lm(data = dfuc,av.height~cohort)
m2 <- lm(data = dfuc,av.height~cohort+position)
m3 <- lm(data = dfuc,av.height~cohort+position+country)
# export the models to html
htmlreg(list(m1,m2,m3),file = 'models_height.html',single.row = T)
| Модель 1 | Модель 2 | Модель 3 | |
|---|---|---|---|
| (Перехват) | -10.17 (27.67) | -18.64 (27.01) | 32.59 (27.00) |
| когорта | 0.10 (0.01) *** | 0.10 (0.01) *** | 0.08 (0.01) *** |
| позицияF | -2.59 (0.20) *** | -2.59 (0.20) *** | |
| позицияG | -1.96 (0.31) *** | -1.93 (0.30) *** | |
| странаAUT | -0.94 (0.55) | ||
| странаBLR | -0.95 (0.53) | ||
| странаCAN | 1.13 (0.46) * | ||
| странаCZE | 0.56 (0.49) | ||
| странаDEN | -0.10 (0.56) | ||
| странаFIN | 0.20 (0.50) | ||
| странаFRA | -2.19 (0.69) ** | ||
| странаGER | -0.61 (0.51) | ||
| странаHUN | -0.61 (0.86) | ||
| странаITA | -3.58 (0.61) *** | ||
| странаJPN | -5.24 (0.71) *** | ||
| странаКАЗ | -1.16 (0.57) * | ||
| странаLAT | -1.38 (0.55) * | ||
| странаNOR | -1.61 (0.62) ** | ||
| странаPOL | 0.06 (1.12) | ||
| странаSLO | -1.55 (0.58) ** | ||
| странаSUI | -1.80 (0.53) *** | ||
| странаSVK | 1.44 (0.50) ** | ||
| странаSWE | 1.18 (0.48) * | ||
| странаUKR | -1.82 (0.59) ** | ||
| странаСША | 0.54 (0.45) | ||
| р 2 | 0.01 | 0.06 | 0.13 |
| Прил.
р 2 |
0.01 | 0.06 | 0.12 |
| Число.
обс.
|
3319 | 3319 | 3319 |
| RMSE | 5.40 | 5.27 | 5.10 |
| *** п < 0.001, ** п < 0.01, * п < 0.05 |
Интерпретация модели
Модель 1 .Увеличение когорты на один год соответствует увеличению роста хоккеистов на 0,1 см.
Коэффициент статистически значим, но модель объясняет только 1% вариации зависимой переменной.
В принципе, это не проблема, поскольку моделирование носит объяснительный характер и задача прогнозирования не ставится.
Однако низкий коэффициент детерминации указывает на то, что должны быть другие переменные, которые гораздо лучше объясняют разницу в росте между хоккеистами.
Модель 2 .
Защитники – самые высокие игроки в хоккее.
Вратари ниже на 2 см, нападающие на 2,6 см.
Все коэффициенты статистически значимы.
Объясняемая дисперсия зависимой переменной возрастает до 6%.
В этом случае коэффициент переменной когорта рождения не меняется.
Модель 3 .
Добавление переменных странового контроля интересно по двум причинам.
Во-первых, некоторые различия статистически значимы и интересны сами по себе.
Например, шведы, словаки и канадцы статистически значительно превосходят наших игроков.
Большинство наций значительно ниже нас: японцы на целых 5,2 см, итальянцы на 3,6 см, французы на 2,2 см (см.
также рис.
4).
Во-вторых, введение контрольных переменных для стран существенно снижает коэффициент при переменной когорта рождения - до 0,08. Это означает, что различия между странами частично объясняют различия по возрастным группам.
Коэффициент детерминации модели увеличивается до 13%.
код Р.
Рисунок 4. Рост числа хоккеистов по странам 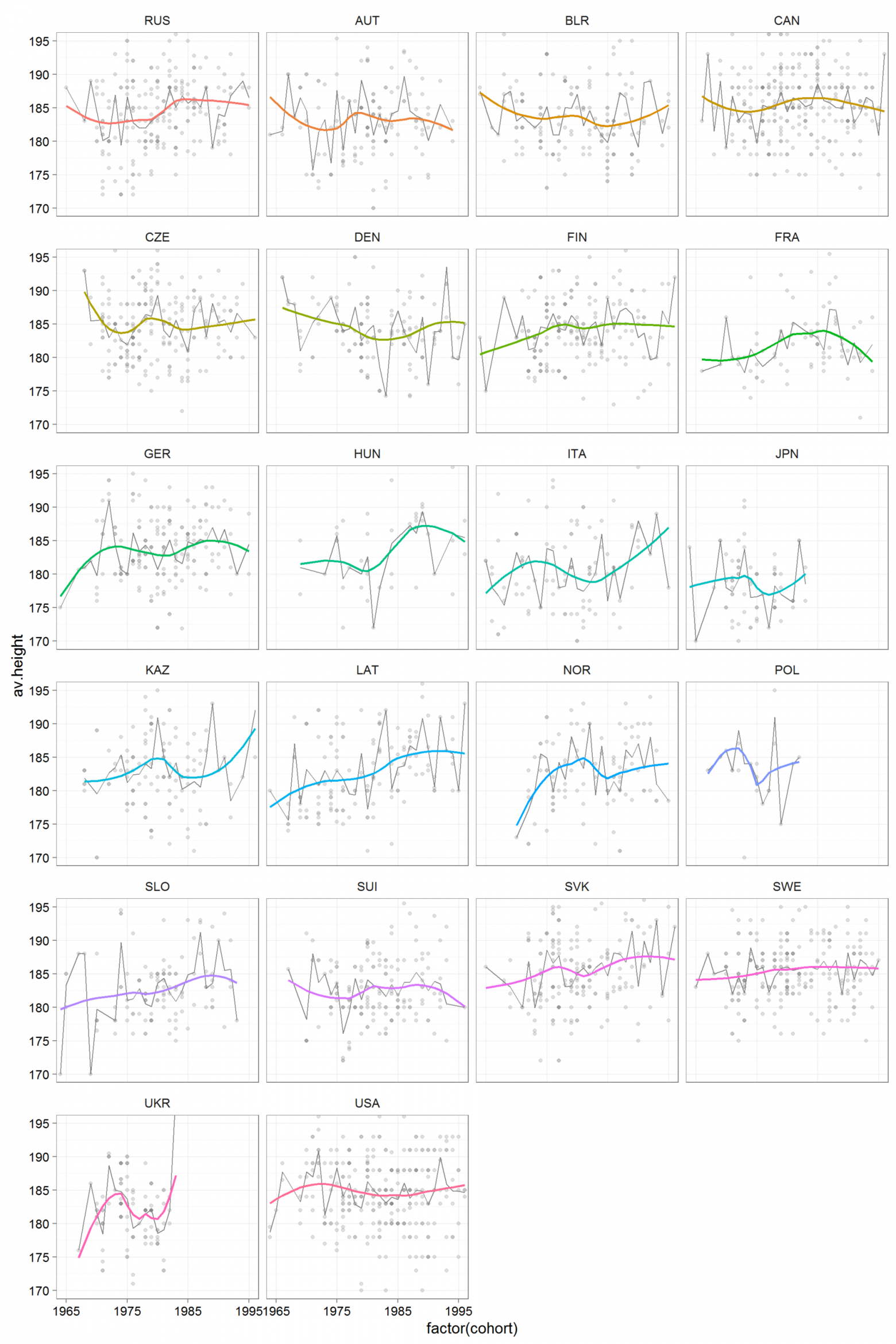
# players' height by country
gg_av.h_country <- ggplot(dfuc ,aes(x=factor(cohort),y=av.height))+
geom_point(color='grey50',alpha=.
25)+ stat_summary(aes(group=country),geom='line',fun.y = mean,size=.
5,color='grey50')+ stat_smooth(aes(group=country,color=country),geom='line',size=1)+ #geom_hline(yintercept = mean(height),color='red',size=.
5)+ facet_wrap(~country,ncol=4)+ coord_cartesian(ylim = c(170,195))+ scale_x_discrete(labels=paste(seq(1965,1995,10)),breaks=paste(seq(1965,1995,10)))+ theme_few(base_size = 15)+ theme(legend.position='none', panel.grid=element_line(colour = 'grey75',size=.
25))
Наиболее полная модель показывает, что хоккеисты увеличиваются в росте со скоростью 0,08 см в год. Это означает прирост на 0,8 см за десятилетие или 2,56 см за 32 года с 1964 по 1996 год. Заметим, что при учете контрольных переменных скорость увеличения роста хоккеистов оказывается примерно в полтора раза.
ниже, чем при более грубом анализе средних значений (рис.
1): 0,8 см за декаду против около 1,2 см.
Прежде чем мы наконец попытаемся понять, насколько значительна прибавка в высоте, хочу обратить ваше внимание еще на один интересный момент. Введение контрольных переменных предполагает фиксацию различий между категориями с единым наклоном линии регрессии (единым коэффициентом при основной объясняющей переменной).
Это не всегда хорошо и может маскировать значительные различия в силе взаимосвязей между переменными исследования в подвыборках.
Например, отдельное моделирование зависимости роста игроков от их амплуа (рис.
5) показывает, что связь наиболее выражена у вратарей и наименее заметна у защитников.
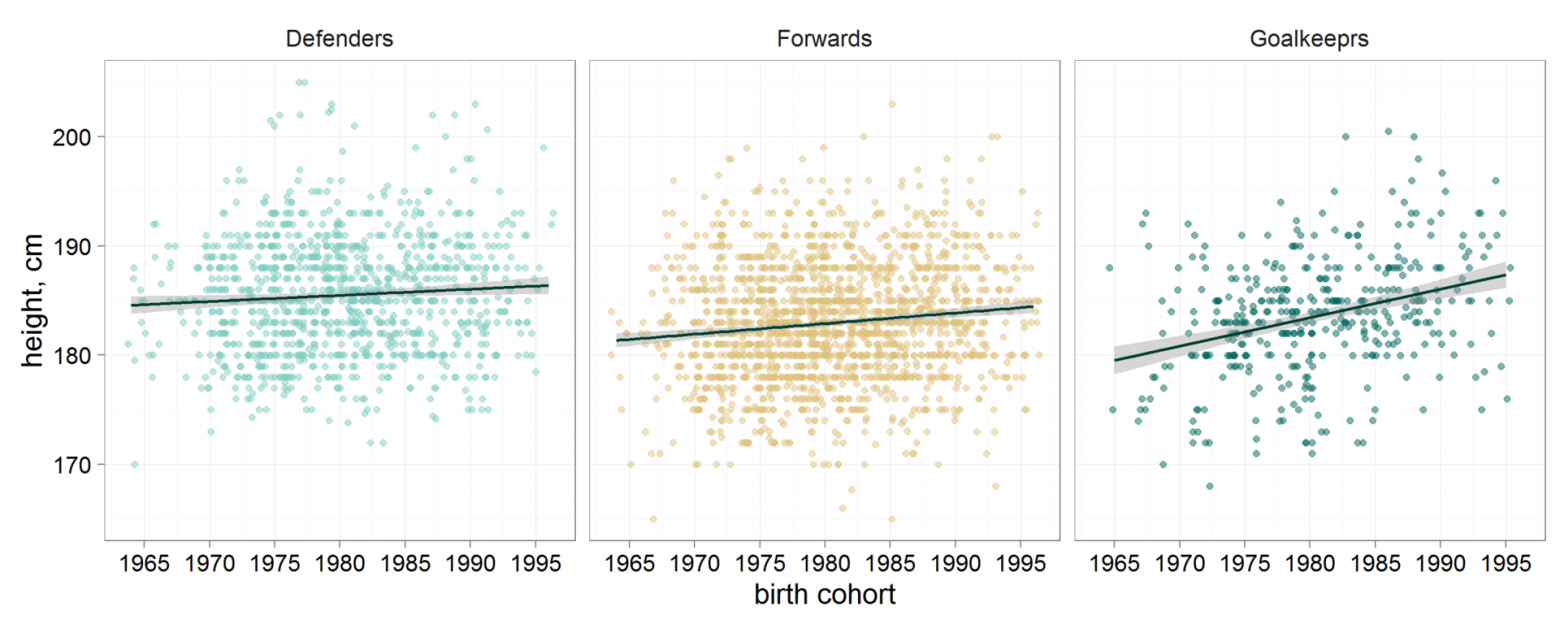
код Р.
Рисунок 5. Соотношение роста и когорты отдельно для защитников, нападающих и вратарей dfuc_pos <- dfuc
levels(dfuc_pos$position) <- c('Defenders','Forwards','Goalkeeprs')
gg_pos <- ggplot(dfuc_pos ,aes(x=cohort,y=av.height))+
geom_jitter(aes(color=position),alpha=.
5)+ stat_smooth(method = 'lm', se = T,color=brbg11[11],size=1)+ scale_x_continuous(labels=seq(1965,1995,5),breaks=seq(1965,1995,5))+ scale_color_manual(values = brbg11[c(8,4,10)])+ facet_wrap(~position,ncol=3)+ xlab('birth cohort')+ ylab('height, cm')+ theme_few(base_size = 20)+ theme(legend.position='none', panel.grid=element_line(colour = 'grey75',size=.
25))
код Р.
Таблица 3. Модель 3 отдельно для подвыборок защитников, нападающих и вратарей # separate models for positions
m3d <- lm(data = dfuc %>% filter(position=='D'),av.height~cohort+country)
m3f <- lm(data = dfuc %>% filter(position=='F'),av.height~cohort+country)
m3g <- lm(data = dfuc %>% filter(position=='G'),av.height~cohort+country)
htmlreg(list(m3d,m3f,m3g),file = '2016/160500 Hockey players/models_height_pos.html',single.row = T,
custom.model.names = c('Model 3 D','Model 3 F','Model 3 G'))
| Модель 3D | Модель 3Ф | Модель 3 Г | |
|---|---|---|---|
| (Перехват) | 108.45 (46.46) * | 49.32 (36.73) | -295.76 (74.61) *** |
| когорта | 0.04 (0.02) | 0.07 (0.02) *** | 0.24 (0.04) *** |
| странаAUT | 0.14 (0.96) | -2.01 (0.75) ** | 0.47 (1.47) |
| странаBLR | 0.30 (0.87) | -1.53 (0.73) * | -2.73 (1.55) |
| странаCAN | 1.55 (0.78) * | 0.39 (0.62) | 3.45 (1.26) ** |
| странаCZE | 0.87 (0.84) | 0.30 (0.67) | 0.63 (1.36) |
| странаDEN | -0.60 (0.95) | 0.10 (0.75) | -0.19 (1.62) |
| странаFIN | -0.55 (0.89) | -0.04 (0.67) | 2.40 (1.32) |
| странаFRA | -3.34 (1.15) ** | -2.06 (0.93) * | 1.39 (2.07) |
| странаGER | 0.48 (0.85) | -1.40 (0.72) | -0.65 (1.33) |
| странаHUN | -1.32 (1.47) | -0.70 (1.16) | 0.65 (2.39) |
| странаITA | -2.08 (1.08) | -4.78 (0.82) *** | -2.02 (1.62) |
| странаJPN | -4.13 (1.26) ** | -6.52 (0.94) *** | -2.27 (1.98) |
| странаКАЗ | -1.23 (0.95) | -1.82 (0.79) * | 1.79 (1.58) |
| странаLAT | -0.73 (0.95) | -1.39 (0.75) | -3.42 (1.49) * |
| странаNOR | -3.25 (1.07) ** | -1.06 (0.85) | -0.10 (1.66) |
| странаPOL | 0.82 (1.89) | -0.58 (1.55) | 0.37 (2.97) |
| странаSLO | -1.57 (0.99) | -1.54 (0.79) | -2.25 (1.66) |
| странаSUI | -1.98 (0.91) * | -2.36 (0.71) *** | 1.12 (1.47) |
| странаSVK | 2.94 (0.87) *** | 0.81 (0.67) | -0.70 (1.50) |
| странаSWE | 0.75 (0.81) | 1.24 (0.65) | 1.37 (1.33) |
| странаUKR | -1.37 (1.01) | -1.77 (0.80) * | -3.71 (1.66) * |
| странаСША | 0.76 (0.78) | -0.08 (0.62) | 2.58 (1.26) * |
| р 2 | 0.09 | 0.10 | 0.24 |
| Прил.
р 2 |
0.07 | 0.09 | 0.20 |
| Число.
обс.
|
1094 | 1824 | 401 |
| RMSE | 5.08 | 5.08 | 4.87 |
| *** п < 0.001, ** п < 0.01, * п < 0.05 |
За три десятилетия средний рост вратарей увеличился на 7 см! Пришло время сравнить эти изменения со средними показателями по численности населения.
Сравнение с населением
Результаты регрессионного анализа документируют значительные различия между странами.Поэтому имеет смысл сравнивать по странам: хоккеистов определенной страны с мужским населением этой же страны.
Чтобы сравнить рост хоккеистов со средним мужским населением, я использовал данные соответствующая научная статья ( PDF ).
Данные я скопировал из статьи (с помощью замечательной программы табула ) а также размещено в открытом доступе .
код Р.
Загрузка данных Hatton, T.J. и Bray, BE (2010) и подготовка к анализу.
# download the data from Hatton, T. J., & Bray, B. E. (2010).
# Long run trends in the heights of European men, 19th–20th centuries.
# Economics & Human Biology, 8(3), 405–413.
# http://doi.org/10.1016/j.ehb.2010.03.001
# stable URL, copied data ( https://dx.doi.org/10.6084/m9.figshare.3394795.v1 )
df_hb <- read.csv(' https://ndownloader.figshare.com/files/5303878 ')
df_hb <- df_hb %>%
gather('country','h_pop',2:16) %>%
mutate(period=paste(period)) %>%
separate(period,c('t1','t2'),sep = '/')%>%
transmute(cohort=(as.numeric(t1)+as.numeric(t2))/2,country,h_pop)
# calculate hockey players' cohort height averages for each country
df_hoc <- dfu %>% group_by(country,cohort) %>%
summarise(h_hp=mean(av.height)) %>%
ungroup()
К сожалению, данные по динамике роста населения совпадают только с 8 странами из моего хоккейного набора данных: Австрия, Дания, Финляндия, Франция, Германия, Италия, Норвегия, Швеция.
код Р.
Перекрывающиеся данные # countries in both data sets
both_cnt <- levels(factor(df_hb$country))[which(levels(factor(df_hb$country)) %in% levels(df_hoc$country))]
both_cnt
код Р.
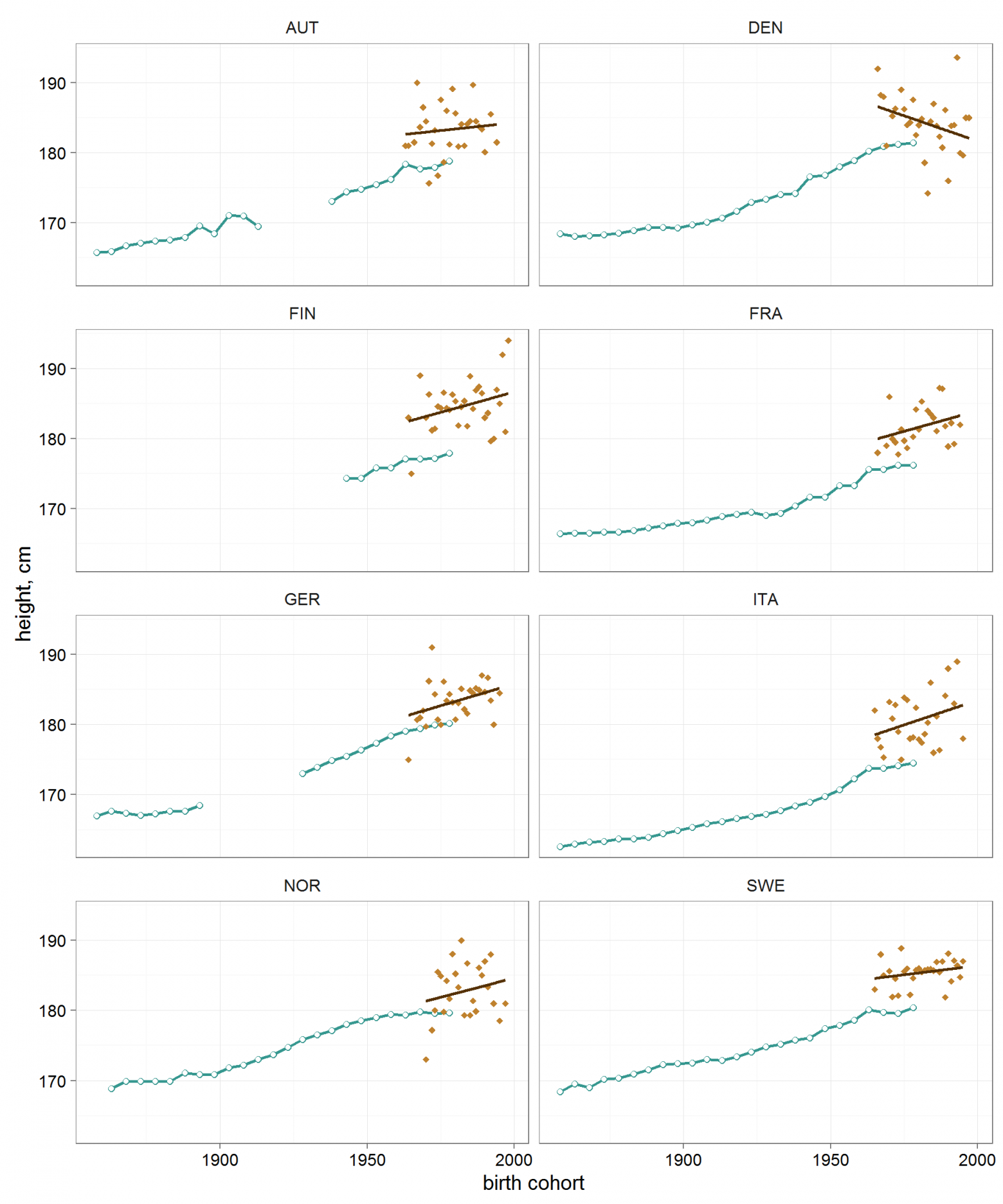
Рисунок 6. Сравнение динамики роста мужского населения и хоккеистов.
Примечание: зеленый цвет – мужское население; коричневый цвет – хоккеисты.
gg_hoc_vs_pop <- ggplot()+
geom_path(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color=brbg11[9],size=1)+
geom_point(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color=brbg11[9],size=2)+
geom_point(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color='white',size=1.5)+
geom_point(data = df_hoc %>% filter(country %in% both_cnt), aes(x=cohort,y=h_hp),
color=brbg11[3],size=2,pch=18)+
stat_smooth(data = df_hoc %>% filter(country %in% both_cnt), aes(x=cohort,y=h_hp),
method='lm',se=F,color=brbg11[1],size=1)+
facet_wrap(~country,ncol=2)+
ylab('height, cm')+
xlab('birth cohort')+
theme_few(base_size = 15)+
theme(panel.grid=element_line(colour = 'grey75',size=.
25))
Во всех анализируемых странах хоккеисты выше среднестатистических мужчин на 2-5 см.
Но это неудивительно – в спорте существует значительный отбор.
Примечательно и другое.
В развитых странах мира особенно быстрый рост мужского населения произошел в первой середине 20 века.
В когортах, родившихся примерно в 1960-х годах, рост мужчин приблизился к плато и начал быстро увеличиваться.
Тенденция среднего роста хоккеистов во всех странах (за исключением почему-то Дании), казалось, продолжала приостановленную многолетнюю тенденцию всего мужского населения.
Для когорт европейцев, родившихся в первой половине XX века, темпы увеличения среднего роста варьировали от 1,18 до 1,74 см за десятилетие в зависимости от страны (рис.
7).
С 1960-х годов этот показатель снизился до уровня 0,15-0,80 за 10 лет. 
код Р.
Рисунок 7. Средняя динамика роста мужского населения # growth in population
df_hb_w <- df_hb %>% spread(cohort,h_pop)
names(df_hb_w)[2:26] <- paste('y',names(df_hb_w)[2:26]
Теги: #хоккей #Сборная России #Чемпионат мира по хоккею 2016 #регрессия #рост спортсмена #ИИХФ #Открытые данные #спортивная аналитика #r #Визуализация данных #исследовательский анализ данных #когортный анализ #когортный эффект #когортный анализ #когортный эффект #программирование # Интеллектуальный анализ данных #r #Открытые данные #Визуализация данных

-
Эффективное Преобразование Pdf В Текст
19 Oct, 24 -
Telehouse Caravan: Хостинг Для Богатых
19 Oct, 24 -
Идеальная Производительность Http
19 Oct, 24 -
Yotaphone 2: Инновации И Безопасность
19 Oct, 24


