Французский учёный и архитектор Клод Перро, брат знаменитого сказочника Шарля Перро, изобрел оригинальное счётное устройство — рабдологические счёты.
Счетная машина стала ценным дополнением 17–18 веков, периода, весьма богатого изобретением счетных устройств.

Клод Перро (1613-1688)
Перро дал своему изобретению имя в духе античных времен, когда счетами называлась небольшая дощечка, на которой записывались числа.
А поскольку машина производила арифметические действия с помощью маленьких палочек с цифрами, ее считали рабдологической.

Римские счеты
Впервые устройство упоминается в книге Клода Перро «Собрание большого числа машин собственного сочинения» (1700), изданной посмертно.
В сборнике содержались описания почти всех изобретений автора («маятниковые часы», «машина для поднятия тяжестей», «машина для повышения эффективности огнестрельного оружия» и др.
).
Рабдологические счеты значились на десятом месте.
Это была компактная и простая вычислительная машина, вошедшая в историю благодаря своему существенному отличию от других изобретенных устройств в своей области.
Вместо обычных шестерен Паскаля в рабдологических счетах использовались зубчатые рейки (рейки).
Счетная машина имела форму пластины толщиной с палец, высота достигала примерно 30 см, а ширина – 14 см.
На лицевой стороне устройства были вырезаны два окошка, куда выводились результаты.
В верхнем окне отображался результат вычитания, а в нижнем — сложения.
Внизу аверса была выгравирована таблица умножения.

Кроме того, на лицевой стороне было вырезано семь борозд, вдоль которых располагались чешуи с делениями 1, 2, 3, 4, 5, 6, 7, 8, 9. Линейки располагались в пазах.
С помощью булавки с заостренным кончиком они перемещались вверх и вниз к основанию устройства.
Глубокие знаки делили каждую строку на 26 частей.
В метки вставлялся кончик булавки, что позволяло перемещать линейки с легкостью и необходимой точностью.
В одиннадцати верхних делениях линейки существовала возрастающая последовательность (0,1,2,3,4,5,6,7,8,9,0) для вычитания.
Нижние одиннадцать подразделений содержали убывающую последовательность (0,9,8,7,6,5,4,3,2,1,0).
Соответственно, его использовали для сложения.
Номера этих последовательностей были показаны в окнах результатов.
В нижнем окне это было желаемое значение сложения, а в верхнем окне — желаемое значение вычитания.
Последовательности, отмеченные на линейках, были отделены друг от друга четырьмя пустыми делениями.

В сумке устройство использовало семь линеек, которые были отделены друг от друга тонкими пластинами.
Строки располагались в порядке возрастания.
Крайняя правая линия символизировала ранг единиц, следующая за ней линия представляла ранг десятков, затем сотен и так далее до ранга миллионов.
Каждая пластина, отделявшая линейки друг от друга, имела отверстие.
Он служил для перевода переполнения из младшего разряда в старший и располагался у основания линейки, перенесенной на самый верх устройства.
Размер отверстия достигал трех делений линейки.
Каждая линейка имела 11 зубцов у основания правой стороны, по одному на деление.
На другой стороне линейки (если считать снизу – под 11-м и 12-м делением) находился подпружиненный крючок.
Зубцы и крючок использовались для переноса переполнения от младшей к старшей цифре.

Перевод из младших в старшие чины происходил следующим образом.
Когда младшая полоска находилась вверху прибора (то есть в окнах результатов сложения и вычитания были нули), подпружиненный крючок был спрятан в корпусе линейки, упираясь в пластину, расположенную к слева от него.
Когда линейка опустилась, подпружиненный крючок приблизился к отверстию в пластине.
Когда в окне результатов сложения появилась цифра 7, принадлежащая перемещаемой линейке, подпружиненный крючок начал двигаться в отверстие стержня, и в тот момент, когда в окне результатов появилась цифра 9, он зацепился с зубы правителя высочайшего порядка.
Впоследствии движение правителя низшей категории переместило правителей старшей категории.
В результате, когда в окне результатов сложения появилась цифра 0 младшей линии, следующая за цифрой 9, старшая линия переместилась ровно на одно деление вниз за счет зацепления крючка с зубьями.
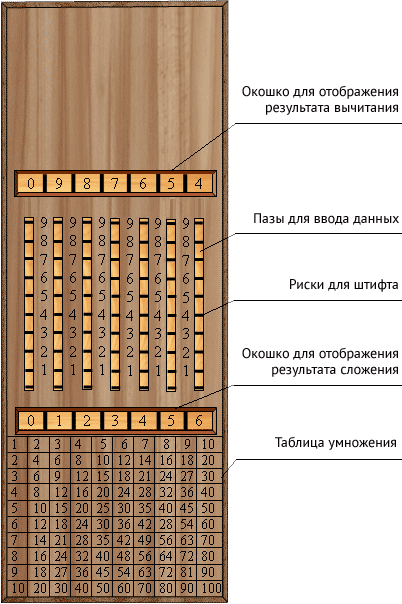
Пример операции сложения 127+65
Шаг 1. Сначала все цифры рабдологических счетов устанавливаются на 0. Для этого булавкой переведите линейки в самое верхнее положение.
Шаг 2. Штифт помещается в паз на отметке линии второстепенного разряда, расположенной напротив цифры 7. Линейка перемещается до тех пор, пока штифт не упрется в нижний конец паза.
В этом случае введенное число 7 отобразится в окне результата сложения в младшей цифре.
Важным моментом является то, что в окне результата вычитания в младшей цифре будет отображаться число, необходимое для дополнения семи до десяти, то есть число 3. Шаг 3. Аналогичную операцию продолжают с цифрой десятки, только в этом случае паз устанавливается напротив цифры 2. Шаг 4. Для места сотни желобок устанавливается напротив цифры 1. Далее паз перемещается вниз до упора, то есть на одно деление.
В окне результатов сложения отобразится число 127. Шаг 5. Следующим шагом будет ввод второго члена.
Штифт устанавливается в паз на линейной отметке второстепенного разряда, расположенной напротив цифры 5, линейка перемещается вниз до упора.
В этом случае штифт остановится напротив цифры 2, так как линейка упрется в нижнюю стенку устройства раньше, чем штифт достигнет нижнего конца паза.
При этом линейка десятков сместится на одно деление вниз за счет срабатывания механизма переноса переполнения.
В окне результатов сложения отобразится число 130. Шаг 6. Чтобы получить на месте единиц правильное число – 2, следует, не вынимая штифт из прорези, переместить линейку вверх до тех пор, пока штифт не упрется в конец паза.
Таким образом, в окне результата сложения отобразится число 132. Шаг 7. Заключительный этап – вводится место десятков второго члена.
Для этого штифт устанавливают в паз на отметке линейки десятков, расположенной напротив цифры 6, линейку перемещают вниз до упора.
На этом расчеты завершены, и в окне результатов сложения отобразится искомое значение: 192. Пример операции вычитания 68-23 Шаг 1. Все цифры рабдологических счетов ставят на 0. Для этого с помощью булавки линейки переводят в самое верхнее положение.
Шаг 2. Вводится младшая значащая цифра уменьшаемого.
Линейка младшей значащей цифры перемещается так, чтобы в окне результата вычитания на позиции младшей цифры отображалась цифра 8. Для этого необходимо поместить штифт в паз на отметке напротив цифры 2 и переместить линейку вниз до тех пор, пока штифт не упрется в торцевой паз.
Шаг 3. Далее вводится разряд десятков уменьшаемого, для чего соответствующая линейка перемещается так, чтобы в окне результата вычитания на второй позиции отобразилось число 6. Для этого штифт помещают в паз на отметке, расположенной напротив цифры 4, и перемещают линейку вниз до тех пор, пока штифт не упрется в конец паза.
В результате в окне результатов вычитания отобразится число 68. Шаг 4. Вычитаемое при сложении вводится так же, как и слагаемое.
Для ввода младшей значащей цифры вычитаемого штифт устанавливают в паз на отметке линейки младшей цифры, напротив цифры 3. Линейка перемещается вниз до тех пор, пока штифт не упрется в конец паза.
Далее вводится самая старшая цифра вычитаемого, для чего штифт устанавливается в паз на отметке второй линейки слева, напротив цифры 2. Линейка перемещается вниз до тех пор, пока штифт не упрется в конец вычитаемого.
канавка.
Разница между двумя числами находится, и в окне результата вычитания отображается искомый результат: 45. 
При вычитании на рабдологических счетах применялся прием десятичных чисел, аналогичный методу, использованному в Паскалине.
В качестве примера решение уравнения: Y=68-23=45. Используя метод сложения, число 68 представляется как разность чисел 100 и 32 (68=10-32).
В результате уравнение сводится к следующему виду: Y=68-23=100-32-23=100-(32+23)=27. Такое преобразование заменяет вычитание сложением и вычитанием результата сложения из 100, что является обратным преобразованием сложения.
Следовательно, остается решить задачу автоматического сложения до десяти, для чего на всех линейках напечатаны две последовательности чисел, а на крышке рабдологических счетов имеются два окошка для отображения результата, расположенные так, чтобы суммы два числа, отображаемые в окнах и расположенные одно под другим, всегда равны десяти.
В своей конструкции Перро использовал элементы, которые впервые использовал шотландский математик Джон Непер в простом умножающем устройстве.
Он предназначался для умножения, деления, извлечения квадратного корня и был подробно описан Непером в последней при его жизни публикации («Rabdologia seu Numerationis», 1617).

палочки Напьера
Описание рабдологических счетов показывает их отличие от существовавших в то время вычислительных машин.
И, что немаловажно, устройством было достаточно просто пользоваться.
Однако рабдологические счеты не получили должного признания.
Возможно, из-за ненадежности подпружиненного крюкового устройства (оно использовалось не только для переноса, но и для фиксации планок в положениях, соответствующих введенным цифрам), которое часто выходило из строя при постоянном использовании.
Но если реализованное изобретение не получило широкого применения на практике, то идеи Перро впоследствии нашли применение в других простых и надежных счетных устройствах («Числитель Куммера», «Счетчик Ганса Забельного» и др.
).

«Счетчик Куммера» (1846 г.
)
P.S. Специально для читателей Хабра мы проводим акцию.
Пишите с подробностями здесь .
Теги: #математика #устройства #технологии #обратное проектирование #изобретения #вычислительные машины #вычислительные машины #уравнения #уравнения

-
Преобразование Изображений В Компьютерах
19 Oct, 24 -
Килби, Джек Ст-Клер
19 Oct, 24 -
Пятница: Безопасность И Парадокс Выжившего
19 Oct, 24 -
Парадокс Дня Рождения
19 Oct, 24 -
Продюсеров Видеозаписи Обвинили В Заговоре
19 Oct, 24 -
Январский Рейтинг Языков Программирования
19 Oct, 24


