Понимая, что я давно не писал на Хабре ничего полезного про FP и Haskell, и что для технической статьи есть вполне отличный повод, я решил стряхнуть былые времена.
В статье пойдет речь Программная транзакционная память (STM) , который мне удалось реализовать на монадах Free с участием ADT (алгебраических типов данных) и MVars (конкурентных изменяемых переменных).
И вообще, Proof of Concept оказался предельно простым по сравнению с «настоящим» STM. Давайте обсудим это.
Программная транзакционная память
STM — это подход к программированию конкурентной модели данных.Параллелизм здесь заключается в том, что разные части модели могут обновляться в разных потоках независимо друг от друга, а конфликты на общих ресурсах разрешаются с помощью транзакций.
Транзакционность аналогична базе данных, но есть ряд отличий.
Допустим, вы хотите изменить некоторые данные в своем коде.
Концептуально вы можете думать о своем коде как о том, что он не пишется непосредственно в модель, а работает с копией той части, которая ей нужна.
В конце движок STM открывает транзакцию и сначала проверяет, что интересующая вас часть модели никем не была изменена.
Разве оно не изменилось? Хорошо, новые значения будут записаны.
Кто-то добрался туда до тебя? Это конфликт. Пожалуйста, перезапустите расчеты на новых данных.
Схематически это можно представить так: 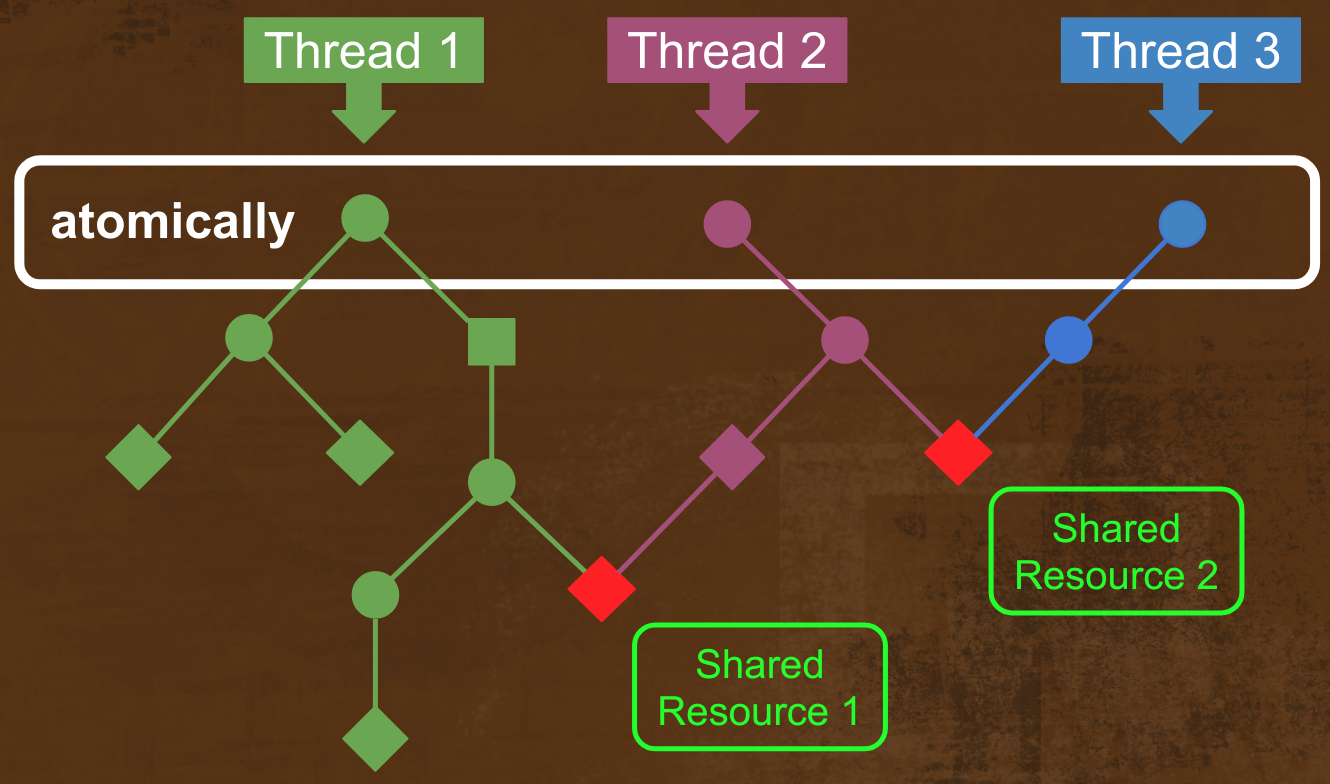
Здесь атомарные операции выполняются потоками параллельно, но фиксируются только внутри транзакций, которые блокируют доступ к изменяемым частям модели.
Существуют разные вариации СТМ, но мы поговорим конкретно о той, которая предложена в известной работе.
«Транзакции составной памяти» , ведь он отличается рядом замечательных свойств:
- разделены понятия модели данных и вычислений на ней;
- Вычисление является монадой STM и компонуется в полном соответствии с парадигмой FP;
- есть концепция ручного перезапуска расчета (retry);
- наконец, есть отличная реализация для Haskell, которую я, правда, рассматривать не буду, а остановлюсь на своей, похожей по интерфейсу.
Вы можете преобразовать любую вашу обычную модель в транзакционную; для этого библиотеки STM предоставляют различные примитивы: переменные ( ТВар ), очереди ( TQueue ), массивы ( TArray ) и многие другие.
Нетрудно догадаться, что транзакционные переменные — TVars («существа») — уже минимально достаточны для полноценного STM, а все остальное выражается через них.
Рассмотрим, например, проблема обедающих философов .
Мы можем думать о форках как об общем ресурсе, к которому нам нужно создать конкурентный доступ:
Эта модель самая простая: каждый форк хранится в своей переменной транзакции, и работать с ними нужно парами: (вилка1, вилка2), (вилка2, вилка3), … (вилка5, вилка1) .data ForkState = Free | Taken type TFork = TVar ForkState data Forks = Forks { fork1 :: TFork , fork2 :: TFork , fork3 :: TFork , fork4 :: TFork , fork5 :: TFork }
Но такая структура будет работать хуже: type Forks = TVar [ForkState]
Потому что общий ресурс всего один, и если бы у нас было пять философствующих тредов, они бы получили право на коммит один за другим.
В результате обедал бы только один философ, а думали бы четверо других, а в следующий раз обедал бы другой, но тоже один, хотя теоретически с пятью вилками могли бы обедать параллельно двое.
Поэтому необходимо создать конкурентоспособную модель, которая будет давать наиболее ожидаемое поведение.
Вот как может выглядеть расчет в монаде STM для модели с отдельными существами-вилками: data ForkState = Free | Taken
type TFork = TVar ForkState
takeFork :: TFork -> STM Bool
takeFork tFork = do
forkState <- readTVar tFork
when (forkState == Free) (writeTVar tFork Taken)
pure (forkState == Free)
Функция возвращает Истинный , если форк был свободен и его успешно «взяли», то есть перезаписали тфорк .
Ложью будет, если вилка уже используется и к ней нельзя прикоснуться.
Теперь давайте посмотрим на пару вилок.
Ситуаций может быть пять:
- Оба бесплатны
- Левый занят (левый сосед), правый свободен
- Левый свободен, правый занят (правым соседом)
- Оба заняты (соседями)
- Оба заняты (нашим философом)
takeForks :: (TFork, TFork) -> STM Bool
takeForks (tLeftFork, tRightFork) = do
leftTaken <- takeFork tLeftFork
rightTaken <- takeFork tRightFork
pure (leftTaken && rightTaken)Вы можете заметить, что код позволяет взять одну развилку (например, левую), но не взять другую (например, правую, которая оказывается занята соседом).
Функция взятьВилки конечно вернусь ЛОЖЬ в данном случае, а как быть с тем, что одна вилка оказалась в руках нашего философа? Он не сможет есть один, поэтому ему нужно положить его обратно и еще некоторое время подумать.
После этого можно попробовать еще раз в надежде, что оба форка окажутся бесплатными.
Но «возвращение назад» в рамках СТМ реализуется несколько иначе, чем в рамках других конкурентных структур.
Мы можем считать, что обе переменные - tLeftFork И tRightFork - это локальные копии, не связанные с одним и тем же ресурсом у других философов.
Поэтому можно не «поставить» вилку обратно, а сказать расчету, что она не удалась.
Тогда наш один взятый форк не будет записан в общие ресурсы - это все равно, как если бы не было успешного вызова взять вилку .
Это очень удобно, и именно операция «отмены» текущего монадического вычисления отличает реализацию Haskell STM от других.
Существует специальный метод отмены.
повторить попытку , давай перепишем взятьВилки используй это: takeForks :: (TFork, TFork) -> STM ()
takeForks (tLeftFork, tRightFork) = do
leftTaken <- takeFork tLeftFork
rightTaken <- takeFork tRightFork
when (not leftTaken || not rightTaken) retry
Расчет будет успешным, если наш философ взял обе вилки одновременно.
В противном случае он будет перезагружаться снова и снова через определенные промежутки времени.
В этой версии мы не возвращаемся Бул , потому что нам не нужно знать, были ли оба ресурса успешно получены.
Если функция выполнилась и расчет не завершился неудачей, значит, он прошел успешно.
После того, как мы взяли вилки, нам, вероятно, нужно будет сделать что-то еще, например, перевести философа в состояние «Еда».
Мы просто делаем это после звонка взятьВилки , а монада STM будет следить за согласованностью состояний «существ»: data PhilosopherState = Thinking | Eating
data Philosopher = Philosopher
{ pState :: TVar PhilosopherState
, pLeftFork :: TFork
, pRrightFork :: TFork
}
changePhilosopherActivity :: Philosopher -> STM ()
changePhilosopherActivity (Philosopher tState tLeftFork tRightFork) = do
state <- readTVar tState
case state of
Thinking -> do
taken <- takeForks tFs
unless taken retry -- Do not need to put forks if any was taken!
writeTVar tAct Eating
pure Eating
Eating -> error "Changing state from Eating not implemented."
Полную реализацию этого метода мы оставим в качестве упражнения, а теперь посмотрим на последнее недостающее звено.
До сих пор мы описывали только логику модели транзакций, но не конкретизировали ее.
ТВар мы еще ничего не создали и не запустили.
Давай сделаем это: philosoperWorker :: Philosopher -> IO ()
philosoperWorker philosopher = do
atomically (changePhilosopherActivity philosopher)
threadDelay 5000
philosoperWorker philosopher
runPhilosophers :: IO ()
runPhilosophers = do
tState1 <- newTVarIO Thinking
tState2 <- newTVarIO Thinking
tFork1 <- newTVarIO Free
tFork2 <- newTVarIO Free
forkIO (philosoperWorker (Philosopher tState1 tFork1 tFork2))
forkIO (philosoperWorker (Philosopher tState2 tFork2 tFork1))
threadDelay 100000
Комбинатор атомарно :: STM a -> IO a выполняет расчет в монаде СТМ атомарно.
По типу видно, что чистая часть — работа с конкурентной моделью — отделена от нечистых вычислений в монаде.
ИО .
Код STM не должен иметь никакого эффекта.
Лучше - вообще никакой, иначе при перезагрузках вы получите какие-то странные результаты, например, если вы писали в файл, то в некоторых ситуациях вы можете получить ложные записи, и эту ошибку очень сложно отловить.
Поэтому можно предположить, что в монаде СТМ есть только чистые вычисления, и их выполнение — атомарная операция, которая, однако, не блокирует другие вычисления.
Функции создания тоже нечистые.
TVar newTVarIO :: a -> IO (TVar a) , но ничто не мешает вам создавать новые ТВар внутри СТМ использование чистого комбинатора newTVar :: a -> STM (TVar a) .
Нам это просто было не нужно.
Внимательные заметят, что общим ресурсом здесь являются лишь развилки, а состояние самих философов завернуто в ТВар просто для удобства.
Подведем итог.
Минимальная реализация СТМ должен содержать следующие функции для работы с ТВар : newTVar :: a -> STM (TVar a)
readTVar :: TVar a -> STM a
writeTVar :: TVar a -> a -> STM ()
Выполнение расчетов: atomically :: STM a -> IO a
Наконец, огромным плюсом будет возможность перезапустить расчет: retry :: STM a
Конечно, в библиотеках есть огромное количество других полезных конструкций, например экземпляр класса типа Альтернатива Для СТМ , но оставим это для самостоятельного изучения.
STM на свободных монадах
Реализация корректно работающего STM считается сложной задачей, и лучше, если будет поддержка со стороны компилятора.Я слышал, что реализации в Haskell и Clojure на данный момент являются лучшими, а в других языках STM не совсем реален.
Можно предположить, что монадические СТМ с возможностью перезапуска вычислений и управления эффектами не существуют ни в одном императивном языке.
Но это все праздные предположения, и я могу ошибаться.
К сожалению, я даже не понимаю внутренностей библиотеки Haskell. стм , не говоря уже о других экосистемах.
Однако с точки зрения интерфейса совершенно ясно, как код должен вести себя в многопоточной среде.
И если есть спецификация интерфейса (предметно-ориентированный язык) и ожидаемое поведение, этого уже достаточно, чтобы попытаться создать свой STM с использованием Free монад. Так, Свободные монады .
Любой DSL, построенный на свободных монадах, будет иметь следующие характеристики:
- Чистый DSL, скомпилированный монадически, то есть по-настоящему функциональный;
- Код на таком DSL не будет содержать ничего лишнего, кроме предметной области, а значит, его будет легче читать и понимать;
- Интерфейс и реализация фактически разделены;
- Реализаций может быть несколько, и их можно заменять во время выполнения.
На мой взгляд, любую проблему в домене можно решить и с помощью Free-monadic DSL. Поскольку эта тема очень широка и затрагивает многие вопросы проектирования и архитектуры программного обеспечения в функциональном программировании, я оставлю другие детали в стороне.
Желающие могут обратиться к многочисленным источникам в Интернете или к моей полукниге.
«Функциональный дизайн и архитектура» , где Свободным монадам уделяется особое внимание.
Теперь давайте посмотрим на код моей библиотеки без stm .
Поскольку STM — предметно-ориентированный язык создания транзакционных моделей, он чистый и монадический, то можно предположить, что для минимального STM Free DSL должен содержать те же методы для работы с TVar, и они будут автоматически компонуемы и чисты в эта самая Свободная-монада.
Сначала давайте определим, что такое TVar. type UStamp = Unique
newtype TVarId = TVarId UStamp
data TVar a = TVar TVarId
Нам нужно будет дифференцировать наших «тварей», чтобы каждый экземпляр был идентифицирован по уникальному значению.
Пользователю библиотеки это знать не обязательно; он будет ожидать использования типа ТВар а .
Работа со значениями такого типа — это половина всего поведения нашего маленького STM. Поэтому мы определяем А.
Д.
Т.
соответствующими методами: data STMF next where
NewTVar :: a -> (TVar a -> next) -> STMF next
WriteTVar :: TVar a -> a -> next -> STMF next
ReadTVar :: TVar a -> (a -> next) -> STMF next
И здесь нужно остановиться подробнее.
Почему мы должны это делать? Суть в том, что монада Free должна быть построена поверх какого-то eDSL. Самый простой способ определить это — определить возможные методы как конструкторы ADT. Конечный пользователь не будет работать с этим типом, но мы будем использовать его для интерпретации методов с некоторым эффектом.
Очевидно, что метод NewTVar следует интерпретировать с результатом «создается новый TVar и возвращается как результат».
Но можно сделать интерпретатор, который будет делать что-то еще, например, писать в базу данных, в журнал или даже совершать обращения к реальному STM. Эти конструкторы содержат всю необходимую информацию для интерпретации.
Конструктор НовыйTVar содержит некоторое пользовательское значение а , и при интерпретации мы подставим это значение в новый TVar. Но проблема в том, что а должно быть разным для каждого вызова НовыйTVar .
Если бы мы просто написали STMF следующий , а уже было бы общим для всего кода, где связано несколько вызовов НовыйTVar : data STMF next a where
NewTVar :: a -> (TVar a -> next) -> STMF next
Но это бессмысленно, потому что мы все равно хотим использовать НовыйTVar для своих произвольных типов и чтобы они не давили друг на друга.
Вот почему мы убираем а в локальную видимость только конкретного метода.
Примечание .Что это за поле? следующий в том, что? Здесь мы сталкиваемся с требованием монады Free. Ей нужно где-то хранить продолжение текущего метода, и просто поле следующий она не удовлетворена — ADT должен быть функтором над этим полем.Фактически, чтобы ускорить работу над доказательством концепции, введите а У меня есть ограничение на сериализуемость (экземпляр класса ТоJSON/ИзJSON из библиотеки Эсон ).
Дело в том, что мне нужно будет хранить в карте эти разные типы ТВаров, но я не хочу возиться с Типизированный/динамический или, тем более, с HL-списки .
В реальном типе STM а Это может быть абсолютно что угодно, даже функции.
Этим вопросом я тоже займусь когда-нибудь позже.
Да, метод НовыйTVar должен вернуться ТВар а , и мы видим, что продолжение (TVar a -> следующий) просто ждет нашей новой входной переменной.
На другой стороне, WriteTVar не возвращает ничего полезного, поэтому продолжение имеет тип следующий , - то есть он ничего не ожидает на входе.
Создайте тип функтора СТМФ не сложно: instance Functor STMF where
fmap g (NewTVar a nextF) = NewTVar a (g .
nextF) fmap g (WriteTVar tvar a next ) = WriteTVar tvar a (g next) fmap g (ReadTVar tvar nextF) = ReadTVar tvar (g .
nextF)
Более интересный вопрос — где находится наша собственная монада для STM. Вот она: type STML next = Free STMF next
Мы завернули тип СТМФ в типе Бесплатно , а вместе с ним появились и все необходимые нам монадические свойства.
Остается только создать ряд удобных монадических функций поверх наших голых языковых методов.
СТМФ : newTVar :: ToJSON a => a -> STML (TVar a)
newTVar a = liftF (NewTVar a id)
writeTVar :: ToJSON a => TVar a -> a -> STML ()
writeTVar tvar a = liftF (WriteTVar tvar a ())
readTVar :: FromJSON a => TVar a -> STML a
readTVar tvar = liftF (ReadTVar tvar id)
В результате мы уже можем оперировать транзакционной моделью в виде ТВаров.
На самом деле, можно взять пример обедающих философов и просто заменить СТМ на СТМЛ : data ForkState = Free | Taken
type TFork = TVar ForkState
takeFork :: TFork -> STML Bool
takeFork tFork = do
forkState <- readTVar tFork
when (forkState == Free) (writeTVar tFork Taken)
pure (forkState == Free)
Легкая победа! Но есть вещи, которые мы пропустили.
Например, способ прекращения вычислений повторить попытку .
Легко добавить: data STMF next where
Retry :: STMF next
instance Functor STMF where
fmap g Retry = Retry
retry :: STML ()
retry = liftF Retry
Моя библиотека имеет незначительные отличия от своей старшей сестры; в частности метод повторить попытку возвращается сюда Единица , хотя он должен возвращать произвольный тип а .
Это не фундаментальное ограничение, а артефакт быстрой разработки PoC, и я исправлю это в будущем.
Однако даже этот код останется без изменений, кроме замены самой монады: takeForks :: (TFork, TFork) -> STML ()
takeForks (tLeftFork, tRightFork) = do
leftTaken <- takeFork tLeftFork
rightTaken <- takeFork tRightFork
when (not leftTaken || not rightTaken) retry
Монадический eDSL максимально похож на базовую реализацию, но запуск скриптов STML отличается.
Мой комбинатор атомарно , в отличие от базовой реализации, принимает дополнительный аргумент — контекст, в котором будет происходить вычисление.
atomically :: Context -> STML a -> IO a
Контекст хранит пользовательские данные в виде TVar, поэтому вы можете иметь несколько разных контекстов.
Это может быть полезно, например, для разделения моделей транзакций, чтобы они не влияли друг на друга.
Допустим, в одной модели создается огромное количество пользовательских данных, а в другой модели набор TVar вообще не меняется.
Тогда имеет смысл разделить контексты, чтобы вторая модель не испытывала проблем при выполнении из-за «раздутия» соседа.
В базовой реализации контекст глобальный, и я не очень понимаю, как это можно обойти.
Код запуска философов теперь выглядит так: philosoperWorker :: Context -> Philosopher -> IO ()
philosoperWorker ctx philosopher = do
atomically ctx (changePhilosopherActivity philosopher)
threadDelay 5000
philosoperWorker ctx philosopher
runPhilosophers :: IO ()
runPhilosophers = do
ctx <- newContext
Теги: #stm #haskell #free-monads #monads #haskell #Параллельное программирование #Функциональное программирование

-
Преимущества Ремонта Экранов Ноутбуков
19 Oct, 24 -
Работа На Дому Повышает Производительность
19 Oct, 24


