Привет, Хабр! В этом посте мы хотим поделиться нашим решением проблемы прогнозирования скрытых связей в корпоративной социальной сети «Улей» компании «Билайн».
Эту проблему мы решили в рамках виртуального хакатона Майкрософт .
Надо сказать, что до этого хакатона наша команда уже имела успешный опыт решения подобных задач на хакатоне от Одноклассники и нам очень хотелось протестировать наши разработки на новых данных.
В этой статье мы поговорим об основных подходах, которые используются для решения подобных задач, и поделимся деталями нашего решения.
Постановка задачи и исходные данные
Разработка качественного алгоритма рекомендации друзей — одна из наиболее приоритетных задач практически для любой социальной сети, потому что… Функционал такого типа — мощный инструмент привлечения и удержания пользователей.Публикаций на эту тему в англоязычной литературе довольно много, а само задание даже имеет специальную аббревиатуру PYMK (People You May Know).
Компания Билайн внутри виртуальный хакатон от Microsoft предоставил график корпоративной социальной сети «Улей».
5% ребер графа были искусственно скрыты.
Задача заключалась в том, чтобы найти скрытые ребра исходного графа.
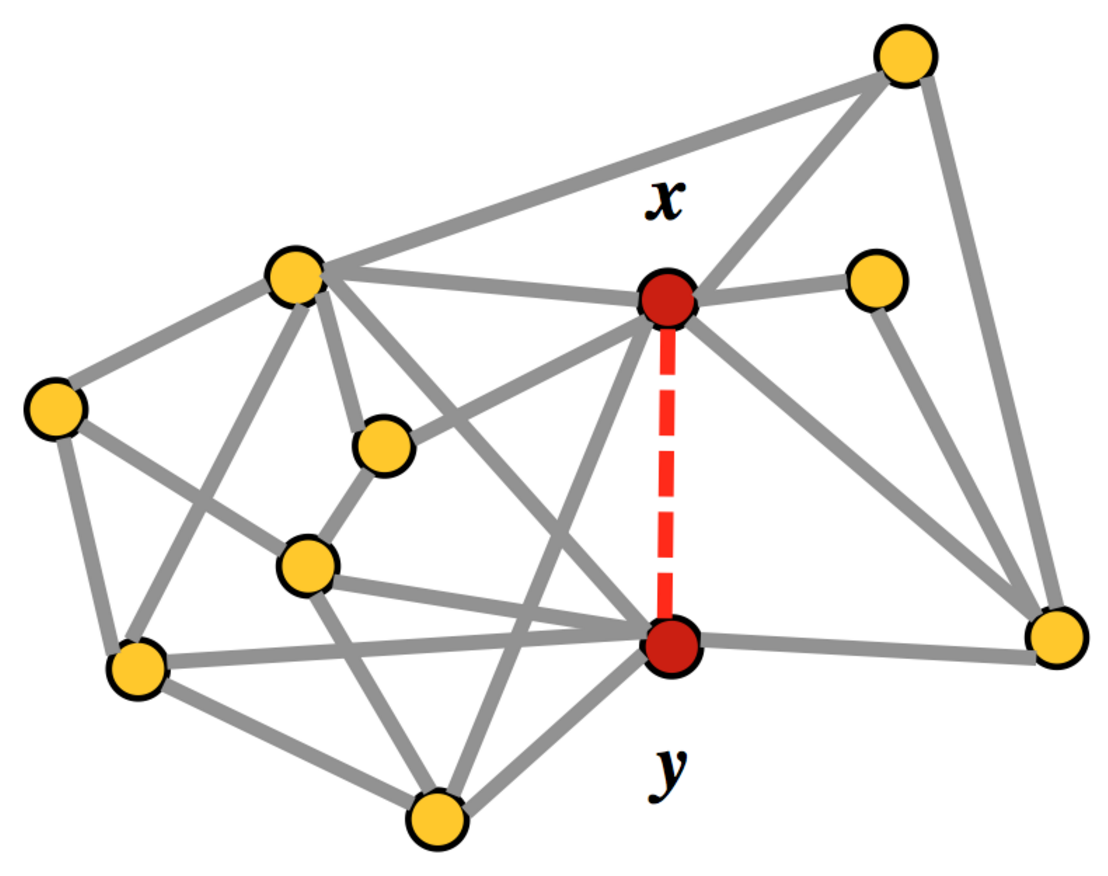
Помимо наличия связи между пользователями социальной сети, для каждой пары также была предоставлена информация о компаниях, в которых работают пользователи, информация о количестве отправленных и полученных сообщений, продолжительности звонков и количестве документы отправлены и получены.
Задача поиска ребер сформулирована как задача бинарной классификации, а мера предложена в качестве приемочной метрики.
Ф1 .
В некоторых подобных задачах метрика качества рассчитывается отдельно для каждого пользователя и оценивается среднее значение.
В этой задаче качество оценивалось глобально для всех ребер.
Обучение и тестирование
В общем случае для поиска скрытых ребер в графе необходимо перебрать все возможные пары вершин и для каждой пары получить оценку вероятности соединения.Для больших графов такой подход потребует много вычислительных ресурсов.
Поэтому на практике набор кандидатов в социальные графы ограничивается только парами, имеющими хотя бы одного общего друга.
Как правило, такое ограничение позволяет существенно сократить объем вычислений и ускорить работу алгоритма без существенной потери качества.
Каждая пара кандидатов описывается вектором признаков и двоичным ответом: «1», если ребро есть, или «0», если ребро отсутствует. С помощью полученного набора {вектор признаков, ответ} обучается модель, прогнозирующая вероятность наличия ребра для пары кандидатов.
Т.
к.
граф в этой задаче неориентированный, то вектор признаков не должен зависеть от перестановки кандидатов в паре.
Это свойство позволяет учитывать пару кандидатов только один раз за время обучения и уменьшить размер обучающей выборки вдвое.
Чтобы ответить на вопрос, какие ребра скрыты в исходном графе, оценку вероятности на выходе модели необходимо преобразовать в двоичный ответ, выбрав соответствующее пороговое значение.
Для оценки качества и выбора параметров модели мы удалили из предоставленного графа 5% случайно выбранных ребер.
Оставшийся граф использовался для поиска кандидатов, генерации признаков и обучения модели.
Скрытые края использовались для выбора порога и итоговой оценки качества.
Основные подходы к генерации признаков в задаче PYMK описаны ниже.
Счетчики
Для каждого пользователя мы рассчитываем статистику: распределение друзей по географии, сообществу, возрасту или полу.Используя эту статистику, мы получаем оценку сходства кандидатов друг с другом, например, с помощью скалярного произведения.
Сходство наборов и общие друзья
Коэффициент Жаккард — позволяет оценить сходство двух наборов.Наборами могут быть как друзья, так и, например, сообщества кандидатов.
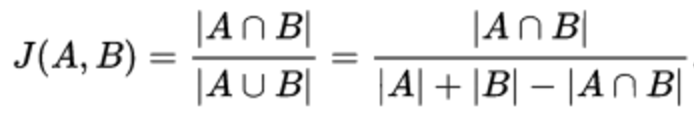
Коэффициент Адамик/Адара — по сути, взвешенная сумма общих друзей двух кандидатов.
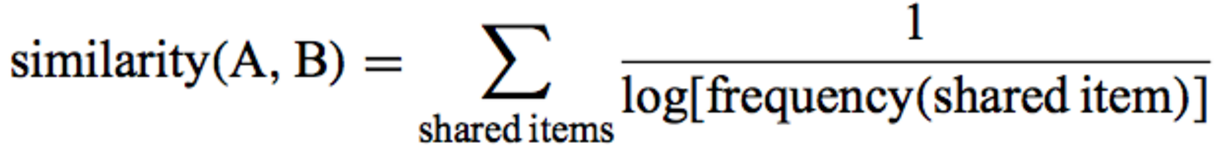
Вес в этой сумме зависит от количества друзей общего друга.
Чем меньше друзей у общего друга, тем больший вклад он вносит в полученную сумму.
Кстати, эту идею мы активно использовали в нашем решении.
Скрытые факторы
Эти признаки получаются в результате матричных разложений.Более того, декомпозицию можно применять как к матрице связей между пользователями, так и к матрицам сообщество-пользователь, география-пользователь и тому подобное.
Векторы со скрытыми признаками, полученные в результате декомпозиции, можно использовать для оценки сходства объектов друг с другом, например, с помощью косинусная мера расстояния.
Пожалуй, наиболее распространенным алгоритмом разложения матрицы является СВД .
Вы также можете использовать популярный алгоритм в рекомендательных системах.
Л.
С.
и алгоритм поиска сообществ в графах БольшойКЛАМ .
Знаки на графиках
Эта группа признаков рассчитывается с учетом структуры графа.Как правило, для экономии времени в расчетах используется не весь граф, а какая-то его часть, например, подграф общих друзей глубины 2. Одной из популярных примет является Время удара — среднее количество шагов, необходимое для прохождения маршрута от одного кандидата к другому с учетом весов ребер.
Путь проложен таким образом, что следующая вершина выбирается случайным образом с вероятностью, зависящей от значений атрибутов ребер, исходящих из текущего узла.
Решение
При решении этой задачи мы активно использовали заложенную в коэффициенте Адамика/Адара идею о том, что не все друзья одинаково полезны.Мы экспериментировали с функцией дисконтирования — пробовали дробные степени вместо логарифмов — а также экспериментировали с взвешиванием общих друзей по различным атрибутам полезности.
Т.
к.
над задачей мы работали параллельно, то в итоге у нас получилось два независимых решения, которые в дальнейшем были объединены для итоговой подачи.
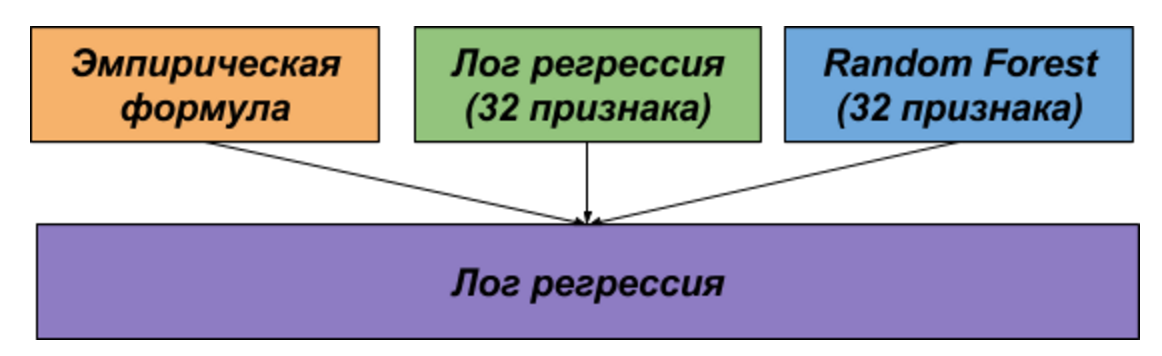
Первое решение основано на идее Адамика/Адара и представляет собой эмпирическую формулу, учитывающую как количество друзей общего друга, так и поток сообщений между кандидатами через общих друзей.
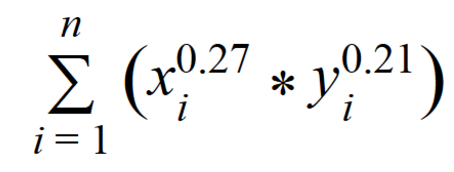
n — количество общих друзей;
xi — количество друзей у общего друга;
yi — сумма входящих и исходящих сообщений между кандидатами через их общего друга.
Во втором решении мы сгенерировали 32 функции и обучили на них модель журнала.
регрессия и случайный лес.
Модели первого и второго решения были объединены с использованием другой логистической регрессии.
В таблице описаны основные возможности, которые использовались во втором решении.
| знак | описание |
|---|---|
| взвешенный_commom | Аналог коэффициента Адамика/Адары, но вместо логарифма использован корень третьей степени |
| проводимость_общий | Взвешиваем общих друзей с учетом проводимости сообщений.
Чем меньше соотношение исходящих и входящих сообщений/звонков/документов общего друга, тем выше его вес при суммировании |
| flow_common | Оцениваем поток сообщений/звонков/документов между кандидатами через общего друга.
Чем выше проходимость, тем больше вес в сумме |
| друзья_жаккард | Коэффициент Жаккара для друзей кандидатов |
| друг_компания | Сходство на основе доли друзей пользователя из компании кандидата |
| компания_жаккард | Дружелюбие компаний-кандидатов оцениваем с помощью коэффициента Жаккара (равен единице, если кандидаты из одной компании) |
В таблице ниже приведены оценки качества как отдельно, так и по полученным моделям.
| Модель | Ф1 | Точность | Полнота |
|---|---|---|---|
| Ээмпирическая формула | 0.064 | 0.059 | 0.069 |
| Журнал регрессии | 0.060 | 0.057 | 0.065 |
| Случайный лес | 0.065 | 0.070 | 0.062 |
| Лог-регрессия + случайный лес | 0.066 | 0.070 | 0.063 |
| Логарифмическая регрессия + случайный лес + эмпирическая формула | 0.067 | 0.063 | 0.071 |
Выбор порога
Итак, модель обучена.Следующим шагом является выбор порога для оптимизации показателя приемлемости.
В этой задаче мы оптимизировали метрику Ф1 .
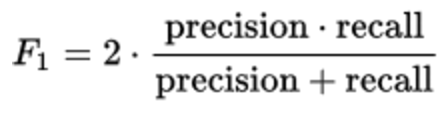
Эта метрика одинаково чувствительна как к точности, так и к полноте и представляет собой среднее гармоническое этих величин.
Поскольку зависимость метрики F1 от порога является выпуклой функцией, то найти максимум не составит труда.
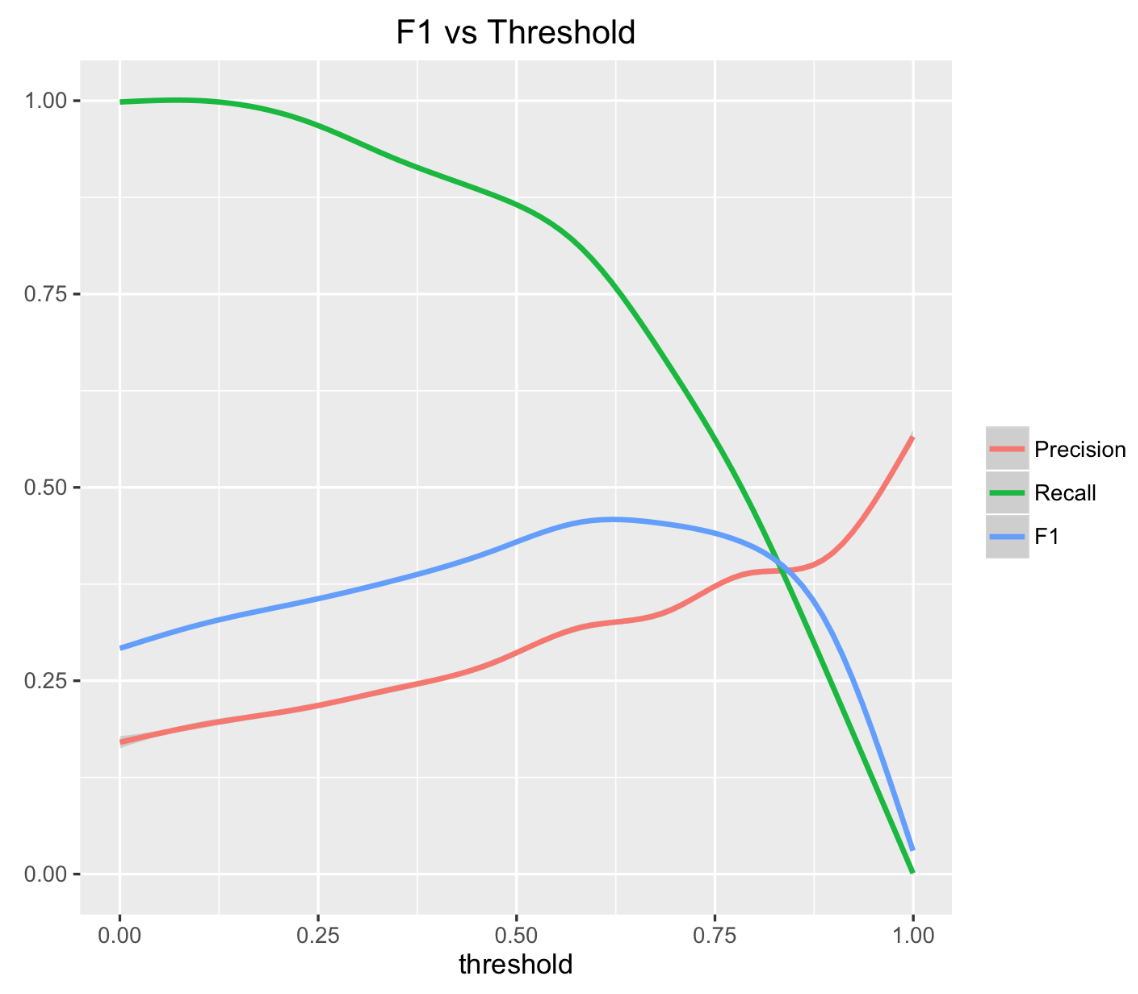
В этой задаче мы использовали алгоритм двоичного поиска для выбора оптимального порогового значения.
Технологии
Исходный граф был задан как список ребер с указанием идентификаторов пользователей и соответствующих атрибутов.Всего в обучающей выборке было представлено 5,5 млн соединений.
Исходные данные предоставляются в виде текстового файла в формате csv и занимают на жестком диске 163 МБ.
В рамках хакатона нам были предоставлены ресурсы облачного сервиса Azure по программе Microsoft БизСпарк , в котором мы создали виртуальную машину для наших вычислений.
Стоимость сервера в час составляла 0,2$ и не зависела от интенсивности вычислений.
Бюджета, выделенного организаторами, хватило для решения этой проблемы.
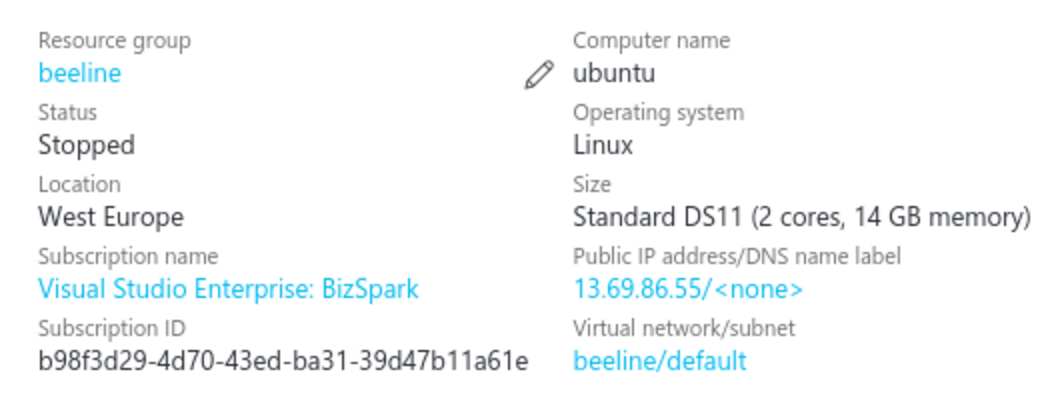
Мы реализовали алгоритм поиска общих друзей на Spark; результаты промежуточных вычислений кэшировались на диске в паркетном формате, что позволяло существенно сократить время чтения данных.
Время работы алгоритма поиска общих друзей на виртуальной машине составило 8 часов.
Кандидаты со списком общих друзей в паркетном формате занимают 2,1Гб.
Алгоритм обучения и выбора параметров модели реализован на Python с помощью пакета scikit-learn .
Процессы генерации признаков, обучения модели и выбора порога на виртуальном сервере в общей сложности заняли около 3 часов.
В заключение я хотел бы поблагодарить Брагина Ивана за активное участие в решении задачи и творческий подход к выбору эмпирической формулы.
Теги: #Машинное обучение #социальный граф #рекомендации #Data Mining #хакатон #Data Mining

-
Паранойя
19 Oct, 24 -
Программирование Под Дулом Пистолета
19 Oct, 24 -
Схема Шнорра И Ее Роль В Биткойне
19 Oct, 24 -
Конференция Линканбан 2015
19 Oct, 24 -
Нужен Ли Хабраголик Для Windows/Unix?
19 Oct, 24


