В какой-то момент во время разработки игры я столкнулся с проблемой производительности на современных ПК.
У нашего моделлера есть довольно мощный современный компьютер красного цвета.
Но наш проект жутко тормозил, нагружая одно ядро процессора.
Причина проста — новые процессоры имеют много ядер, но по факту они менее производительны в однопоточных приложениях.
В то время у меня был однопоточный рендеринг.
Но на самом деле причина была не столько в этом.
И в процессе поиска проблемы я решил посчитать, сколько полигонов присутствует в сцене: 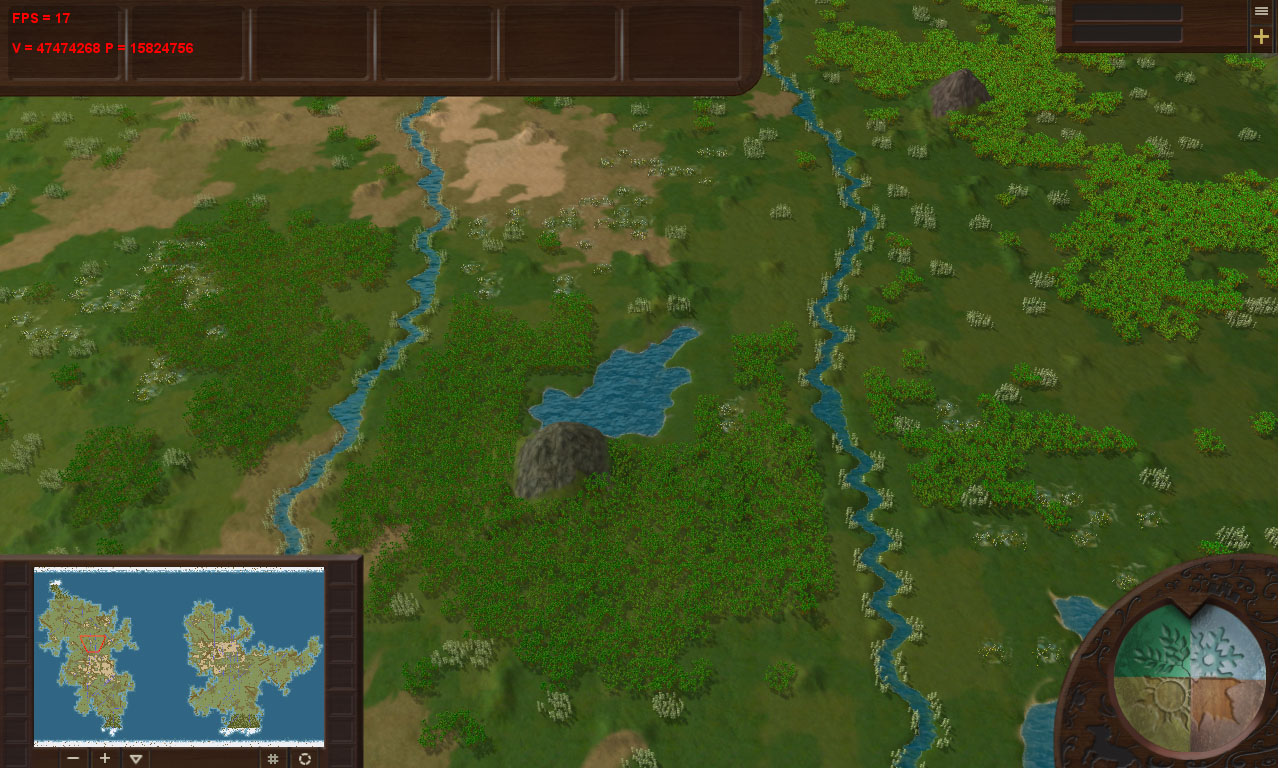
На средней игровой карте, на максимальном расстоянии и с большим скоплением пальм - 15 824 756 треугольников! Почти 16 миллионов! Огромное количество.
Немного поигравшись с генератором карт, мне удалось найти место с 16,75 миллионами: 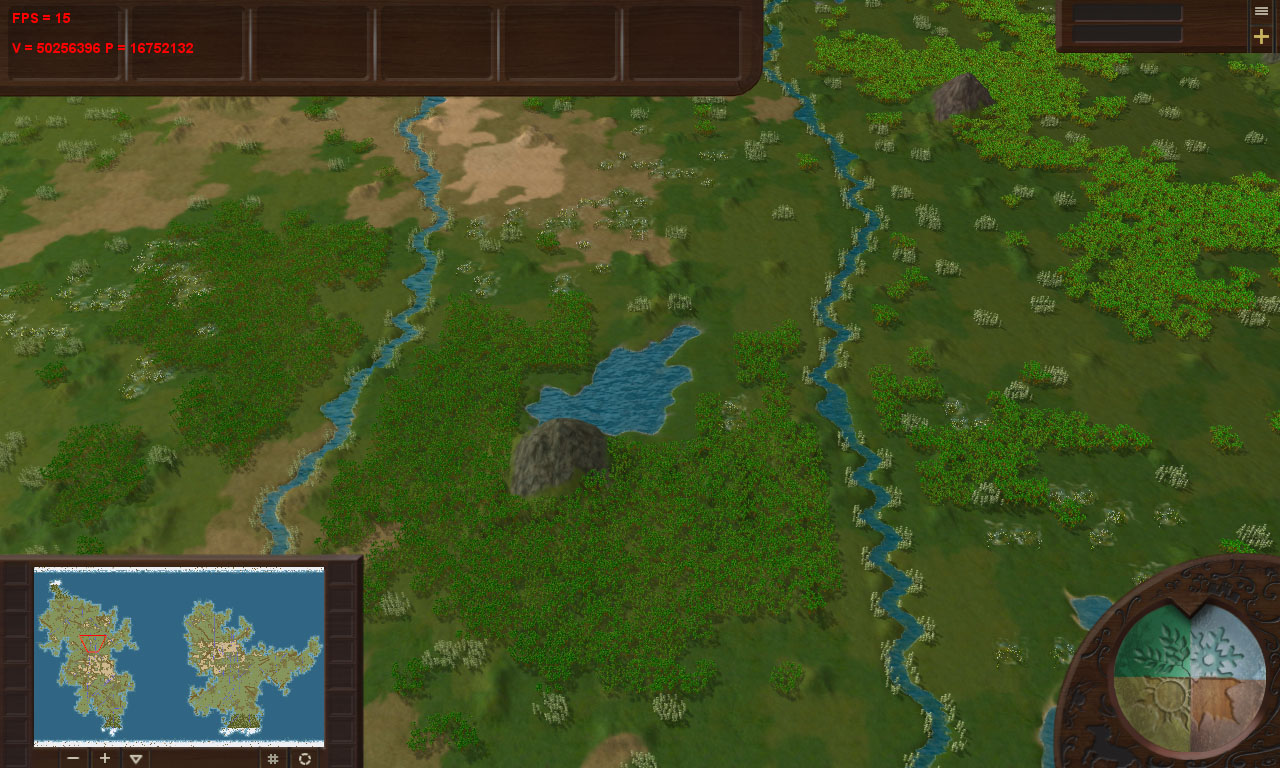
Хотя подобное место с елками дало всего 8,5 миллионов треугольников: 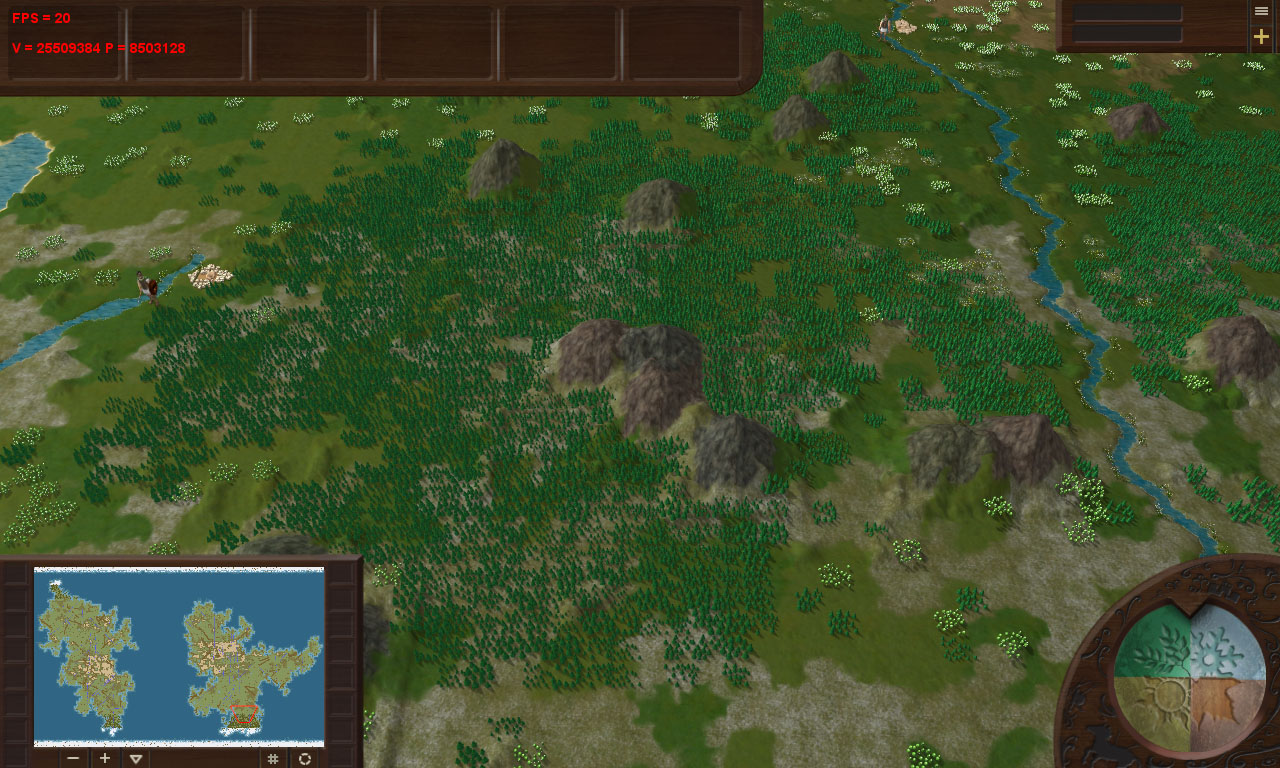
В среднем сцена состояла из ~4 миллионов: 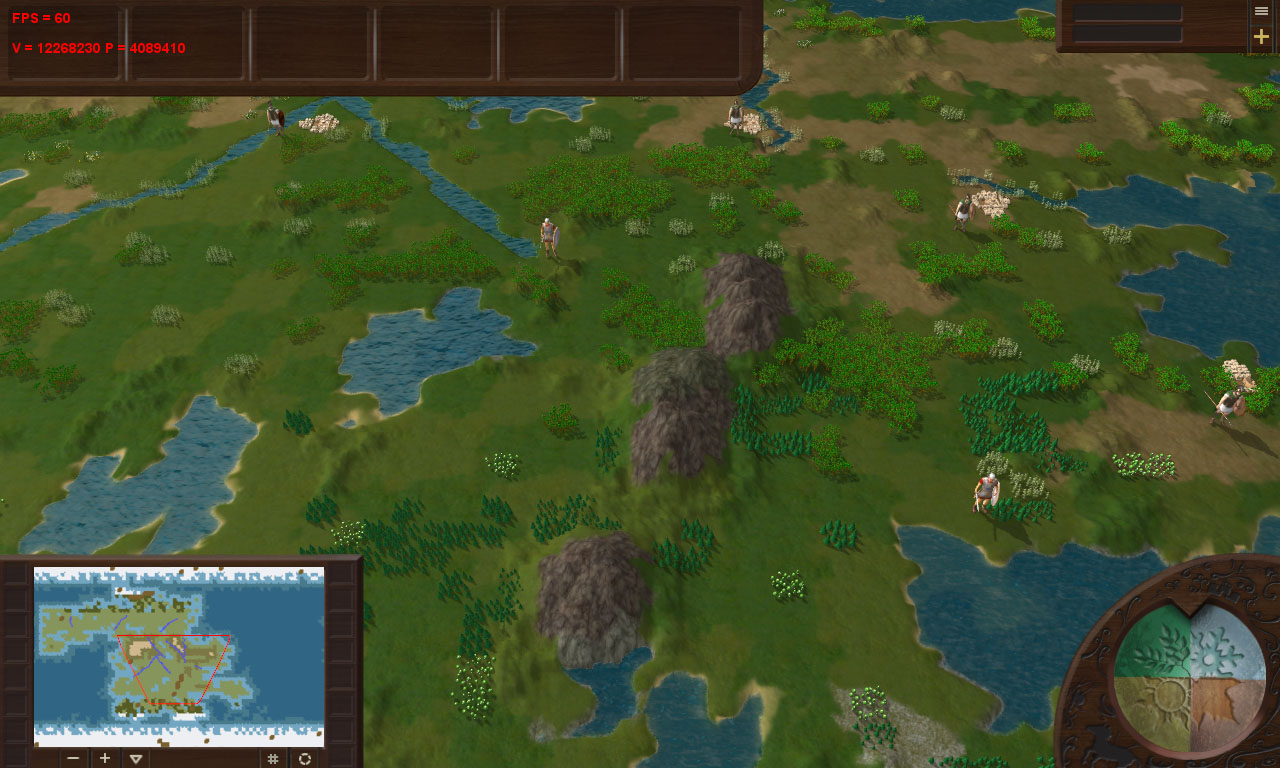
В целом я был рад, что мой рендер смог обработать такое огромное количество треугольников, но их количество было избыточным.
Решение было на поверхности:
- Оптимизируйте количество полигонов в моделях.
- Оптимизируйте полигональную сетку ландшафта.
- Реализация многопоточного рендеринга.
1. Оптимизация количества полигонов в моделях
В нашем движке растительность рисуется «пачками», весь ландшафт разбит на тайлы и субтайлы, минимальный пакет — один субтайл.

Один пакет — это одна сетка, поскольку уменьшение количества сеток значительно снижает количество вызовов CPU-> GPU. 
Изначально наши елочки состояли из усеченных шишек, но перейдя на полноценные шишки, нам удалось убрать пару лишних треугольников: 
Вишенкой на торте стало решение убрать стволы деревьев, так как с нашего ракурса их просто не было видно.
В результате нам удалось сократить количество полигонов на одной упаковке елок в среднем на 40%.
Различия практически незаметны: 
С пальмами было сложнее, но паки по 5000 - 6000 полигонов нужно было подправить.
Как добиться массивности и густоты джунглей? Высокая густота джунглей достигнута за счет большого количества пальм: 
Мы решили упростить пальмы и ввести второй слой растительности, что позволило сохранить видимую плотность и добиться желаемых 600 – 700 полигонов в паке.

Уменьшение количества полигонов в 10 раз — отличный результат. 
2. Оптимизация полигональной сетки ландшафта.
Изначально сетка ландшафта выглядела так: 
На скриншоте показаны ровные участки ландшафта, это тайлы лугов, равнин и даже других ровных поверхностей.
Я решил убрать некоторые мелкие неровности ландшафта.
Тем самым увеличивая площадь плиток равной высоты.
Просто проверив все вершины тайлов и субтайлов на одинаковую высоту, мне удалось добиться следующего результата: 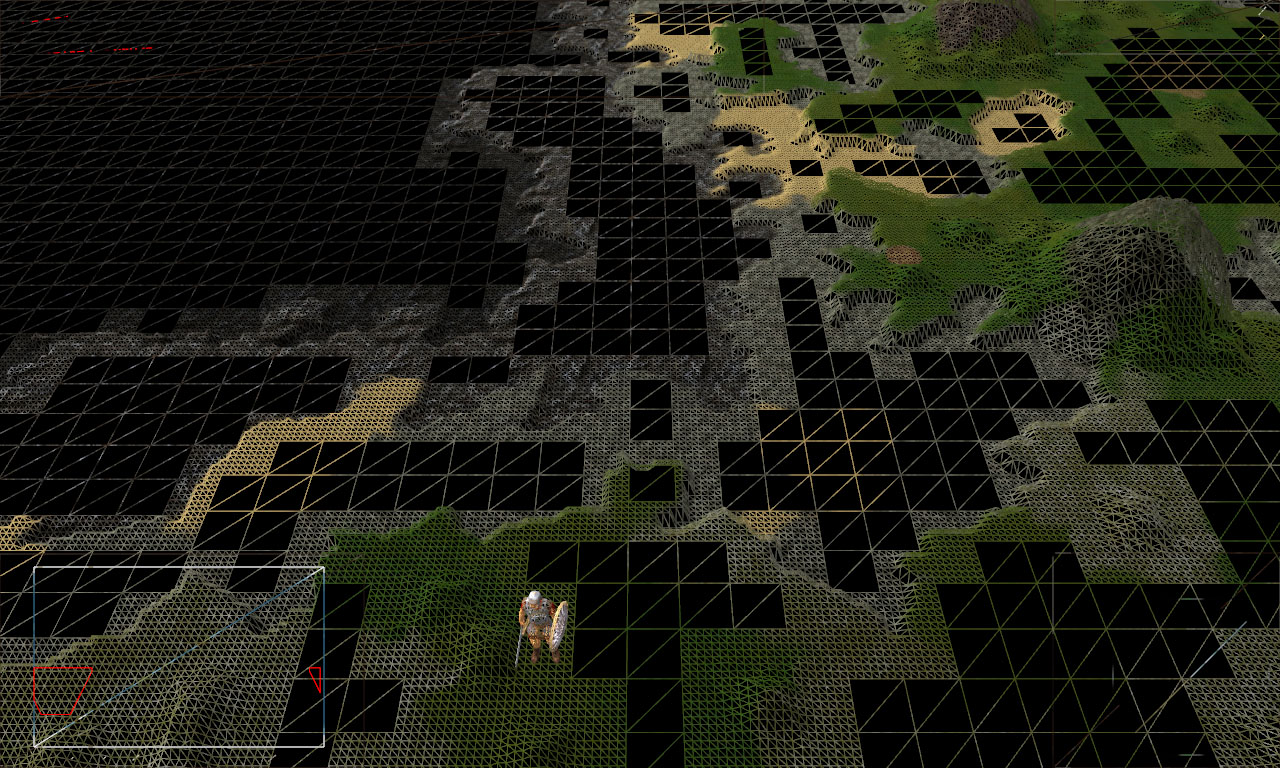
Остались еще ровные места, которые можно было оптимизировать, и я начал строить полигоны из тех треугольников, которые имели одинаковую высоту.
Была взята плитка и все ее треугольники рассортированы на массив треугольников неравной высоты и на список массивов, состоящий из треугольников одинаковой высоты и соседних треугольников.

В приведенном примере результатом было: 1 массив треугольников, которые нельзя было изменить, так как все они были разной высоты (красные треугольники) и список, состоящий из двух массивов треугольников одинаковой высоты (массивы заполнены цветом ).
Теперь стояла задача найти из массива треугольников их выпукло-вогнутый контур (Concave Hull), причем многие треугольники могли иметь дырки.
Раньше в своей работе я сталкивался с выпуклыми контурами (Convex Hull), проблем с ними не было, я уже использовал алгоритм Грэма (сканирование Грэма).
Но с постройкой Concave Hull возникли проблемы.
Найти информацию на эту тему в Интернете оказалось довольно сложно.
Пришлось писать реализацию алгоритмов с нуля.
Не совру, если скажу, что прочитал десяток разных диссертаций на эту тему.
Но все предложенные алгоритмы давали приблизительный результат с некоторой погрешностью.
После недели мучений и боли у меня возникла идея собственного алгоритма.
Я попробовал построить контур, используя множество вершин треугольников, т. е.
преобразовал массив треугольников в массив вершин и использовал их для построения оболочки.
Но для моей задачи этого не требовалось.
По моим выводам, снаряд было проще построить непосредственно из треугольников, а точность вогнутого корпуса составила 100%.
Изначально я хотел выложить сюда портянку исходного кода алгоритма, но мне кажется проще описать его в двух словах: В основе лежит правило: если вершина треугольника входит в четыре и меньше треугольников, тогда одно из ребер, образуемых вершиной, лежит на границе.
Далее формируется список таких ребер с учетом удаления одинаковых ребер.
Находим ребро с наименьшими X и Y и оттуда начинаем проход/сортировку ребер, попутно добавляя в список уникальные вершины.
Этот список будет оболочкой набора треугольников.
Единственное, что в итоге, — это удалить из полученного списка коллинеарные точки.
В результате я мог построить Вогнутый Корпус практически любой сложности.
Этот алгоритм не подходил для набора с дырками, но я обошел это, просто разделив этот набор на две половины вдоль отверстия.
Далее я получил контур и триангулировал его: 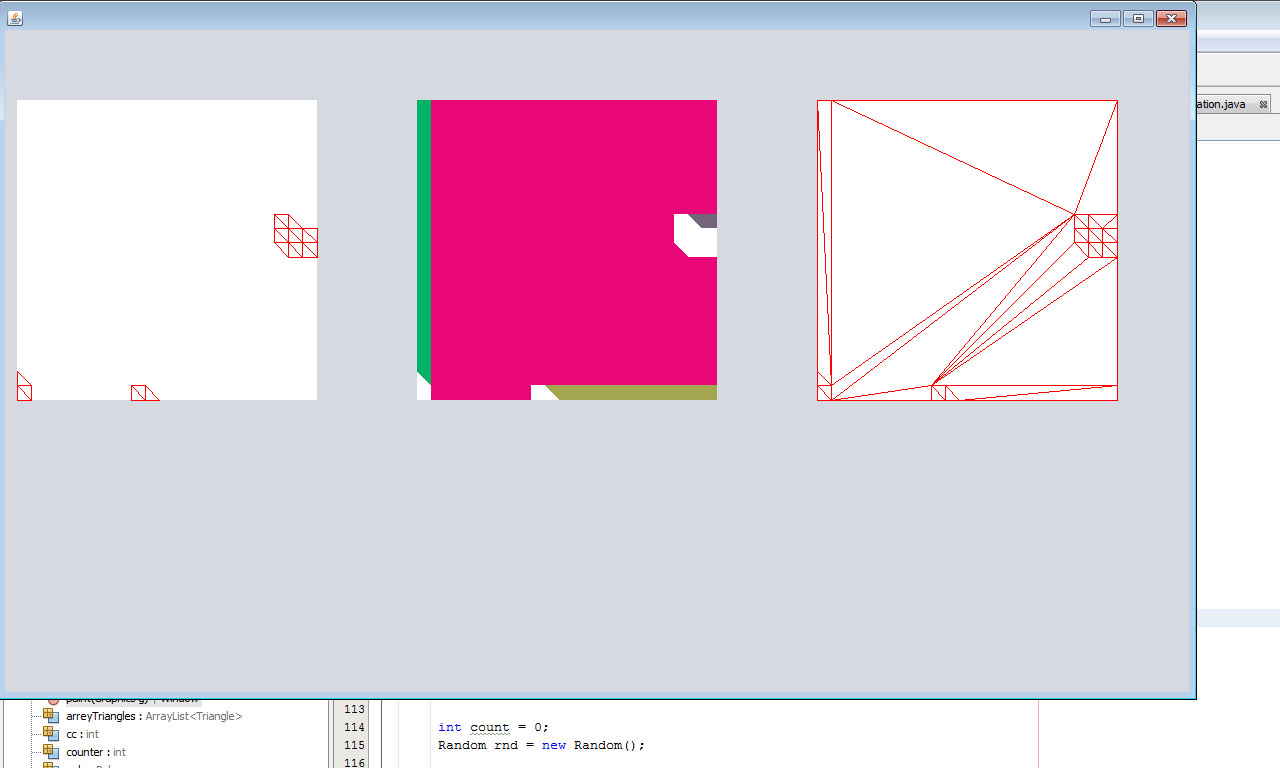
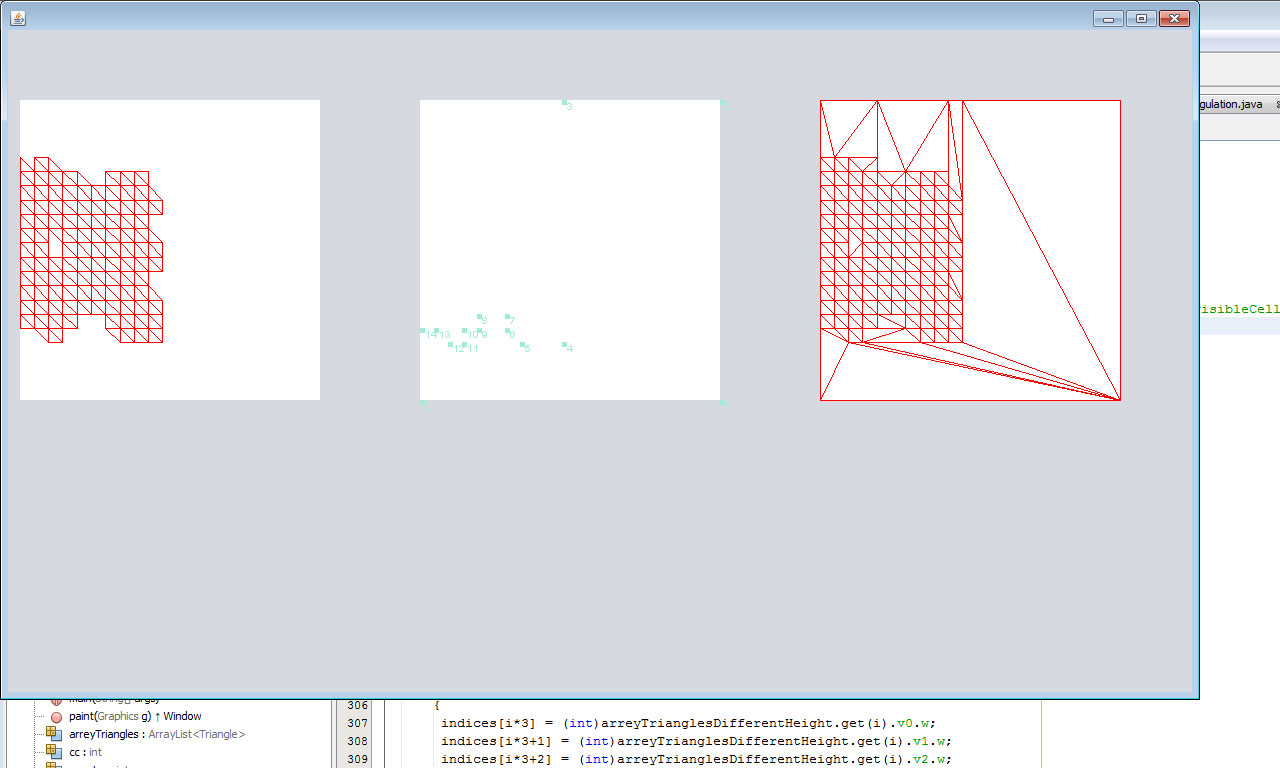
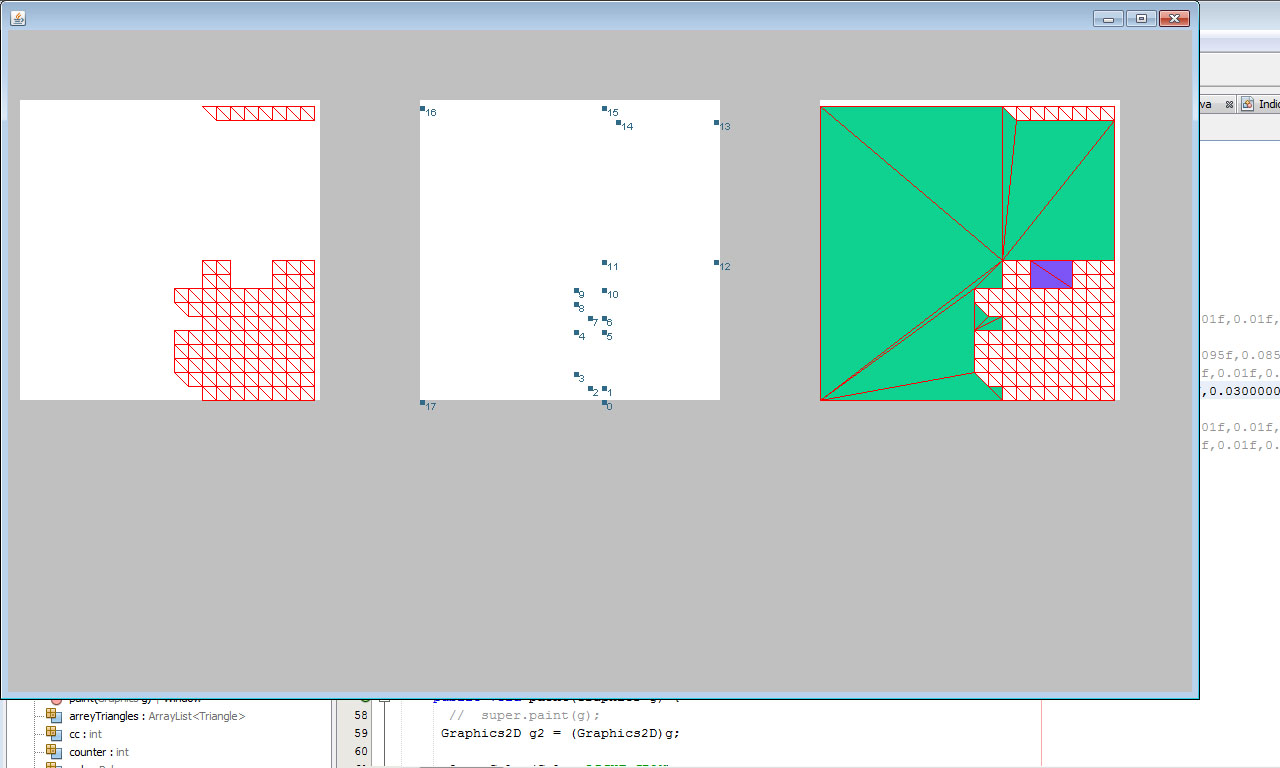
Все получилось великолепно: 
Но в итоге я был расстроен результатом.
Разработанный мною алгоритм дал заметный прирост производительности при рендеринге сцены, так как количество полигонов сократилось в среднем на 60 – 70%.
Но при этом генерация карт стала происходить в 10 раз медленнее.
Алгоритм оказался очень трудоемким.
На продумывание облегченной версии алгоритма оптимизации полигональной сетки ландшафта ушло три дня, что дало следующие результаты: 
Теперь расчеты данных для оптимизации стали незаметны на фоне генерации карт, а количество полигонов уменьшилось в среднем на 40-50%.
Данная статья носит предварительный и поверхностный характер.
Если кому-то интересна тема разработки игр, я готов продолжить и дополнить статью конкретными шагами, решениями и планами на будущее.
Также, думаю, вас заинтересует тема построения многопоточного приложения Open GL, разработанного на Java, о которой я постараюсь рассказать в следующей статье.
Теги: #Разработка игр #Алгоритмы #java #open gl #Вогнутый корпус

-
Ноутбук Sony Vaio Vpceb1J1E/Wi
19 Oct, 24 -
Тонеры От А До Я
19 Oct, 24 -
Как Мы Гасили Байку Техподдержки
19 Oct, 24 -
Телефон Мечты
19 Oct, 24 -
Где Трамвай? И Вот Где
19 Oct, 24 -
Askozia - Редактор Маршрутов Вызовов
19 Oct, 24


