Обучение С Подкреплением Для Самых Маленьких

Награда представлена как величина изменения расстояния от стены до тележки во время движения.

Расстояние D от стены измеряется дальномером.

Перемещение в данном примере возможно только при определенном смещении «привода», состоящего из двух стрел S1 и S2. Стрелы представляют собой два сервопривода с направляющими, соединенными в виде «локтя».

Каждый сервопривод в этом примере может вращаться на 6 равных углов.

Модель имеет возможность выполнять 4 действия, которые представляют собой управление двумя сервоприводами, действия 0 и 1 поворачивают первый сервопривод на определенный угол по часовой стрелке и против часовой стрелки, действия 2 и 3 поворачивают второй сервопривод на определенный угол по часовой стрелке и против часовой стрелки.

На рисунке 1 показан рабочий прототип тележки.

Рис.

1. Прототип тележки для экспериментов по машинному обучению На рисунке 2 стрела S2 выделена красным, стрела S1 — синим, а 2 сервопривода — черным.

Рис.

2. Система двигателя Схема системы представлена на рисунке 3. Расстояние до стены обозначено буквой D, дальномер показан желтым цветом, привод системы выделен красным и черным цветом.

Рис.

3. Схема системы Диапазон возможных положений S1 и S2 показан на рисунке 4:



Рис.

4.а.

Диапазон положения стрелы S1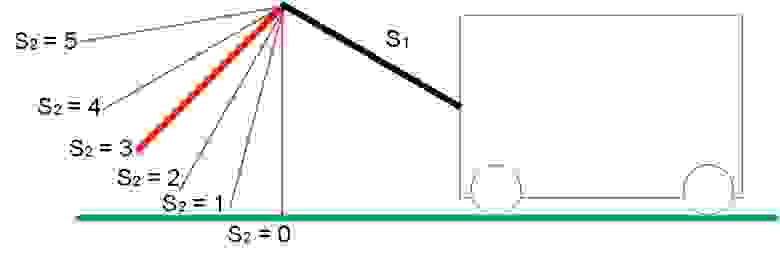



Рис.

4.б.

Диапазон положения стрелы S2 Предельные положения привода показаны на рисунке 5: При S1=S2=5 максимальное расстояние от земли.

Когда S1 = S2 = 0, минимальное расстояние до земли.

Рис.

5. Граничные положения стрел S1 и S2. «Привод» имеет 4 степени свободы.

Действие меняет положение стрелок S1 и S2 в пространстве по определенному принципу.

Типы действий показаны на рисунке 6.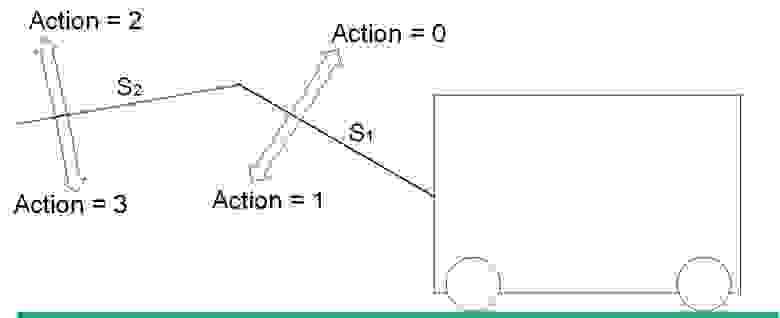



Рис.

В нашем примере награда равна 1.



Рис.

7. Системное движение с положительным вознаграждением В положении S1 = 0, S2 = 0 действие 2 перемещает тележку к стене, система получает отрицательное вознаграждение, равное изменению расстояния до стены.

В нашем примере награда равна -1.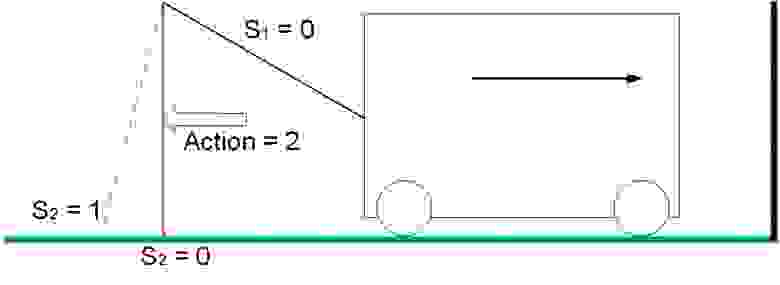



Рис.

8. Движение системы с отрицательным вознаграждением В остальных состояниях и любых действиях «диска» система будет стоять на месте и награда будет равна 0. Хотелось бы отметить, что устойчивым динамическим состоянием системы будет последовательность действий 0-2-1-3 из состояния S1=S2=0, при которой тележка будет двигаться в положительном направлении с минимальным количеством потраченные действия.

Колено поднято – колено выпрямлено – колено опущено – колено согнуто = тележка двинулась вперед, повторите.

Таким образом, с помощью метода машинного обучения необходимо найти такое состояние системы, такую конкретную последовательность действий, награда за которую не будет получена сразу (действия 0-2-1 – награда за которую равна 0 , но которые нужны для получения 1 для последующего действия 3 ).

Матрица Q представляет собой совокупность всех возможных состояний системы и весов реакции системы на различные действия.

В этой задаче возможные комбинации параметров системы составляют 36 = 6^2. В каждом из 36 состояний системы можно совершить 4 разных действия (Действие = 0,1,2,3).

На рисунке 9 показано исходное состояние матрицы Q. Нулевой столбец содержит индекс строки, первая строка содержит значение S1, вторая – значение S2, последние 4 столбца равны весам для действий, равным 0, 1. , 2 и 3. Каждая строка представляет уникальное состояние системы.

При инициализации таблицы все значения весов приравниваем к 10.



Рис.

9. Инициализация матрицы Q После обучения модели (~15000 итераций) матрица Q имеет вид, показанный на рисунке 10.



Рис.

10. Матрица Q после 15 000 итераций обучения.

Обратите внимание, что действия с весами, равными 10, в системе невозможны, поэтому значение весов не изменилось.

Например, в крайнем положении с S1=S2=0 действия 1 и 3 выполнить невозможно, так как это ограничение физической среды.

Эти граничные действия запрещены в нашей модели, поэтому алгоритм не использует 10. Рассмотрим результат работы алгоритма: … Итерация: 14991, было: S1=0 S2=0, действие= 0, сейчас: S1=1 S2=0, приз: 0 Итерация: 14992, было: S1=1 S2=0, действие= 2, сейчас: S1=1 S2=1, приз: 0 Итерация: 14993, было: S1=1 S2=1, действие= 1, сейчас: S1=0 S2=1, приз: 0 Итерация: 14994, было: S1=0 S2=1, действие= 3, сейчас: S1=0 S2=0, приз: 1 Итерация: 14995, было: S1=0 S2=0, действие= 0, сейчас: S1=1 S2=0, приз: 0 Итерация: 14996, было: S1=1 S2=0, действие= 2, сейчас: S1=1 S2=1, приз: 0 Итерация: 14997, было: S1=1 S2=1, действие= 1, сейчас: S1=0 S2=1, приз: 0 Итерация: 14998, было: S1=0 S2=1, действие= 3, сейчас: S1=0 S2=0, приз: 1 Итерация: 14999, было: S1=0 S2=0, действие= 0, сейчас: S1=1 S2=0, приз: 0 Давайте посмотрим поближе: Возьмем итерацию 14991 как текущее состояние.

1. Текущее состояние системы S1=S2=0, этому состоянию соответствует строка с индексом 0. Наибольшее значение - 0,617 (значения равные 10, описанные выше, игнорируем), оно соответствует Action = 0 Это означает, что согласно матрице Q, когда состояние системы S1=S2=0, мы выполняем действие 0. Действие 0 увеличивает значение угла поворота сервопривода S1 (S1 = 1).

2. Следующему состоянию S1=1, S2=0 соответствует строка с индексом 6. Максимальное значение веса соответствует Action = 2. Выполняем действие 2 – увеличиваем S2 (S2 = 1).

3. Следующему состоянию S1=1, S2=1 соответствует строка с индексом 7. Максимальное значение веса соответствует Action = 1. Выполняем действие 1 – уменьшаем S1 (S1 = 0).

4. Следующему состоянию S1=0, S2=1 соответствует строка с индексом 1. Максимальное значение веса соответствует Action = 3. Выполняем действие 3 – уменьшаем S2 (S2 = 0).

5. В результате мы вернулись в состояние S1=S2=0 и заработали 1 призовой балл.

На рисунке 11 показан принцип выбора оптимального действия.

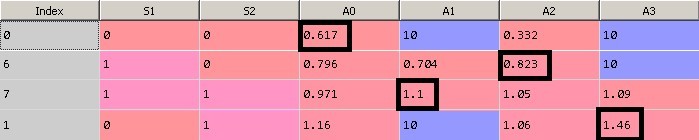
Рис.

11.а.

Матрица Q



Рис.

11.б.

Матрица Q Давайте подробнее рассмотрим процесс обучения.

Установите исходное положение колена в самое верхнее положение:

s1=s2=5.

Мы инициализируем матрицу Q, заполняя ее начальным значением:

initializeQ();

Давайте посчитаем параметр эпсилон .

Это вес «случайности» действия алгоритма в нашем расчете.

Чем больше итераций обучения прошло, тем меньше случайных значений действия будет выбрано:

epsilon = math.exp(-float(t)/explorationConst)

Для первой итерации:

epsilon = 0.996672

Сохраним текущее состояние:

s01 = s1; s02 = s2

Давайте получим «лучшее» значение действия:

current_action = getAction();

Давайте подробнее рассмотрим функцию.

Функция getAction() возвращает значение действия, соответствующее максимальному весу с учетом текущего состояния системы.

Берется текущее состояние системы в матрице Q и выбирается действие, имеющее максимальный вес.

Обратите внимание, что данная функция реализует механизм случайного выбора действий.

С увеличением количества итераций случайный выбор действия уменьшается.

Это сделано для того, чтобы алгоритм не застревал на первых найденных вариантах и мог пойти по другому пути, который может оказаться лучше.

В начальном положении стрелок возможны только два действия: 1 и 3. Алгоритм выбрал действие 1. Далее определяем номер строки в матрице Q для следующего состояния системы, в которое система перейдет после выполнения действия, полученного нами на предыдущем шаге.

setSPrime(current_action);

В реальной физической среде после выполнения действия мы получили бы вознаграждение, если бы за ним последовало движение, но поскольку движение тележки моделируется, необходимо ввести вспомогательные функции для имитации реакции физической среды на действия.

(setPhysicalState и getDeltaDistanceRolled()) Выполним функции:

setPhysicalState(current_action);

— моделируем реакцию окружающей среды на выбранное нами действие.

Меняем положение сервоприводов и перемещаем тележку.

r = getDeltaDistanceRolled();

— Рассчитаем награду — расстояние, пройденное тележкой.

После выполнения действия нам необходимо обновить коэффициент этого действия в матрице Q для соответствующего состояния системы.

Логично, что если действие привело к положительному вознаграждению, то коэффициент в нашем алгоритме должен уменьшиться на меньшую величину, чем при отрицательном вознаграждении.

Теперь самое интересное: чтобы посчитать вес текущего шага, заглянем в будущее.

При определении оптимального действия, которое необходимо выполнить в текущем состоянии, мы выбираем наибольший вес в матрице Q. Поскольку мы знаем новое состояние системы, в которое мы перешли, мы можем найти максимальное значение веса из таблицы Q для этого состояния:

lookAheadValue = getLookAhead();

В самом начале он равен 10. И для расчета текущего веса мы используем значение веса еще не выполненного действия.

sample = r + gamma*lookAheadValue; sample = 7.5 Q.iloc[s, current_action] = Q.iloc[s, current_action] + alpha*(sample - Q.iloc[s, current_action] ) ; Q.iloc[s, current_action] = 9.75

Те.

мы использовали значение веса следующего шага для расчета веса текущего шага.

Чем больше вес следующего шага, тем меньше мы будем уменьшать вес текущего шага (по формуле) и тем предпочтительнее будет текущий шаг в следующий раз.

Этот простой прием дает хорошие результаты сходимости алгоритма.

Довольно быстро Q-матрица займет всю оперативную память.

Ниже приведен пример кода для построения сводной матрицы состояний и весов модели.

При количестве «стрелок» s_features = 5 и количестве различных положений стрелок s_states = 10 матрица Q имеет размерности (100000, 9).