Зачем нужен этот пост? Идея этого поста — кратко и понятно объяснить, как эти алгоритмы работают на графах.
То есть цель поста — в первую очередь понимание, а не детали реализации в коде.
Зачем нужны эти алгоритмы?
Обход в ширину и обход в глубину — это два алгоритма, которые составляют основу для наиболее сложных алгоритмов, имеющих реальные приложения.Не задумываясь, мы постоянно сталкиваемся с графиками.
Как самый банальный пример — навигатор.
Построение маршрута — это уже задача, в которой используются эти алгоритмы.
Поиск в глубину (DFS)
Один из основных методов обхода графа, часто используемый для проверки связности графа, поиска циклов и сильно связных компонент, а также для топологической сортировки.Давайте пока отбросим все эти сложные слова, а пока давайте посмотрим, что и как делает DFS. Мы будем считать реализацию списка смежности наиболее простой для понимания.
Кратко напомню, что список смежности — это один из способов представления графа, который выглядит примерно так: 
список смежности для данного графа Для каждой вершины (первого столбца) составляем список смежных с ней вершин, то есть список вершин, с которыми эта имеет общие ребра (ребро, инцидентное этим вершинам).
Теперь к самому алгоритму, принцип его работы совпадает с его названием, этот алгоритм идет «внутри» графа до тех пор, пока ему некуда идти, затем возвращается в предыдущую вершину и снова идет из нее до тех пор, пока не будет куда идти.
И так далее.
Для понимания этого алгоритма нам понадобятся 3 цвета, один будет обозначать, что мы еще не побывали на вершине, второй, что мы побывали и ушли, и третий, что мы побывали и не смогли пройти дальше и начинаем возвращаться обратно.
.
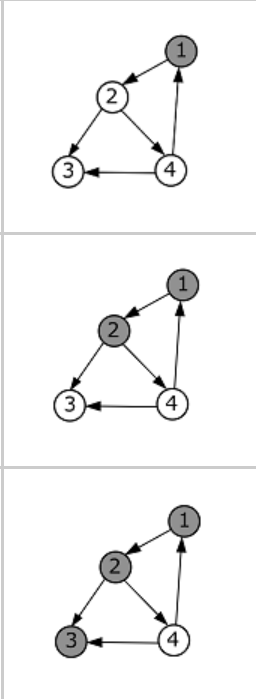
Первые 3 итерации.
Начинаем с любой вершины, например с первой.
Проходимся по списку смежности.
От 1 вершины добираемся до второй, переходим к ее списку смежности, не забываем 1 вершину закрасить серым, так как мы ее посетили и пошли дальше.
Из второй вершины переходим в любой из списка смежности второй вершины, например в 3. Закрашиваем 2 серым и переходим в список смежности 3-й вершины.
И ничего в нем нет. В этом случае мы понимаем, что дальше нам идти некуда, пора возвращаться.
Закрашиваем 3 черным, так как нам некуда идти (нет белых вершин, в которые можно было бы перейти из 3).
Возвращаемся к 2 и ее списку смежности, видим, что там еще есть вершина 4, перемещаемся туда, оттуда мы можем перейти только к 1, но она уже серая, то есть мы там уже были.
Алгоритм начнет рекурсивно откатываться, перекрашивая все вершины в черный цвет, принцип, думаю, уже понятен.

4, 5 и 6 итерации
Псевдокод

Что тут происходит? Все, что мы уже видели, находится только в коде.
G.Adj — список смежности этого графа.
Для каждой вершины, если она еще не посещена, мы окрашиваем ее в серый цвет, то есть ее посещенное поле устанавливается в значение true, таким образом мы пройдемся по всем вершинам.
Почему мы вызываем dfs для каждой вершины в init()? Мы можем не угадать с первой вершиной, как например на графике выше; если бы мы начали с вершины 3, то dfs сразу бы завершился, так как из нее нет исходящих дуг.
Поиск в ширину (BFS)
Систематически обходит все вершины графа.
Чем он отличается от обхода в глубину? Обход в глубину «перескакивает» между строками списка смежности по одной вершине за раз, а обход в ширину перескакивает через все возможные вершины сразу; посмотрим, как это работает на примере: 
БФС 
Сначала проходим по всем вершинам, смежным с начальной, затем по всем вершинам, смежным с исходной, и так далее.
Вот еще один пример, который, как мне кажется, более наглядно показывает разницу между обходами по глубине и ширине: в 1-м граф вроде бы пройден равномерно.
Псевдокод с краткими пояснениями: 
Заключение
Эти два алгоритма очень важно понимать.Я искренне надеюсь, что этот пост дал читателю хотя бы приблизительное представление о том, как работают обходы в глубину и в ширину, поскольку полное понимание вы получите только после применения этих алгоритмов на практике.
Теги: #Алгоритмы #алгоритм #граф #понимание #обход #сложныйпростой

-
Джанна Наннини Шведская Страница
19 Oct, 24 -
Секреты Тестирования Интерфейсов В Ткс Банке
19 Oct, 24 -
Гарри Поттер И Методы Рационального Мышления
19 Oct, 24 -
Краткая Инструкция По Работе С Клиентами
19 Oct, 24 -
Как Я Проходил Техсео.эксперт (1 Уровень)
19 Oct, 24 -
Неторати, Или Когда Блогеры Влюблены
19 Oct, 24 -
Израильтяне Изобрели Нано-Собаку
19 Oct, 24


