Нумерология В Ms Sql – Занимательный Эксперимент

Люди любили играть в числа с древних времен.

Докажите, что отношение длины пирамиды Хеопса к высоте равно.

не помню чему.

Физикам это тоже не чуждо, например есть Мистическая формула Койде , связывающий массы электрона, мюона и тау-частиц.

Есть формула постоянной тонкой структуры - в отличие от формулы Койде, она кажется очень искусственной.

Насколько верны такие формулы? Я провел эксперимент.

Нумерология в MS SQL – занимательный эксперимент

Возьмем N чисел: А, Б, С.

В своем эксперименте я ограничился тремя числами.

К каждому числу мы можем применить унарную функцию: SIN, COS, EXP, LN (я ограничился четырьмя).

Это дает 4*3=12 новых чисел, что вместе с исходными дает 15 чисел.

Далее применяем бинарные операции +, -, *, / к их комбинации.

(можно рассмотреть и другие, например, возведение в степень, но я опять же ограничился четырьмя).

Здесь 15*15*4 новых комбинаций (на самом деле меньше, так как некоторые операции запрещены, например, деление на 0, а для + и * количество комбинаций меньше из-за их симметричности).

Тогда мы сможем повторять эти шаги снова и снова.

Уже на втором шаге было 34 513 800 формул (теперь вы понимаете, почему я ограничил количество операций?), что дало мне целых 2 776 355 разных чисел для A=1, B=2, C =3. На графике выше показана концентрация (количество разных чисел) для длины 1 поддиапазона от -60 до +60. Шкала Y является логарифмической.

Видна концентрация цифр около 0.

Нумерология в MS SQL – занимательный эксперимент

Масштабируем диапазон -2.2: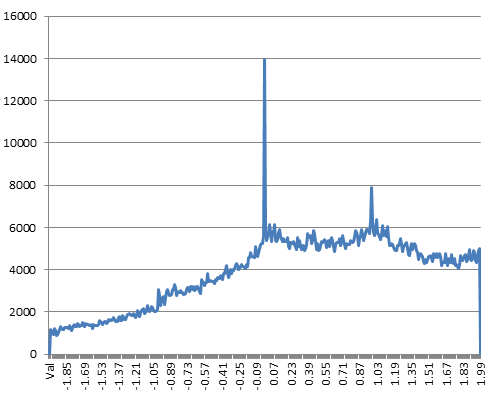

Здесь шкала Y уже нормальная.

Пики около 0 и 1. Максимально увеличиваем масштаб, чтобы увидеть «тонкую структуру» распределения чисел:

Нумерология в MS SQL – занимательный эксперимент

Интересно, насколько точно мы можем выразить произвольное число, скажем, 1,23456789? Это определяется (половиной) максимальной длиной отрезка между двумя соседними точками (если нам не повезет).

Ниже эти расчеты показаны в виде графика, причем точность аппроксимации снижается дальше от нуля: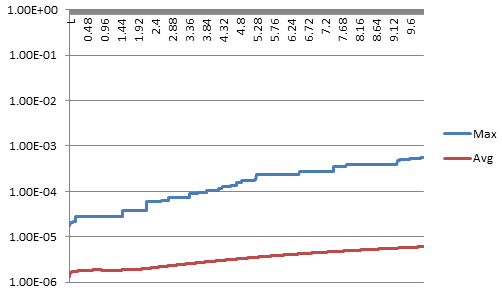

Нумерология в MS SQL – занимательный эксперимент

Таким образом, мы вообще можем выразить любое число с точностью от Е-6 до Е-5. Например, число 1,23456789 находится между cos(ln(3)/cos(3))+sin(1/ln(3)) = 1,23456481266341 (0,0002%) ln(exp(1)*sin(2))+exp(ln(3)/cos(3)) = 1,23456894186555 (0,000085%)

Нумерология в MS SQL – занимательный эксперимент

Наконец, мне интересно, что произойдет, если вместо A=1, B=2, C=3 взять другие числа, например, A=sqrt(2), B=e, C=pi. Сравнение плотности чисел в первом (123) и втором (2epi) вы можете увидеть на картинке:

Нумерология в MS SQL – занимательный эксперимент

Как видите, по большому счету, разницы нет. В заключение хочу рассказать, при чем здесь MS SQL. Проблема исчерпывающая, и просто напрашивается решение с перекрестными соединениями, которые реализуют декартово произведение всех доступных чисел для бинарных операций.

В конце вы можете увидеть небольшой фрагмент кода.

Полный код не публикуется, поскольку я хочу изменить его для автоматического создания текстов теории заговора на основе нумерологии.

   

   -- step 3
   insert into Formula (step,path,Value)
     select 3,path+' '+op,
         case 
           when op='COS' then COS(Value)
           when op='SIN' then SIN(Value)
           when op='EXP' then 
             case when Value<100 then EXP(Value) else NULL end
           when Value<=0    then NULL
           when op='LN'  then LOG(Value)
         end
       from Formula, Unary
   -- step 4  
   select L.path+' '+R.path+' '+'+' as path,L.value+R.value as value
     into p1
       from Formula L, Formula R
       where L.n<=R.n
   select L.path+' '+R.path+' '+'+' as path,L.value+R.value as value
     into p2
       from Formula L, Formula R
       where L.n<=R.n
   select L.path+' '+R.path+' '+'+' as path,L.value+R.value as value
     into p3
       from Formula L, Formula R
   select L.path+' '+R.path+' '+'+' as path,L.value+R.value as value
     into p4
       from Formula L, Formula R
       where R.value<>0

Теги: #астрономия #Популярная наука #Алгоритмы #Исследования и прогнозы в ИТ #ms sql server #наука #Microsoft SQL Server #математика #ms sql #Математика #нумерология