Этот небольшой ликбез я опубликовал довольно давно в своем Живом Журнале, но думал, что здесь он найдет больше заинтересованных читателей.
Децентрализованное управление H-бесконечностью с фиксированной структурой в MATLAB - так называется статья двух авторов (Паскаля Гаине и Пьера Апкаряна), о которой я хочу здесь кратко рассказать.
Поскольку я решил писать для относительно широкой аудитории, давайте предположим, что мы не знаем, что такое система управления.
Кому интересна тема поста, просьба пролистать текст до второй картинки.
Сначала от частного к общему.
Представим, что вам нужно наполнить ванну водой.
Но такой, чтобы вам не было невыносимо холодно и не обжигающе жарко.
Предположим, что у вас есть шаровой смеситель , и вы просто поднимаете балансир до упора, включив максимальный напор воды.
Одной рукой вы начинаете проверять температуру воды.
А другой перемещает качельку влево и вправо, чтобы обеспечить нужную температуру.
Это все вместе – вы, ваш кран и температура воды – и есть система управления.
У вас в голове есть представление о необходимой вам температуре воды.
Вы «меряете» рукой тот, который вам в данный момент подает кран.
А другой рукой стараетесь сделать так, чтобы разница между желаемой температурой и температурой водопроводной воды была минимальной.
На картинке это можно изобразить так: 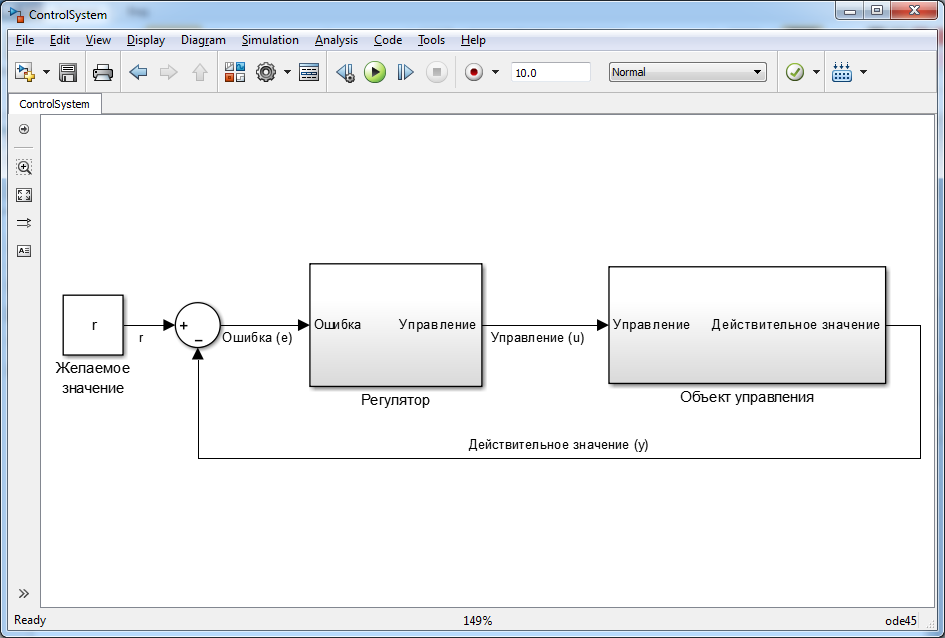
Рис.
1. Система управления в общем виде.
Фактически, то, что мы нарисовали выше, является фундаментальным представлением системы управления с обратной связью.
А на месте объекта управления (в нашем случае микшера) может быть что угодно.
А на месте регулятора (в нашем случае человека) может быть что угодно.
На картинке для простоты датчик (в нашем случае рука человека) не вынесен в отдельный блок, а включен в блок «Объект управления».
Сам объект не просто скажет, каково его текущее значение для параметра, который мы хотим изменить.
Также для простоты мы не вынесли исполнительный механизм в отдельный блок (тот, который помогает нам как-то влиять на объект управления – в нашем случае с другой стороны).
Сам объект тоже не просто изменится: на него нужно каким-то образом повлиять.
Берем из головы нужное значение температуры и называем его «теплым», хотя можем уточнить и сказать, что это, например, 20 градусов по Цельсию.
И отнимем от 20 значение температуры, которое получим с помощью датчика (наша рука под проточной водой).
Таким образом мы получим величину под названием «погрешность»: насколько температура водопроводной воды отличается от нужной нам температуры.
И с помощью регулятора (нашего мозга, где мы понимаем, делать нам теплее или холоднее) мы убедимся, что этой разницы не существует. Когда-то люди думали, что стоять у водопроводного крана (на самом деле это было довольно давно, а объектом было что-то другое) – занятие не слишком интересное.
И мы решили как-то автоматизировать получение нужного значения (в нашем случае температуры, но мы помним, что это может быть что угодно).
Поэтому стали появляться датчики (вначале механические - как, например, поплавок в, извините, бачке смыва унитаза, который "знает", сколько воды в бачке), затем электрические (для например, датчик температуры, который преобразует значение температуры в напряжение).
А раз у нас есть какая-то электрическая ценность, то почему бы не передать ее компьютеру, который сам будет думать, как чем-то управлять.
Мы просто скажем ему, какое значение мы хотим, и датчик скажет ему, какое оно есть на самом деле.
Итак, если немного подвести итоги, то задача человека, который занимается разработкой системы управления, состоит в том, чтобы придумать такие правила для этого компьютера, чтобы желаемое значение достигалось за короткое время и без лишних колебаний.
Поскольку иногда приходится контролировать не только температуру воды в кране, но и автомобили и вертолеты, сделать это может быть довольно сложно, поэтому просто логики (повернись туда, если) недостаточно.
А поскольку для регулятора приходится придумывать сложные уравнения, то было бы неплохо иметь такие уравнения для объекта (математической модели объекта).
Это может быть довольно сложно, когда имеется много контролируемых величин (много выходов) и много возможностей управления (много входов).
Точно так же, как в нашем примере.
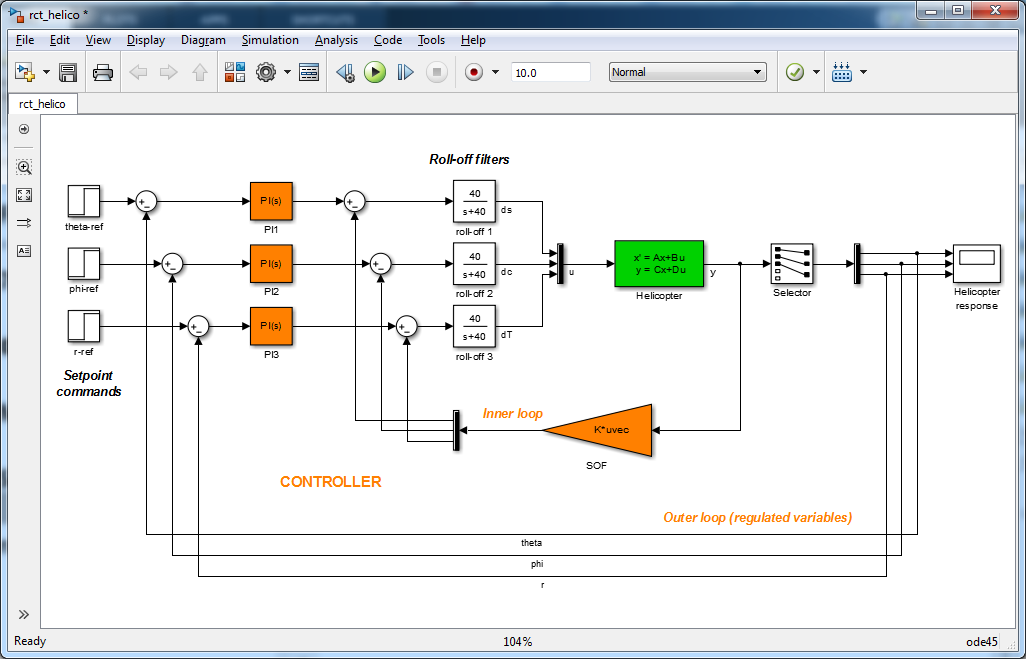
Рис.
2. Многоконтурная система управления вертолетом.
Здесь мы уже переходим к статье, ссылку на которую я дал в начале поста.
У нас есть объект управления — вертолёт (если интересно подробное описание, смотрите раздел 6 статьи).
У нас есть три входных сигнала (на рис.
2 они показаны одной линией перед зеленым блоком State Space под названием u. И пять выходных сигналов (строка после зеленого блока под названием y).
Мы выбрали такую структуру системы управления, что мы иметь три А ПИ-регулятор для управления тремя внешними цепями (оранжевые ПИ-блоки с цифрой в названии) и внутреннюю схему управления - для развязки каналов - с матрицей SOF (оранжевый треугольник).
Теперь осталось только задать требования к системе управления и каким-то образом выбрать 21 параметр нашей системы управления.
Авторы статьи предлагают методику, основанную на H-бесконечности.
Но при этом инженеру не обязательно знать, что такое H-бесконечность (если говорить очень упрощенно), чтобы сформулировать задачу.
Мы задаем требования в частотной области, говорим, что такие-то блоки нужно настроить в такой-то модели, что у нас есть управляющие сигналы и сигналы от датчиков.
И запускаем алгоритм, который подробно описан в статье.
В MATLAB 2012a (и 2011b, но не 2012b) есть пример, наглядно иллюстрирующий происходящее (по сути, мы можем повторить все, что происходит в статье).
Чтобы открыть скрипт, вы можете запустить команду редактирования helico_demo. Я взял на себя смелость записать видео, как это работает и какие результаты мы получаем (опять же просто повторю изложенное в статье).
В результате настраиваем 21 параметр и получаем стабильную систему, решающую задачу (развязка каналов и качество переходных процессов).
Графики сюда вставлять не буду - посмотрите статью.
Буду рад комментариям.
Теги: #matlab #системы управления #СКУД #simulink #simulink #MIMO #программирование #математика #matlab

-
Водные Растения
19 Oct, 24 -
Памятка Начинающему Почтмейстеру
19 Oct, 24 -
Топ-3 Html-Элемента, Которые Мы Забыли
19 Oct, 24 -
Геймпад Nes-Sega С Адаптером Usb
19 Oct, 24 -
Зачем Нужен Интернет На Кпк?
19 Oct, 24 -
Яндекс Рассортировал Блогосферу По Рейтингам
19 Oct, 24


