1. Об аттракторе Лоренца.

Эдвард Нортон Лоренц (1917 – 2008) – основатель теории хаоса, которая сегодня очень популярна в науке.
Он учился в Дартмутском колледже, Нью-Гэмпшир, США, и Гарвардском университете, Кембридж.
Во время Второй мировой войны он служил метеорологом в авиационном корпусе армии США, затем до конца своих дней работал профессором Массачусетского технологического института.
В 1963 году в Журнале атмосферных наук была опубликована его статья «Детерминированный непериодический поток» (русский перевод: Лоренц?.
Детерминированный непериодический поток // Странные аттракторы.
- М.
: Мир, 1981, с.
88-117).
.
которые заложили не только основы теории хаоса, но и изменили представления о моделировании погодных явлений.
В данной работе из системы уравнений Навье-Стокса впервые получена нелинейная автономная система обыкновенных дифференциальных уравнений третьего порядка (динамическая система), описывающая движение воздушных потоков в плоском слое жидкости постоянной толщины при разложении скорости потока и температуры в двойной ряд Фурье с последующим усечением до первой-второй гармоник: (1) 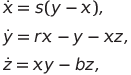
Где с , р И б — некоторые положительные числа, параметры системы.
Обычно исследования системы Лоренца проводятся при с = 10 , р = 28 И б = 8/3 (классические значения параметров).
В общем, теория хаоса — это раздел математики, изучающий поведение детерминированных динамических систем, где решения имеют довольно сложную структуру, поэтому кажется, что они ведут себя случайным образом с течением времени.
Детерминированная система - это система, уравнения движения, параметры и начальные условия которой известны и не являются случайными (Мун Ф.
Хаотические колебания.
- М.
: Мир, 1990).
Динамическая система (1) возникает и в других процессах: 1. Конвекция в тороидальной трубе (Ланда П.
С.
Нелинейные колебания и волны.
- М: ЛИБРОКОМ, 2010, стр.
454-455); 2. Одномодовый лазер (Покровский Л.
А.
Решение системы уравнений Лоренца в асимптотическом пределе большого числа Рэлея.
I. Система Лоренца в простейшей квантовой модели лазера и применение к ней метода усреднения // Теоретическая и математическая физика, 1985, т. 62, вып.
2, стр.
272-290); 3. Генератор с инерционным возбуждением (Неймарк Ю.
И.
, Ланда П.
С.
Стохастические и хаотические колебания.
- М: ЛИБРОКОМ, 2009, стр.
288-295).
Для любого решения системы Лоренца существует момент времени, когда соответствующая фазовая траектория навсегда погружена в сферу фиксированного радиуса.
Следовательно, существует предельное множество — аттрактор Лоренца, к которому притягиваются все траектории динамической системы при 
(Немыцкий В.
В.
, Степанов В.
В.
Качественная теория дифференциальных уравнений.
- М.
: Редакция УРСС, 2004, стр.
357-359).
Таким образом, аттрактор определяет поведение решений системы (1) на больших промежутках времени.
Из-за отсутствия точных методов решения нелинейных динамических систем общего вида для анализа структуры аттрактора часто используют численные методы, такие как, например, сочетание явной схемы Эйлера с центральной разностной схемой Адамса.
, использование высших производных, а также 4-го порядка Рунге-Кутты.
В случае классических значений параметров системы наблюдается неустойчивость ее решений, так как положения равновесия системы имеют седловой тип.
Это ограничивает использование этих методов, поскольку суммарная ошибка увеличивается с увеличением интервала интегрирования.
Таким образом, небольшие изменения начальных условий системы (1) (т.е.
атмосферы) со временем могут привести к значительным последствиям.
В 70-х годах XX века Гукенхаймер, Уильямс и Йорк на основе результатов численных экспериментов сформулировали гипотезу о структуре аттрактора Лоренца для классических значений параметров системы, однако соответствие этой гипотезы структура притягивающего множества системы (1) строго не доказана.
В 2000 году Стивен Смейл составил список 18 наиболее значимых математических задач XXI века.
Проблема о строении аттрактора Лоренца вошла в этот список под номером 14. Считается, что это была решено Уорвик Такер в 2002 году использовал интервальную арифметику, но многие математики не приняли его доказательство хотя бы потому, что наличие периодических решений в системе (1) не было строго доказано.
В литературе, посвященной численному исследованию системы Лоренца с классическими значениями ее параметров, часто делаются выводы о структуре аттрактора на основе данных, полученных в результате вычислительного эксперимента (например, о том, что аттрактор содержит циклы).
При этом нет достаточного обоснования выбора шага, с какими типами действительных чисел приходилось работать и за какой период времени проводились расчеты.
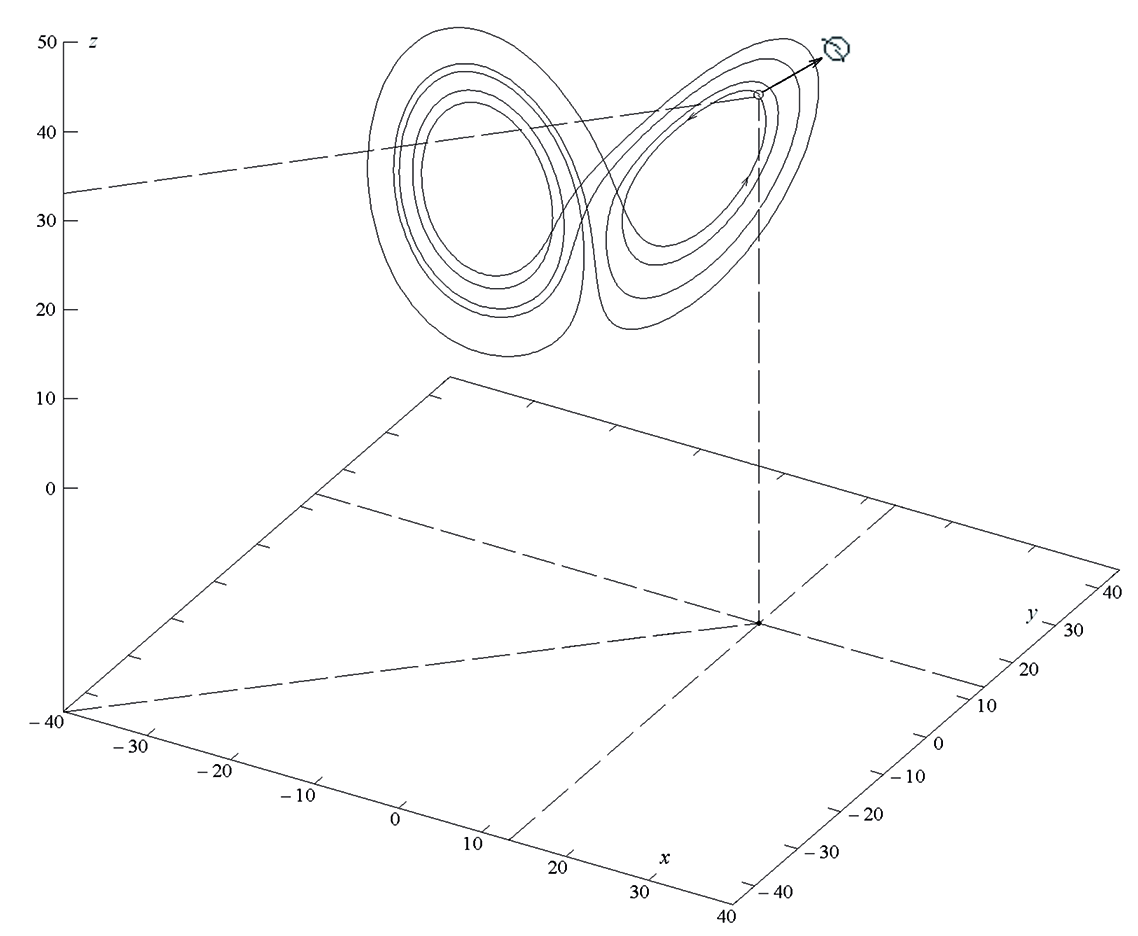
Рис.
1. Дуга траектории, построенная на интервале времени [0;6,827] для x(0)=13,41265629, y(0)=13,46430003, z(0)=33,46156416. Согласно теореме Биркгофа (Немыцкий В.
В.
, Степанов В.
В.
Качественная теория дифференциальных уравнений.
- М.
: Редакция УРСС, 2004, с.
402), аттрактор Лоренца содержит возвратные траектории, и каждое возвратное движение устойчиво по Пуассону.
Это означает, что существуют сколь угодно большие значения моментов времени, такие, что точка траектории системы оказывается в любой окрестности ее начального положения.
Таким возвратным движением может быть и цикл, но сделать вывод об этом на основании найденного возврата траектории в некоторую окрестность начальных условий невозможно.
Как показали расчеты (рис.
1), в системе Лоренца динамика поведения решений на аттракторе достаточно сложна - содержащиеся в ней рекуррентные траектории могут, например, описываться почти периодическими решениями или иметь более сложную состав.
Построен мной пример неавтономная система с таким поведением решения.
2. Моделирование динамики системы Лоренца.
Рис.
2. Схема генератора колебаний, описывающая динамику системы Лоренца.
Для генерации сигналов (хаотических колебаний), описывающих траектории на аттракторах динамических систем с определенными видами нелинейностей правых частей, на практике также применяется физическое моделирование с использованием электрических схем /или аналоговых компьютеров/ (Дмитриев А.
С.
, Панас А.
И.
Динамический хаос: новые носители информации для систем связи - М.
: Физматлит, 2002).
Рассмотрим электрическую схему генератора колебаний, представленную на рис.
2, как альтернативу численному моделированию.
Поскольку система Лоренца имеет третий порядок, для создания динамики изменения напряжения в схеме необходимы три интегратора на базе операционных усилителей, поскольку с дифференциаторами связаны проблемы с шумами.
При этом для построения схемы и записи интегральных уравнений была использована базовая схема подключения современного аналогового умножителя.
MPY634 , показанный на рис.
3 в официальная документация производитель чипов.
У нас есть: 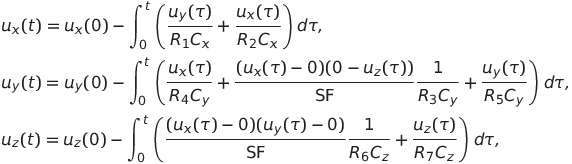
Где 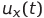
, 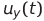
И 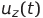
— мгновенные значения напряжения, соответствующие функциям Икс ( т ) , й ( т ) И я ( т ) (пару этих напряжений можно подать на обкладки осциллографа – полученная комплексная фигура является проекцией траектории системы Лоренца на соответствующую плоскость), 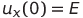
И 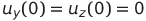
— начальные напряжения на конденсаторах 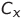
, 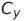
И 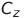
соответственно, СФ = 10 В — масштабный коэффициент множителя.
Конденсатор изначально заряжен.
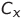
от источника питания ? ; резистор 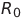
предусмотрена для подзарядки (ключевое состояние К показано на рисунке в схеме генератора).
Остальные конденсаторы имеют нулевой начальный заряд. По сути, мы задаем начальные условия для системы (1).
Первоначальную схему зарядки можно изменить (например, зарядив два конденсатора), за исключением ситуации, когда 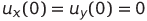
.
Это объясняется 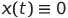
, 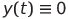
И 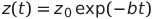
является частным решением системы (1), где 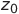
— произвольная константа.
Понятно, что в этом случае колебаний не будет.
Давайте сделаем замену 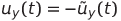
и дифференцируем по времени обе части каждого интегрального уравнения.
Мы получаем (2) 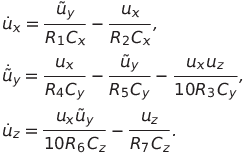
Моделировать динамику будем для классических значений параметров системы (1).
Примем значения сопротивлений и емкостей равными 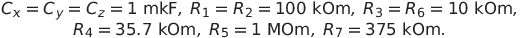
Тогда система (2) примет вид (3) 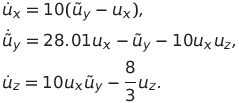
Делаем замену в (3) 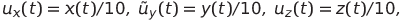
получаем систему Лоренца.
Поскольку 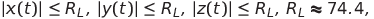
то из введенной замены следует, что абсолютное значение напряжения не превысит значения 7,44 В , что предусмотрено в документации на умножитель MPY634 .
Значение ? можно выбрать равным 1,5 В (батарейка DS AA).
Точность представленной модели определяется погрешностями реальных емкостей и сопротивлений, а также частотными характеристиками интеграторов и умножителей.
P.S.
Недавно я выступал с докладом на эту тему на математической конференции.Вы можете посмотреть это Здесь (заранее извиняюсь за качество видео).
Там же можно скачать материалы доклада (презентацию лучше просматривать синхронно с докладом, так как из-за качества видео ее не видно).
Теги: #аттрактор Лоренца #система Лоренца #дифференциальные уравнения #периодические решения #численные методы #аналоговый умножитель #операционный усилитель #операционный усилитель #интегратор #математика

-
Путеводитель По Devops С Express 42
19 Oct, 24 -
Каким Walmart Видит Супермаркет Будущего
19 Oct, 24 -
Зеленая Энергетика И Ядерный Кремний
19 Oct, 24 -
Коротко О Нексусе
19 Oct, 24 -
Первый В Мире Однокристальный Трансивер
19 Oct, 24


