Введение
Приветствую вас, дорогие читатели! Сегодня я предлагаю вам задуматься над следующей проблемой:
Данный

пары точек на плоскости

.
Все
разные.
Нужно найти многочлен
такой, что
, Где
В переводе на русский имеем: Иван загадал желание
точки на плоскости, и Мария, учитывая эту информацию, должна придумать функцию, которая (как минимум) будет проходить через все эти точки.
В текущей статье наша задача сводится к тому, чтобы окольным путем помочь Марии.
— Почему окольным путем? - ты спрашиваешь.
Ответ традиционный: данная статья является продолжением серии дилетантских статей о математике, целью которых является популяризация математического мира.
Процесс
Для начала стоит отметить, что определенное количество интерполяционные полиномы уже существует, конечно.Эти полиномы точно предназначены для решения желаемой задачи.
Среди них наиболее известными являются многочлены Лагранж И Ньютон .
Также необходимо уточнить, что такое «произвольные функции» (термин взят из названия настоящей статьи).
Они означают любую унарную функцию, результат которой равен биективное отображение аргумент.
В рамках статьи предлагаю взять за такую функцию десятичный логарифм
и следующие моменты:
Изобразив их на плоскости, у вас должно получиться что-то вроде этого: 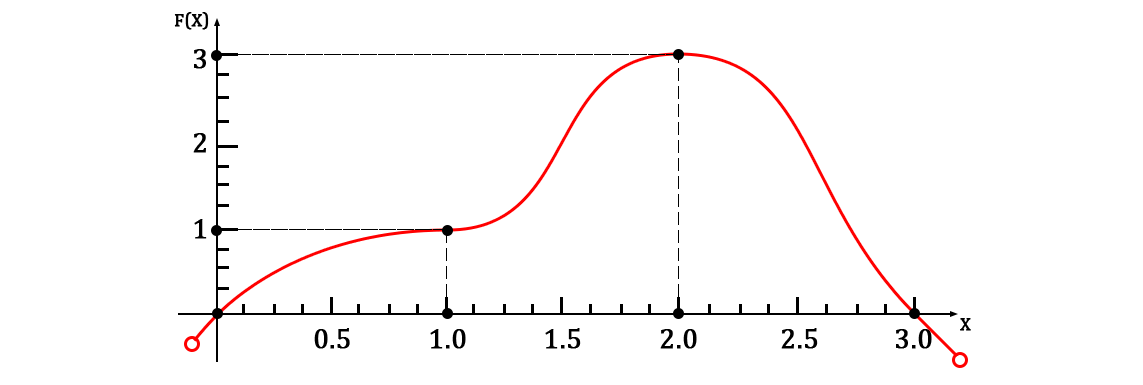
Легко видеть, что теперь число пар точек равно
.
При решении этой задачи на ум приходит некая система уравнений, где число линейно независимый линии равны
.
Что это за система уравнений?
Попробуем записать функцию в виде суммы десятичных логарифмов с коэффициентами при них (так, чтобы количество коэффициентов было равно
):
Аргументы за
разные, чтобы избежать линейной зависимости строк в будущем (можно придумать и другие).
А также, учитывая, что область определения функции не менее
(исходя из точек, заданных условием), мы тем самым обеспечиваем существование диапазона значений функции
в этой области определения.
Поскольку мы знаем
пары точек, то обратимся к ним, чтобы построить следующую тривиальную систему:
Тривиальность системы заключается в том, что мы просто находим такие
, который будет удовлетворять всему набору условий.
Действительно, решение этой системы относительно
мы получаем следующее решение:
Это, естественно, завершает задачу; остается только записать это в одну функцию:
Разумеется, оно пройдет через заданный набор точек.
И график функции будет выглядеть так: 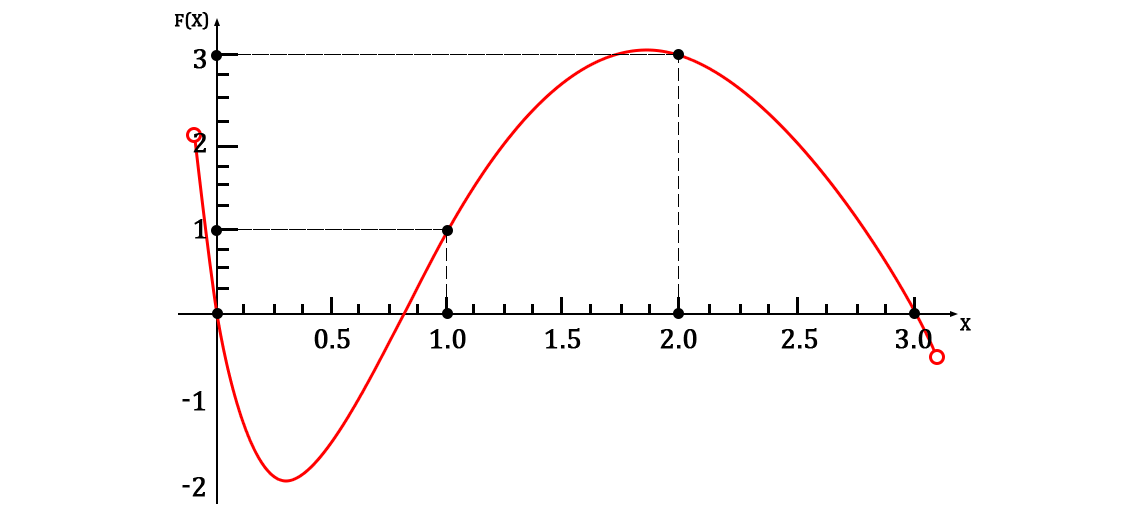
Также для наглядности можно привести примерную систему решений:
Тогда приближенный вид функции будет следующий:
Конечно, никто не говорит, что полученная функция будет минимальной (тот же полином Лагранжа даст более короткую форму).
Однако этот метод позволяет выразить функцию через набор произвольных функций (правда, с учетом ограничений, указанных выше в статье).
Различные примеры
На десерт давайте аналогичным образом создадим функцию в радикалы :Составим систему уравнений для нахождения коэффициентов:
Его решение уникально и выглядит так:
Тогда готовая функция будет выглядеть так:
Что также является полиномом Лагранжа для данного набора точек (поскольку неявно реализует радикальную форму алгоритма из статьи).
График площади заданных точек выглядит следующим образом: 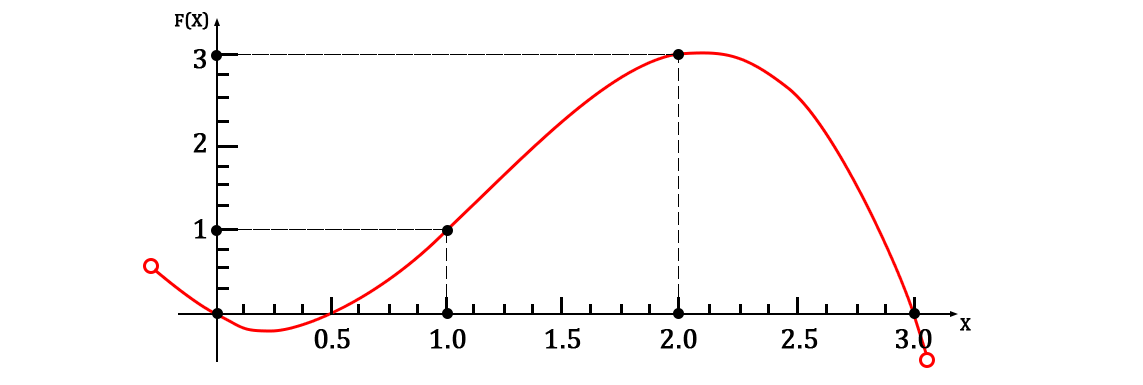
Самое интересное в этой истории то, что произвольные функции можно и нужно объединять для построения итоговой функции.
Другими словами, функция может быть построена непосредственно на радикалах и логарифмах, а может и на чем-то другом (показательных функциях, факториалах и т. д.).
Лишь бы полученный набор функций обеспечивал линейную независимость строк при выборе коэффициентов.
В общем, для данного
пар точек это выглядит так:
Где
– коэффициенты, которые необходимо найти через систему уравнений (СЛАУ), а
— некоторые функции, которые обеспечат линейную независимость при нахождении коэффициентов.
А дальше – по алгоритму выше, все полностью аналогично.
Не забывая об этом
должна определяться в точках, указанных условием.
Например, вы можете показать функцию, состоящую из совершенно разных базовых функций:
Чтобы удовлетворить заданному набору баллов, коэффициенты тогда будут следующими (находятся строго по алгоритму из статьи):
А сама функция будет такой:
График будет выглядеть практически так же, как и предыдущий (в районе заданных точек).
Если вам нужен более «гладкий» график, вы можете посмотреть в сторону факториала, например так:
Найдем коэффициенты:
Подставим их в готовую функцию:
Давайте также полюбуемся очень хорошим графиком: 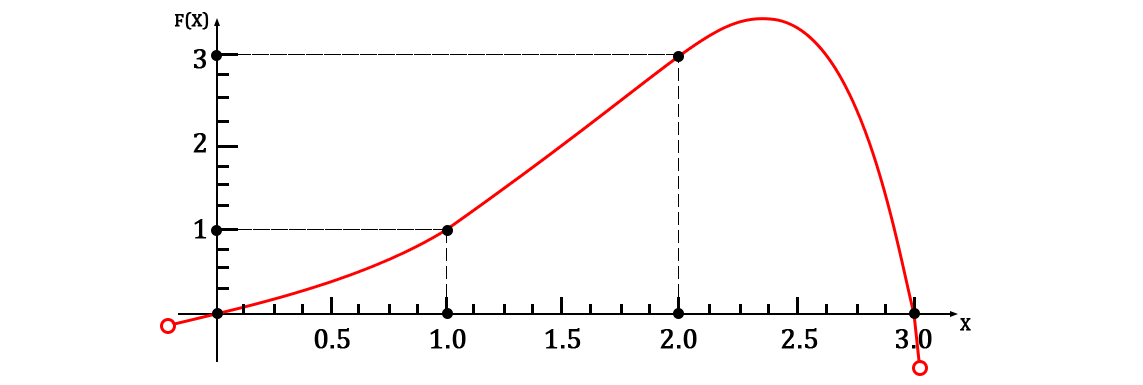
Почему это необходимо?
Да хотя бы представить пучок веревок, связанных пластиковыми хомутами :)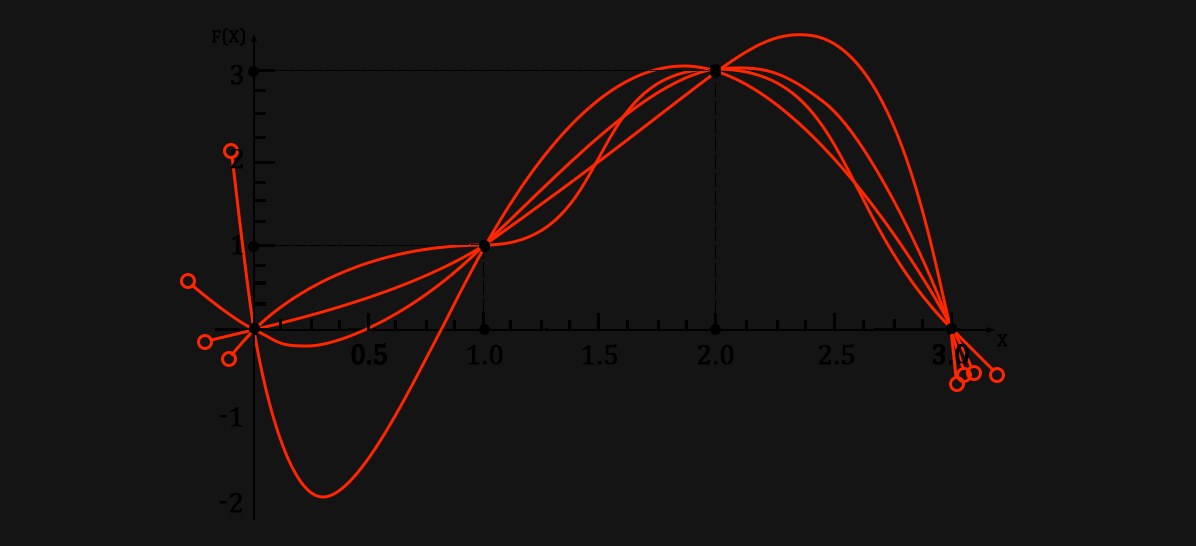
( * Здесь мы просто наложили все графики друг на друга ) На этой статье все, рекомендую поиграться самостоятельно.
Всего наилучшего, Питер был с тобой.
Теги: #математика #уравнения #уравнения #полином #полином #функция #интерполяционный полином #Лагранжа #Ньютон #точки #график #Алгоритмы #математика
-
Обзор Модульного Программирования
19 Oct, 24 -
О Вступлении В Силу «Антипиратского» Закона
19 Oct, 24 -
22 Ноября, Москва – Analyit Meetup №3
19 Oct, 24


