Сначала я хотел не углубляться в тензоры и описывать их вскользь, затрагивая только используемый мной функционал.
Однако я передумал и решил рассказать больше.
Добро пожаловать в многомерный мир.
Часть 1 Здесь Список сокращений CP - КАНДЕКОМП/ПАРАФАК
CANDECOMP - Каноническое разложение
PARAFAC – параллельные факторы
ПАРАТКУК2 - ПАРАФАК/Такер2
ALS — чередующиеся наименьшие квадраты
PMLS — метод чередующихся наименьших квадратов
SVD — Разложение по сингулярным значениям
СЛАУ — Система линейных алгебраических уравнений
GFDM — обобщенное мультиплексирование с частотным разделением каналов.
SECSI — SEmi-алгебраическая структура для приближенного разложения eCP посредством одновременной диагонализации матрицы Используемые обозначения Скалярные величины обозначаются строчными буквами без жирного шрифта, например: 
Жирные строчные буквы обозначают векторы.
Так: 
Заглавные буквы, выделенные жирным шрифтом, используются для обозначения матриц.
Так: 
Тензоры обозначаются заглавными каллиграфическими буквами.
Так: 
Нижние индексы указывают положение в матрице в строках и столбцах.
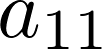
В разработках индексы сообщают о расширяемом пространстве.

Индексы в тензорах обозначают фронтальный срез тензора, если не указано иное.

Тензоры
Возможно, лучшим определением тензора является цитата Тамары Г.Колда:
Тензор — это многомерный массивЭто не могло быть проще.
Идеи с тензорами возникли изначально в линейной алгебре.
Поэтому лучший способ — описать все с помощью линейной алгебры.
В линейной алгебре мы используем скаляры, векторы, матрицы и можем выполнять операции сложения, вычитания и умножения.
Скаляр состоит из 1 элемента, вектор состоит из Н элементов, а матрица состоит из Миннесота элементы.
Тензоры включают в себя все, что может линейная алгебра, и даже немного больше.
Привожу примеры из линейной алгебры: вектор – это тензор первого порядка, а матрица – тензор второго порядка.
Следовательно, порядок тензора определяется количеством пространств, в которых тензор имеет более одного элемента.
Чем больше у вас пробелов, тем выше порядок тензора.
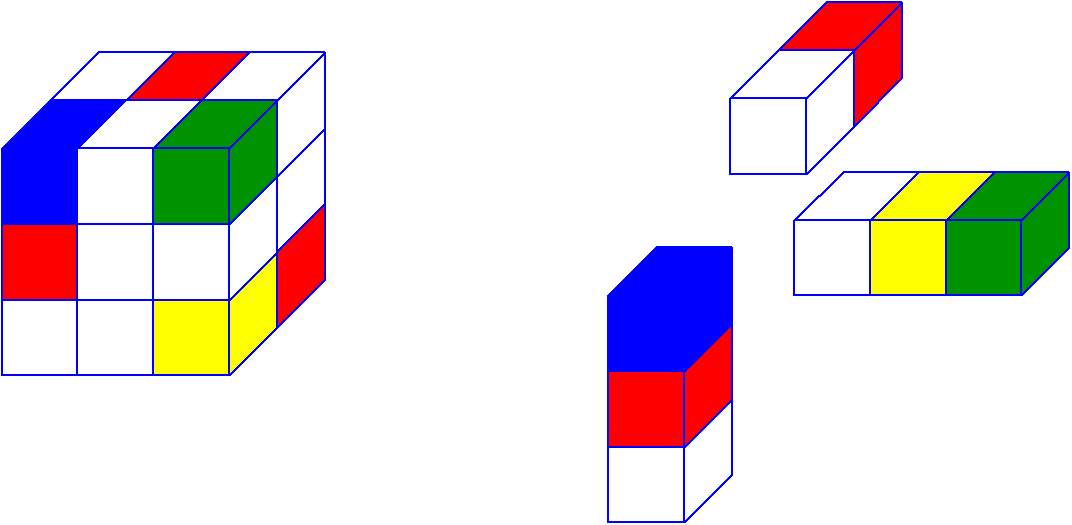
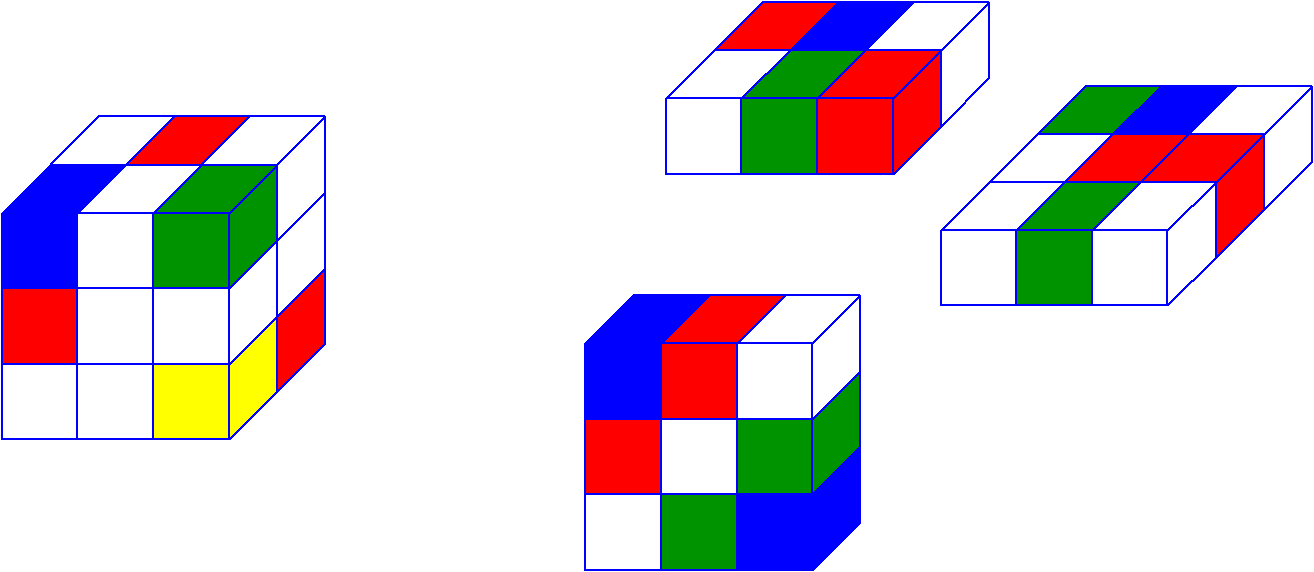
Достаточно просто, не так ли? Сразу приведем пример тензора третьего порядка.
Познакомьтесь с этим тензором, с которым вы будете работать сегодня, и увидите в нем немного тензорной магии.
Ниже я расписал его фронтальные разрезы.
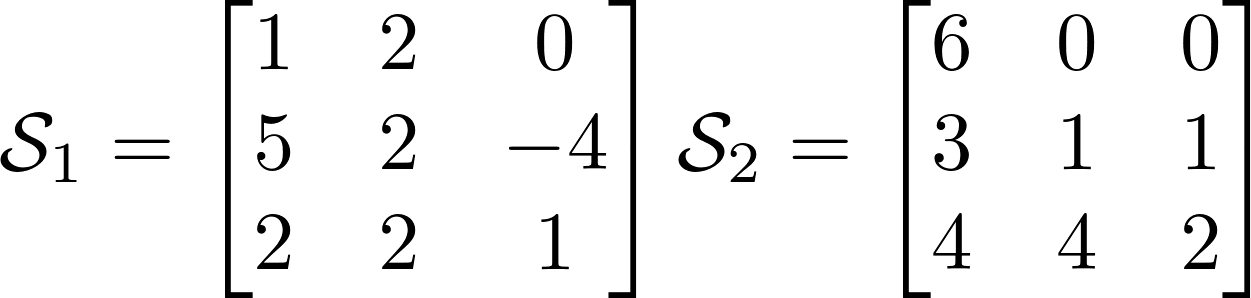
Линейная алгебра дает нам произведение двух матриц следующим образом: ![]()
Этот продукт имеет два измерения, и операция между объектами с размерностью больше двух не определена.
Тензорная алгебра предоставляет инструменты для преодоления этого ограничения за счет использования возможностей большего количества пространств в линейной алгебре.
Для начала я представлю три матричные операции, без которых в тензорной алгебре нельзя сделать шаг: Продукт Кронекера Итак, произведение Кронекера (или, как его еще называют, тензорное произведение) включает в себя две матрицы, результатом их произведения будет блочная матрица, каждый блок которой представляет собой вторую матрицу, умноженную на определенный элемент первой матрицы.
.

Эта операция используется для формирования упрощенной модели канала в MIMO. работа Хатри-Рао Произведение Хатри-Рао обозначается следующим символом и является произведением Кронекера для всех соответствующих столбцов.
Другими словами, каждый я й столбец матрицы А умножается на я й столбец матрицы Б и результат я й столбец полученной матрицы.

Эта операция чаще всего используется в тензорах третьего порядка; например, именно через него я описал матрицу модуляции системы GFDM Произведение Адамара Произведение Адамара является самым простым из всех, оно представляет собой поэлементное произведение всех позиций в матрицах.
А И Б .

Основные операции в тензорной алгебре
Сканировать
В тензорной алгебре одним из ключевых понятий является «развёртывание» (я буду называть это развёртыванием для уменьшения англицизмов) или представление тензора через матрицу.Развертывание — это отображение тензора на одно из его пространств.
При этой операции тензор записывается в виде матрицы, количество строк которой равно количеству элементов развернутого пространства.
«Элементы в строке имеют одинаковый порядковый номер в заданном пространстве.
особенность Существует два типа записи элементов в строку: нотация Латауэра и нотация Matlab. Наиболее часто используемая нотация — Matlab, поэтому я буду использовать ее.
Согласно обозначениям Matlab, элементы располагаются в порядке возрастания размерности, т.е.
сначала элемент идет по первому измерению, затем по второму и так далее, исключая расширяемое измерение.


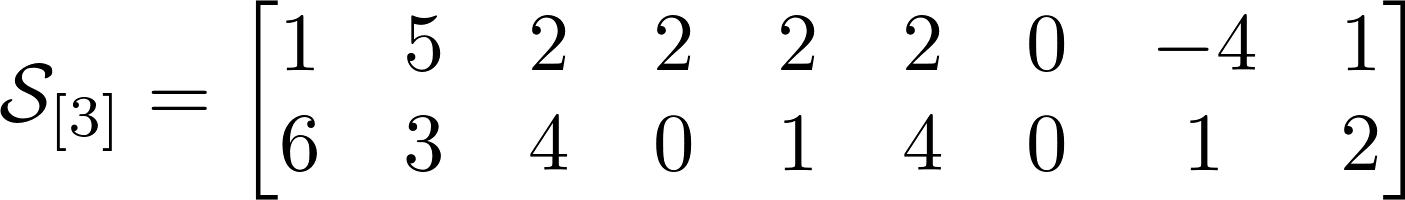
Число возможных разработок равно порядку тензора или его размерности.
Тензор из нашего примера имеет 3 развития.
Выше представлены разработки для нашего тензора, и я надеюсь, что они вам будут гораздо проще понять, чем пояснения.
Тензоры мне показались гораздо более понятными в интуитивном смысле, чем в плане определений.
Продукт в заданном пространстве
Следующая операция, которую я хочу описать, — это произведение тензора на матрицу в заданном пространстве.Она записывается следующим образом и по сути представляет собой произведение двух матриц, где правая матрица — это развертка тензора по умножаемому пространству, а левая — матрица, на которую собственно и происходит перемножение.
![]()
Важным моментом является то, что умножение записывается справа, а происходит слева от тензора.
В результате получается матрица, представляющая собой развитие нового тензора, который можно собрать обратно в знакомый тензор.
Важно отметить, что в результате этой операции размерность пространства, с которым происходит умножение, может измениться , остальные не могу .
Пример ниже 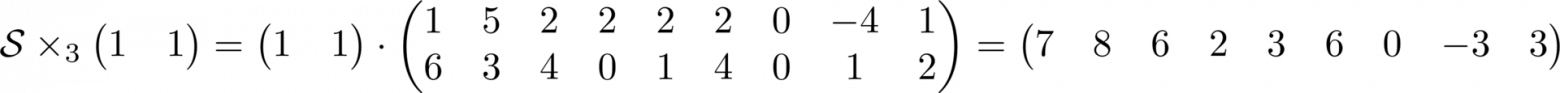
Тензор первого ранга
Тензор первого ранга – это тензор размерности Н , который можно получить, умножив единицу на Н векторы, по одному на каждое пространство.Ниже я показал, как это выглядит визуально для тензора третьего порядка.
Тензор первого ранга — это аналог одной компоненты для SVD-матрицы, где комплексная матрица разлагается на матрицы одного ранга.
Тензор ранга один может быть как комплексным, так и вещественным, в зависимости от требований, которые мы к нему предъявляем.
![]()

Тензорное разложение
Самое важное и интересное в тензорах — это их разложение.Надеюсь, многие из вас знают или слышали о разложении матрицы на сингулярные значения.
С его помощью мы можем представить матрицу как сумму матриц первого ранга и оценить их вклад в общую матрицу.
Ниже приведен пример такого разложения.

В тензорной алгебре есть очень похожий аналог, он называется «CP», его еще называют «CANDECOMP» или «PARAFAC».
«CP» разлагает любой тензор в сумму тензоров первого ранга.
Эта формулировка имеет две формы обозначений: простая из которых фактически записывает тензор как сумму набора тензоров первого ранга, другая записывает разложение через матрицы по каждому из пространств.
Помимо «СР»-разложения в тензорной алгебре существует большое количество его аналогов, зависящих от нормировки компонент и других особенностей.
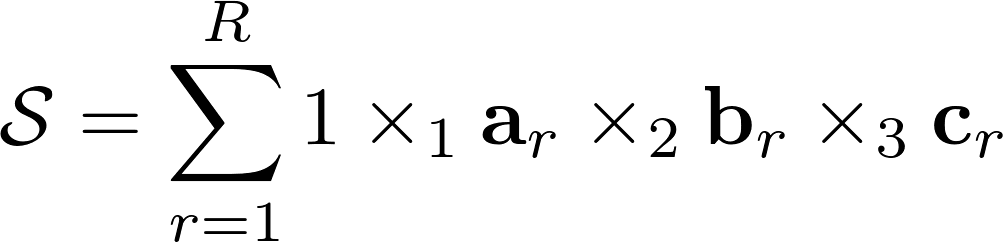

Смотрите, если написать векторы каждого из пространств друг за другом, то получится N матриц.
Каждая из матриц представляет собой некую «базу» в своем пространстве.
Такая форма записи напоминает матрицы СВД.
Из этих матриц можно получить обратно тензор, если взять единичный тензор и поочередно умножить его на все базисные матрицы по пространствам.
![]()
Легко вывести выражение развития из разложения тензора третьего порядка; это позволит разделить одну из матриц обычным матричным произведением.
Посмотрите ниже, вы видите матрицу А записывается через произведение с другой матрицей, которая, в свою очередь, является произведением произведения Хатри-Рао.
Зная продукт продукта и исходную разработку, мы можем рассчитать матрицу А с помощью линейной алгебры.
Это значительно упрощает работу алгоритмов расчета разложения тензоров третьего порядка и дает удобные формулы для итераций.
![]()
Зачем вообще нужна эта ерунда? Мы могли бы сделать сканирование СВД? Конечно, могли бы, но в общем случае тензорная декомпозиция значительно упрощает описание данных, их становится проще сжимать или находить закономерности.
Это особенно важно для больших объемов данных, поскольку с увеличением размерностей ранг меняется гораздо меньше.
Проблемы разложения
У этого разложения, несмотря на всю его прелесть, есть две проблемы.Первое: вам нужно самостоятельно узнать ранг этого расширения.
Часто это нетривиальная задача, особенно если данные зашумлены.
Пример из моего опыта Ось ординат представляет нормализованную ошибку реконструкции, а ось абсцисс представляет использованный ранг разложения.
Я расширил тензор только суммой сигнала и шума и только шума.
Предположение о ранге пришлось сделать только из-за необычного поведения ошибки декомпозиции.
Внимание, легенда перепутана.

Алгоритм заключался в поиске сигнала GPS при вычислении корреляции с использованием многофазного преобразования Фурье.
При этом размерность выходных данных на корреляторе была равна четырем (время, частота, код, сдвиг полифазного преобразования).
Вторая проблема – это расчет самого расширения.
Самый распространенный алгоритм на данный момент: А.
Л.
С.
или ПМНК .
Еще есть алгоритм с романтическим названием СЕКСИ , но об этом, возможно, расскажу в будущем.
ПМНК или метод попеременных наименьших квадратов возмутительно прост, его алгоритм следующий:
- Установите ранг разложения
- Генерация матриц разложения случайного пространства
- Фиксируем все матрицы кроме одной и вычисляем оставшуюся матрицу с помощью СЛАУ
- Повторяем предыдущий пункт поочередно для всех матриц до тех пор, пока расхождение не станет допустимым.
Этот метод имеет огромное количество недостатков, включая локальные минимумы и вычислительную сложность, но по-прежнему остается одним из наиболее используемых алгоритмов в настоящее время.
Связаться с GFDM

Теперь давайте подойдем ближе к технологии GFDM. Существует еще одно разложение, называемое PARATUCK2, и это аббревиатура двух других сокращений «PARAFAC» и «TUCKER2».
Да, аббревиатура, состоящая из двух других аббревиатур, как это чудесно.
Это разложение записывает тензор в виде трех матриц и двух тензоров.
Матрица в середине называется ядром разложения, тензоры — объединяющими тензорами.
Последние две матрицы не имеют специального названия.
Другое дело, как вычислить тензор из этого разложения.

Тензор от разложения вычисляется послойно, в каждом слое выбирается только соответствующий слой тензоров отношений.
В результате получается 5 матриц, умножая которые получаем значения тензора.
Эта операция повторяется для каждого из слоев, а результаты собираются один за другим.
Количество строк первой матрицы равно количеству строк тензора, аналогично столбцам третьей матрицы и тензора, а также глубине тензоров связей.
Поначалу мне было очень трудно это понять.
И что самое интересное, эта модель действительно может помочь вам при анализе данных.
Так зачем нам это разложение? Он довольно сложный и состоит из пяти элементов, чем он вообще может помочь с GFDM? Давайте сначала вспомним и немного закрепим информацию о GFDM. Ниже приведен метод генерации символов, который отправляет передатчик.
Блок данных может быть сформирован в виде матрицы, где строки представляют собой поднесущие, а столбцы — временные позиции в блоке.
Общий блок данных получается суммированием всех элементов, другими словами, нам нужно поэлементно умножить вектор поднесущей на вектор оконной функции и все это на тот символ, который мы передаем.
Таким образом, каждый символ находится на пересечении двух векторов, на которые он умножается.
Операция довольно проста, но ее сложно описать через произведение матрицы модуляции и вектора символов.
Форма записи через матрицу модуляции является основным элементом построения приемников.

Если присмотреться, PARATUCK2 действительно может описать GFDM. Для этого необходимо в качестве крайних матриц взять единичные векторы-строки и векторы-столбцы, а к тензорам связей вдоль главных диагоналей добавить оконные функции и поднесущие.
Если в основной матрице есть символы, результатом будет вектор в третьем измерении, соответствующий передаваемым данным.
Пример из опыта Изначально я намеревался дополнительно описать частотно-зависимый канал канала через значения в векторе рядом с тензором поднесущей.
Это было ошибочное предположение 
Умно завернуто, не так ли? Когда я писал диссертацию, было сложно понять, как это можно упростить и привести к приемлемому виду, но это возможно! Благодаря этому разложению можно упростить выражение матрицы модуляции в произведение двух матриц.
Однако, думаю, я расскажу вам в следующий раз вместе с теорией нулевого принуждения, согласованного фильтра и приемников с минимальной среднеквадратичной ошибкой.
Рекомендации Т.
Г.
Колда и Б.
В.
Бадер, Тензорные разложения и приложения», SIAM Review, том.
51, нет. 3, стр.
455{500, 2009. Р.
Бро, Н.
Сидиропулос и Г.
Яннакис, \ Parafac: Учебное пособие и приложения.
Группа хемометрики, пищевые технологии, Королевский ветеринарный сельскохозяйственный университет, 1997. Л.
де Латаувер, Б.
де Моор и Дж.
Вандервалле, \Мультилинейное разложение сингулярных значений.
позиция», SIAM J. MATRIX ANAL. APPL. Том 21, № 4, стр.
1253–1278, 2000. К.
Б.
Петерсен и М.
С.
Педерсен, «Матричная кулинарная книга».
Петерсен и Педерсен, 2012. С.
ЛЮ и Г.
ТРЕНКЛЕР, Адамар, Хатри-Рао, Кронекер и др.
Матрица продукты», МЕЖДУНАРОДНЫЙ ЖУРНАЛ ИНФОРМАЦИОННЫХ И СИСТЕМНЫХ НАУК.
ЭНСЕС, 2006. А.
Л.
Ф.
де Алмейда, Г.
Фавье и Л.
Р.
Хименес, \ Пространство-время-частота (stf) mimo системы связи со слепым приемником на основе обобщенной модели paratuck2», IEEE Transaction по обработке сигналов, том.
61, нет. 8 апреля 2013 г.
Хорошей недели.
В опросе могут участвовать только зарегистрированные пользователи.
Войти , Пожалуйста.
Хотите узнать, в каком университете я получил такие знания? 66,4% Да 83 33,6% Нет 42 Проголосовали 125 пользователей.
44 пользователя воздержались.
Теги: #Популярная наука #математика #Будущее здесь #Сотовая связь #обработка данных #тензоры #линейная алгебра #gfdm

-
Дублирование Компакт-Дисков: Обзор
19 Oct, 24 -
Рекомендации – Релиз (Альфа)
19 Oct, 24 -
Apple-Пингвин Захватил Офис Microsoft.
19 Oct, 24 -
«Ведомости» Выставляют «Подложку»
19 Oct, 24


