Особенности систем координат на точечной основе ( ди- и бикоординаты ) заключается в том, что их можно использовать как в обычном геометрическом пространстве, так и в пространстве графов.
Оглавление 1. Симплексы и графы 2. Определение ди- и бикоординат. 3. Скалярное произведение пар
4. Графовое пространство 5. Трансформация базы 6. Количество звезд 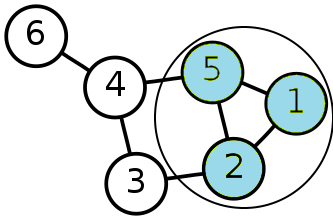
Что такое пространство графа
Размерность пространства и размерность основы
Размерность пространства графа определяется количеством его связных вершин (будем считать, что все вершины графа связны – граф однокомпонентный).Пространственный базис определяется как подмножество вершин графа с известными расстояниями между ними (метрикой).
Подмножество может включать все вершины графа или только часть (подграф).
В последнем случае размерность базиса меньше размерности всего графового пространства.
Ээлементы в графовом пространстве
Необходимо понять, что представляют собой элементы и векторы на графике.Граф — это совокупность связанных элементов (узлов).
Узлы графа определяют его набор потенциальных базовых элементов, а связи определяют метрику, расстояние между базовыми элементами.
В качестве основы для определения системы координат на графе можно выбрать не все узлы графа, а только его часть — базисный подграф.
В этом случае все пространство графа можно разделить на два подпространства – основное и внебазовое (внешнее).
Узлы, входящие в основу графа, называются базовыми.
Все остальные элементы пространства задаются относительно его базовых узлов через барицентрические координаты (веса базовых вершин).
В общем случае элемент может либо принадлежать базисному пространству, либо находиться вне его.
Ээлементы вне базиса будут называться внешний .
Поскольку внешний элемент имеет ненулевое расстояние до базисного пространства, каждый внешний элемент является узлом графа, не входящим в его базис.
То есть внешние элементы явно указаны в структуре графа.
В структуре никак не появляются элементы, принадлежащие базисному пространству — виртуальные элементы (за исключением явно заданных вершин базиса).
Норма виртуальных элементов равна нулю — это просто вектор потенциалов в вершинах базиса, нормированный на единицу.
Примером виртуального элемента базисного пространства является ортоцентр базиса.
Если граф представляет собой электрическую цепь, то элементом является совокупность потенциалов в узлах сети.
Лапласиан электрической цепи представляет собой матрицу, состоящую из краевых проводимостей.
Умножение этой матрицы на электрические потенциалы узлов дает ток в узлах.
Соответственно, потенциалы в узлах являются координатами расстояний
, а полный ток узла барицентричен:
.
Преобразование координат просто отражает Закон Ома :
В отличие от обычного восприятия пространства, в котором элементы являются чем-то материальным, а их компоненты виртуальными (веса, расстояния, проекции), в графовом пространстве ситуация противоположная.
Компоненты элемента (потенциалы и токи в узлах) материальны, а положение элемента в пространстве просто виртуально и определяется набором значений компонентов.
Построение системы координат на графике
Постановка задачи
Задачу построения системы координат (СК) на графе можно сформулировать следующим образом.
- Граф представляет собой набор связанных между собой вершин.
- Из множества всех вершин графа мы выделили основа — множество вершин, для которых можно построить метрический тензор — расстояние или лапласиан.
- Остальные вершины графа являются внешними.
Для внешних вершин известны:
- Полная связность вершины (сумма весов ее связей).
- Связи между вершинами.
- Соединения между внешними вершинами и базовыми вершинами.
- Полная связность вершины (сумма весов ее связей).
Система координат должна позволять определять расстояния между всеми (любыми) вершинами графа.
Уточним, что дана только одна из возможных постановок задачи построения системы.
Комбинации известных параметров и параметров, подлежащих определению, могут различаться.
Базовый подграф
Обозначим множество базовых вершин графа индексом(якорь), а набор остальных вершин индексируется
.
Объединение этих множеств дает все вершины графа.
Мы считаем, что узлы графа связаны с остальными хотя бы одной связью.
График общего метрического тензора расстояний (DMT)
можно разделить на 4 матрицы:
– тензор метрики расстояний подграфа;
— матрица дикоординат внешних вершин
в основе
.
В данной матрице координаты вершины являются столбцом матрицы, в транспонированной
- линия.
представляет собой матрицу скалярных произведений вершин графа, не входящих в базис.
По условиям задачи известен только Грамиан подграфа
.
Матрицы
И
— это то, что необходимо определить на основе данных о структуре графа.
Структура лапласиана
Аналогичным образом (на 4 подматрицы) можно разбить лапласиан графа.
В отличие от Грамиана, лапласиан графа здесь минорный — данные об ортоцентре графа отсутствуют.
— матрица связей (смежности) между внешними вершинами графа
и его основа
.
— малый лапласиан, соединения внешних вершин.
На диагонали этой матрицы находятся значения полной проводимости узла (суммарный вес его ребер), остальные элементы — значения связи между узлами.
Эта матрица обычно обратима.
Ее обращение называется фундаментальная матрица :
Термин «фундаментальный» взят из теории цепей Маркова с поглощением.
В таких цепях роль базовых играют узлы, из которых нет возврата (поглощающие).
Пример использования этой матрицы приведен в статья о методе ранжирования предметы по степени их удаленности от заданных.
Предполагается, что одна из матриц (минорный лапласиан
или фундаментальная матрица
) известны.
Согласно (4.2) одно можно выразить из другого.
Основные идентичности
Грамиан и Лапласиан графа взаимно обратны.
Чтобы найти тождества, связывающие приведенные выше матрицы, необходимо подставить блочные матрицы (4.1.1) и (4.1.2) в (4.3) (предварительно лапласиан должен быть ограничен условными параметрами ортоцентра).
В результате получаем следующие соотношения.
Лапласова связь
и удаленно
метрические тензоры базиса подграфа:
(4.4.1) позволяет вычислить один тензор на основе другого.
Если базис задан в виде связей, то для определения лапласиана базиса
можно использовать следующее удостоверение:
Здесь
является минорным исходного лапласиана по базисным вершинам.
— Лапласиан, подматрица базиса LMT. На основе этого лапласиана мы можем найти грамиан подграфа
.
Если известна матрица связей между внешними узлами графа и его базисом
, а также фундаментальная матрица
, то мы сможем вычислить барицентрические координаты узлов:
Барицентрическая координатная матрица
также называемый матрица влияния .
Действительно, его значения отражают влияние базовых вершин на остальные (в задаче Дирихле влияние значений граничных узлов на внешние).
Би- и дикоординаты узлов взаимны.
Выражается через тензор метрического базиса:
Дикоординаты включают в себя единицы и значения скалярных произведений элементов с базисом:
.
Бикоординаты состоят из скалярной составляющей (орбитальной) и барицентрических координат:
Если известны определители фундаментальной матрицы и базиса LMT, то можно вычислить общий скалярный потенциал лапласиана графа:
Матрица скалярных произведений внешних вершин
в подграфовом базисе
представляет собой билинейную форму, выраженную через би- или дикоординаты вершин:
Фундаментальная матрица и расстояния между вершинами
Очевидно, что значения матрицыв общем случае будет отличаться от значений скалярных произведений вершин исходного графа
.
Разница между ними выражается фундаментальной матрицей:
Формулу (4.5) можно использовать для вычисления истинного скалярного произведения между вершинами (элементами)
, если известно скалярное произведение элементов базиса подграфа
и фундаментальная матрица
.
В исходном графе нормы вершин равны нулю.
Соответственно, скалярное произведение
можно выразить через квадрат расстояния между вершинами
:
.
Тогда (4.5) можно представить в виде:
Мы уже встречались с этим выражением во второй части при определении скалярного произведения элементов — (2.6) .
Сравнивая выражения, видим, что значения фундаментальной матрицы можно выразить через скалярное произведение вершин относительно базиса:
Штрихи обозначают проекции вершин на базовое пространство.
скалярное произведение пар
И
.
Через
обозначает скалярное произведение нормалей вершин
в космос
.

Нормаль задается как направление от элемента к его проекции в базисном пространстве.
Это близко к определению скалярного произведения координат элементов в обычных системах координат (на векторной основе), только вместо начала координат здесь указывается пробел.
Если какая-либо из вершин принадлежит базисному пространству, то ее скалярное произведение по базису с любой другой вершиной равно нулю.
Таким образом, если один из элементов фундаментальной матрицы равен нулю, то вся строка и столбец матрицы также будут равны нулю.
Если элементы
И
совпадают, то значение фундаментальной матрицы равно расстоянию от элемента до базового пространства или, согласно (2.5), отрицательной норме элемента:
— значения диагональных элементов фундаментальной матрицы.
Расстояния между элементами вне базисного пространства
Если вершины не принадлежат базовому пространству (принадлежат суперпространству), то возможны две ситуации: 1. Вершины принадлежат одному и тому же (над)пространству.В этом случае вершины и их проекции на базовое пространство лежат в одной плоскости.
2. Вершины принадлежат разным (над)пространствам (показано на рисунке выше).
В первой ситуации направление нормалей
И
коллинеарно, поэтому скалярное произведение совпадает с произведением расстояний от вершин до базового пространства:
Знак квадратного корня положителен, если вершины находятся на одной стороне пространства (нормали указывают в одном направлении), и отрицателен в противном случае.
Эта формула уже была приведена в 2-я статья из серии - (2.7) .
Формула (4.6.3) описывает частный (хотя и важный) случай.
Орбитальная матрица
Для построения системы координат необходимо определить скалярную составляющую бикоординат – то, что называется орбиталь элемента .Без этого компонента расстояния на графике можно получить только в пределах базового пространства.
Об определении бикоординаты была получена формула, связывающая орбиталь элемента и ее проекцию на базисное пространство с нормой элемента - (2.9.1):
Проекционную орбиталь элемента можно вычислить с помощью билинейной формы (2.9.2), поскольку мы знаем, как базисный грамиан
, и барицентрические координаты элементов (4.4.3).
Значения норм элементов согласно (4.6.2) можно брать из диагональных элементов фундаментальной матрицы.
Сложив все вместе, получим выражение для матрицы взаимных орбиталей:
Диагональные значения данной матрицы
являются орбиталями вершин.
Таким образом определяются бикоординаты внешних вершин.
На основе бикоординат можно рассчитать дикоординаты по формуле (4.4.4) и получить матрицу взаимных норм (4.4.2).
Задача построения системы координат выполнена.
Пример построения системы координат
Граф из 6 вершин с базисом 3
Обратимся к графику, представленному на CDPV. На нем выделены три базовые вершины – 1, 2 и 5. Требуется определить координаты остальных внешних вершин – 3, 4 и 6. Вершины базиса могли быть любыми, в том числе не связанными друг с другом.Хорошей основой являются вершины с наибольшей связностью (в нашем графе это вершины 2, 4, 5).
При таком базисе остальные вершины слабо связаны друг с другом.
Минор лапласиана и фундаментальная матрица диагональны (связей нет) и все упрощается.
Но нас интересует общий случай, когда между внешними вершинами имеются связи.
Исходный график для проверки
Лапласиан: \begin{array}{c | c c c c c c} Л&1&2&3&4&5&6\\ \hline 1 & 2 & -1 & 0 & 0 & -1 & 0 \\ 2 & -1 & 3 & -1 & 0 & -1 & 0 \\ 3 & 0 & -1 & 2 & -1 & 0 & 0 \\ 4 & 0 & 0 & -1 & 3 & -1 & -1 \\ 5 & -1 & -1 & 0 & -1 & 3 & 0 \\ 6 & 0 & 0 & 0 & -1 & 0 & 1 \\ \конец{массив} Соответствующая матрица расстояний: \begin{array}{c | c c c c c c} Вопрос & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 1 & 0 & 0.(63) & 1.(18) & 1.(18) & 0.(63) & 2.(18) \\ 2 & 0.(63) & 0 & 0.(72) & 0.(90) & 0.(54) & 1.(90) \\ 3 & 1.(18) & 0.(72) & 0 & 0.(72) & 0.909 & 1.(72) \\ 4 & 1.(18) & 0.(90) & 0.(72) & 0 & 0.(72) & 1.00 \\ 5 & 0.(63) & 0.(54) & 0.(90) & 0.(72) & 0 & 1.(72) \\ 6 & 2.(18) & 1.(90) & 1.(72) & 1.00 & 1.(72) & 0 \\ \конец{массив}Входные данные
Грамиан (дистанционный метрический тензор) базисабудет иметь вид (данные взяты из общей матрицы расстояний графа и разделены на -2): \begin{array}{c | с с с с} Gm_{aa} & 0 & 1 & 2 & 5 \\ \hline 0 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & -0.3(18) & -0.3(18) \\ 2 & 1 & -0.3(18) & 0 & -0.(27) \\ 5 & 1 & -0.3(18) & -0.(27) & 0 \\ \конец{массив} Матрица смежности (связи с базисом)
в нашем примере это выглядит так: \begin{array}{c | с с с} C^{at} & 3 & 4 & 6 \\ \hline 1 & 0 & 0 & 0 \\ 2 & 1 & 0 & 0 \\ 5 & 0 & 1 & 0 \\ \конец{массив} Мы видим, что 3-я вершина соединена со 2-й вершиной базиса, а 4-я — с 5-й.
6-я вершина не соединена с основанием.
Минор лапласиана внешних связей
будет так:
\begin{array}{c | с с с}
L^{tt} & 3 & 4 & 6 \\
\hline
3 & 2 & -1 & 0 \\
4 & -1 & 3 & -1 \\
6 & 0 & -1 & 1 \\
\конец{массив}
Оригинальная триада
- спросил.
На основе этих матриц можно восстановить все параметры исходного графа.
Восстановление графика
Инвертирование младшего лапласиана, получаем значения фундаментальной матрицы
(4.2): \begin{array}{c | с с с} F_{tt} & 3 & 4 & 6 \\ \hline 3 & 2/3 & 1/3 & 1/3 \\ 4 & 1/3 & 2/3 & 2/3 \\ 6 & 1/3 & 2/3 & 5/3 \\ \конец{массив} Барицентрические координаты внешних вершин
получим из формулы (4.4.3): \begin{array}{c | с с с} B^{a}_{t} & 3 & 4 & 6 \\ \hline 1 & 0 & 0 & 0 \\ 2 & 2/3 & 1/3 & 1/3 \\ 5 & 1/3 & 2/3 & 2/3 \\ \конец{массив} Мы видим, что барицентрические координаты вершины 6 совпадают с барицентрическими координатами узла 4. Это характерно для всех узлов, связанных только с одной вершиной.
Геометрически это означает, что проекции узлов 6 и 4 на базисное пространство совпадают. Во всех вершинах компонента базовой вершины 1 равна нулю.
То есть только те вершины, которые с ними связаны — внешние вершины базового подграфа — вносят вклад в барицентрические координаты вершин графа.
Обратная орбитальная матрица
рассчитывается на основе барицентрических координат и фундаментальной матрицы (4.8):
\begin{array}{c | с с с}
W_{tt} & 3 & 4 & 6 \\
\hline
3 & 0.(54) & 0.(18) & 0.(18) \\
4 & 0.(18) & 0.(54) & 0.(54) \\
6 & 0.(18) & 0.(54) & 1.(54) \\
\конец{массив}
Теперь вы можете построить бикоординаты элементов.
— скалярная составляющая равна диагональным значениям орбитальной матрицы, делённым на (-2):
\begin{array}{c | с с с}
Bm^{a}_{t} & 3 & 4 & 6 \\
\hline
0 & -0.(27) & -0.(27) & -0.7(72) \\
1 & 0 & 0 & 0 \\
2 & 0.(6) & 0.(3) & 0.(3) \\
5 & 0.(3) & 0.(6) & 0.(6) \\
\конец{массив}
Умножив матрицу бикоординат на грамиан базиса, получим бикоординаты
.
\begin{array}{c | с с с}
Dm_{at} & 3 & 4 & 6 \\
\hline
0 & 1 & 1 & 1 \\
1 & -0.5(90) & -0.5(90) & -1.(09) \\
2 & -0.(36) & -0.(45) & -0.9(54) \\
5 & -0.(45) & -0.(36) & -0.8(63) \\
\конец{массив}
Расстояние между вершинами 6 и 1 графа согласно этой матрице должно быть равно
.
Глядя на общую матрицу расстояний, можно увидеть, что это так.
Матрица скалярных произведений в подграфе
является произведением взаимных координат вершин:
\begin{array}{c | с с с}
N_{tt} & 3 & 4 & 6 \\
\hline
3 & -0.(6) & -0.(69) & -1.1(96) \\
4 & -0.(69) & -0.(6) & -1.1(6) \\
6 & -1.1(96) & -1.1(6) & -1.(6) \\
\конец{массив}
Согласно этой матрице все внешние вершины графа лежат вне базового пространства (нормы ненулевые).
Осталось определить расстояния между внешними вершинами
.
Мы используем (4,5'):
\begin{array}{c | с с с}
Q_{tt} & 3 & 4 & 6 \\
\hline
3 & 0 & 0.(72) & 1.(72) \\
4 & 0.(72) & 0 & 1.0 \\
6 & 1.(72) & 1.0 & 0 \\
\конец{массив}
Сравните с исходной матрицей расстояний
и убедиться, что все значения совпадают
Теги: #граф #лапласиан #матрица смежности #координаты расстояний #барицентрические координаты #фундаментальная матрица #скалярное произведение #математика

-
Бэби-Бумеры… Что Мы Будем С Ними Делать?
19 Oct, 24 -
От Аутсорсинга К Разработке (Часть 1)
19 Oct, 24 -
Мегатонны Макулатуры Одним Движением Руки
19 Oct, 24


