От статьи об одномерных мирах вы знаете, что одномерным мир делает то, что положение в нем определяется одной единицей информации.
Оно также должно быть непрерывным (или близким к непрерывному с практической точки зрения).
Я описал несколько примеров измерений: бесконечную линию дохода, представленную бесконечной прямой линией; линия радуги, конечная, с ограничивающими стенками, представленными отрезком; эолова линия направлений ветра, конечно периодическая, изображаемая отрезком, левый конец которого совпадает с правым, или, что то же самое, кругом.
Я вскользь упомянул еще один пример — о мире, бесконечном в одну сторону и конечном в другую.
В еще одна статья Я подчеркнул, что существует множество видов измерений, но физические измерения пространства обладают уникальными и особыми (и к тому же весьма очевидными) свойствами, отличающими их от других видов измерений.
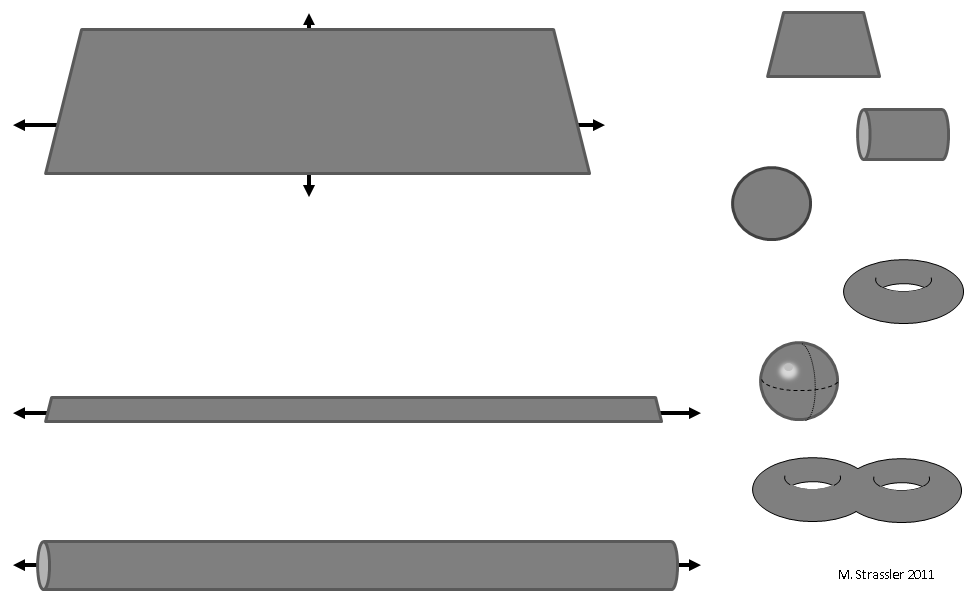
Рис.
1: двумерные миры А как насчет двумерных миров? Неудивительно, что типов двумерных миров гораздо больше, чем типов одномерных миров.
Несколько примеров таких пространств показаны на рис.
1. Можно представить себе мир, бесконечный в обоих направлениях: плоскость (слева вверху).
Можно представить себе мир, который бесконечен в одном направлении и образует либо сегмент, либо круг в другом.
Такие миры естественно называть полосой и трубкой (слева внизу).
Можно представить конечный мир в обоих направлениях (правая часть рис.
1).
А сколько возможностей! Только на этой картинке сверху вниз видны квадрат, цилиндр (круглая часть банки без крышек и внутренностей), диск, тор (что-то вроде автомобильной шины), сфера (только поверхность), двойная шина.
И это не все варианты.
Если экстраполировать в будущее, то станет ясно, что к тому времени, когда мы доберемся до трех измерений и пойдем дальше, мы уже не сможем составлять подобные списки.
Как и в одномерных пространствах, положение в двумерном пространстве определяется двумя частями информации.
Примером сферы (в хорошем приближении) может быть поверхность Земли: любое место может быть обозначено широтой и долготой.
Муравей, идущий по садовому шлангу, движется по плоской трубе и в любой момент времени находится на определенном расстоянии от крана и под определенным углом к вертикали.
Многополосное шоссе — это, по сути, двумерная полоса с очень длинной и короткой стороной: две части информации, необходимые для определения вашего положения, — это расстояние от начала дороги и расстояние от ее правого края.
Давайте вспомним линию доходов.
«Ваш доход за последний год — это определенное число в вашей местной валюте.
Оно может быть положительным или отрицательным, большим или маленьким; ее можно представить в виде точки на линии, как на рис.
1, которую мы назовем «точкой дохода».
Каждая точка на линии представляет собой возможный доход».
Если вы состоите в браке и у вас и у вашего супруга есть доход, два денежных потока, поступающих в ваше домохозяйство, можно представить в виде плоскости с двумя доходами.
Два числа, которые описывают точку на этой плоскости.
будет ваш доход и доход вашего супруга.
Вот умный пример тора, показывающий, как можно представить интересные двумерные формы, размеры которых не совпадают с размерами физического пространства.
На рис.
3 статьи об одномерных мирах мы увидели, что возможные направления ветра образуют одномерный мир в виде круга (или линии, начало и конец которой совпадают).
Возможные направления движения парусника также образуют аналогичный круг.
Но любой, кто плавал, знает, что не обязательно идти в том же направлении, что и ветер; если поставить парус под углом, то можно плыть на запад, даже если ветер дует с севера.
Итак, если я запрошу две части информации — в каком направлении дует ветер и в каком направлении движется моя парусная лодка — они оба будут точками на круге.
Две части информации, расположенные по кругу, представляют точку на торе.
Прежде чем продолжить, позвольте мне упомянуть о естественной и распространенной путанице.
Я уже намекал на это в приведенных выше описаниях различных миров.
Не путайте размеры самих фигур с определенным способом представления этих размеров или форм! Свойство круга состоит в том, что если вы двинетесь по нему в любом направлении, вы вернетесь туда, откуда начали.
У круга нет ничего ни внутри, ни снаружи.
Простое представление круга как замкнутой кривой на двумерной плоскости создаст впечатление, будто у него есть внутренняя и внешняя стороны.
Но это просто свойство изображения круга на плоскости, а не свойство самого круга.
Теги: #физика #Мэтт Страсслер #Мэтт Страсслер #Мэтт Страсслер #дополнительные измерения #измерения космоса #двумерные миры

-
Аварийное Восстановление Как Услуга
19 Oct, 24 -
Мобильный Для Интернета
19 Oct, 24 -
Почему Мы Выбрали Lexus Rx450H
19 Oct, 24 -
Как Не Умереть На Проекте Или 5 Лайфхаков
19 Oct, 24


