ТЛ;ДР
- В глубоких нейронных сетях основным препятствием для обучения являются седловые точки, а не локальные минимумы, как считалось ранее.
- Большинство локальных минимумов целевой функции сосредоточено в относительно небольшом подпространстве весов.
Сети, соответствующие этим минимумам, дают примерно одинаковые потери на тестовом наборе данных.
- Сложность ландшафта возрастает по мере приближения к глобальным минимумам.
Практически во всем объеме пространства весов подавляющее большинство седловых точек имеют большое количество направлений, по которым от них можно уйти.
Чем ближе к центру кластера минимумов, тем меньше «направлений ухода» для седловых точек, встречающихся на этом пути.
- Пока неясно, как найти глобальный экстремум (любой из них) в подпространстве минимумов.
Похоже, это очень сложно; и не факт, что типичный глобальный минимум намного лучше типичного локального, как по потерям, так и по способности к обобщению.
- В кластерах минимумов имеются специальные кривые, соединяющие локальные минимумы.
Функция потерь на этих кривых принимает лишь несколько большие значения, чем в самих экстремумах.
- Некоторые исследователи считают, что широкие минимумы (с большим радиусом «дыры» вокруг) лучше узких.
Но есть также немало учёных, которые считают, что связь между шириной минимума и обобщающей способностью сети очень слабая.
- Пропускные соединения делают местность более удобной для градиентного спуска.
Кажется, вообще нет причин Нет использовать остаточное обучение.
- Чем шире слои в сети и чем их меньше (до определенного предела), тем более гладкий ландшафт целевой функции.
К сожалению, чем более избыточна параметризация сети, тем более восприимчива нейронная сеть к переобучению.
Если вы используете сверхширокие слои, легко найти глобальный минимум в наборе обучающих данных, но такая сеть не будет обобщать.
Я даже КДПВ ставить не буду.
Статья состоит из трёх частей: обзор теоретических работ, обзор научных работ с экспериментами и перекрестное сравнение.
Первая часть немного суховата, если надоест, переходите сразу к третьей.
Но сначала пояснение по поводу второго пункта.
Объявленное подпространство имеет небольшой общий объем, но может быть сколь угодно большим по размеру при проецировании на любую прямую линию в гиперпространстве.
Он содержит как скопления минимумов, так и просто области, где функция потерь мала.
Представьте себе два последовательных линейных нейрона.
Выход из сети будет
.
Допустим, мы хотим научить их воспроизводить функцию тождества.
.
Если мы применим потери L2 к сети, поверхность функции ошибки будет выглядеть так:
: 
Где по оси абсцисс отложено
, а по ординате -
.
Это очевидно, что
идеально воспроизводят функцию идентичности, но они также делают то же самое
и, например,
.
Все это глобальные минимумы (их бесконечное количество), а красно-бордовая область на графиках — это подпространство минимумов (как видите, оно простирается бесконечно вдоль обеих осей, но по мере удаления становится все тоньше с нуля).
Мы наблюдаем такое поведение из-за симметрии весов, и это явление не уникально для линейных сетей.
Частично это можно исправить регуляризацией, но даже в этом случае остаются два глобальных минимума.
И
(плюс-минус искажение от регуляризации).
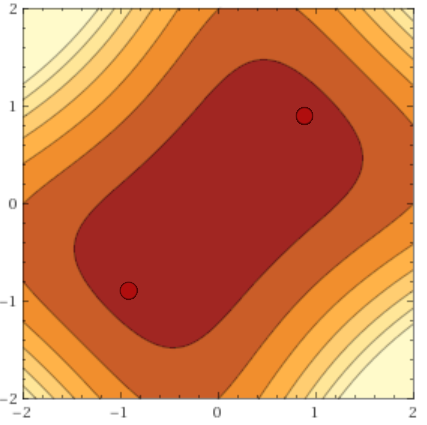
В дальнейшем под «глобальным минимумом» я буду понимать «любой из одинаковых глобальных минимумов», а под «кластером минимумов» — «любой из симметричных кластеров локальных минимумов».
Обзор теоретических работ
Как известно, обучение нейронной сети – это поиск минимальной целевой функции потерь.
в пространстве весов
.
К сожалению, поиск глобального минимума произвольной дифференцируемой функции относится к классу NP-трудных задач[1].
Кроме того, нейронные сети могут иметь очень разную архитектуру и принимать на вход любые данные, поэтому надежды на глубокий анализ одной формулы с четко обозначенными ограничениями нет. Функция
невероятно многомерен, поэтому применять здесь метод перебора тоже нетривиально.
Однако даже некоторые общие факты о типичном пейзаже
может принести немалую пользу: по крайней мере, задать общее направление практическим исследованиям.
До недавнего времени желающих взяться за такую титаническую задачу было немного, но в начале 2014 года вышла статья Эндрю Сакса и других [2], в которой обсуждаются нелинейный динамика обучения линейный нейронные сети (приведена формула оптимальной скорости обучения) и лучший способ их инициализации (ортогональные матрицы).
Авторы получают интересные идеи из SVD-разложения произведения весов сети и выдвигают теорию, как результаты могут быть перенесены в нелинейные сети.
Хотя работа Сакса не имеет прямого отношения к теме этой статьи, она побудила других исследователей глубже изучить динамику обучения нейронных сетей.
В частности, чуть позже, в 2014 году, Ян Дофин и его команда[3] проанализировали существующую литературу по динамике обучения и обратили внимание не только на статью Сакса, но и на работу Брея и Дина[4] 2007 года по статистике критические точки в случайных гауссовских полях.
Они предлагают модификацию метода Ньютона (Saddle Free Newton, SFN), которая не только лучше уходит от седловых точек, но и не требует вычисления полного гауссиана (минимизация происходит по векторам так называемого подпространства Крылова).
В статье показаны очень красивые графики повышения точности сети, а это значит, что SFN что-то делает правильно.
Работа Дофина, в свою очередь, дает толчок новым исследованиям распределения критических точек в пространстве весов.
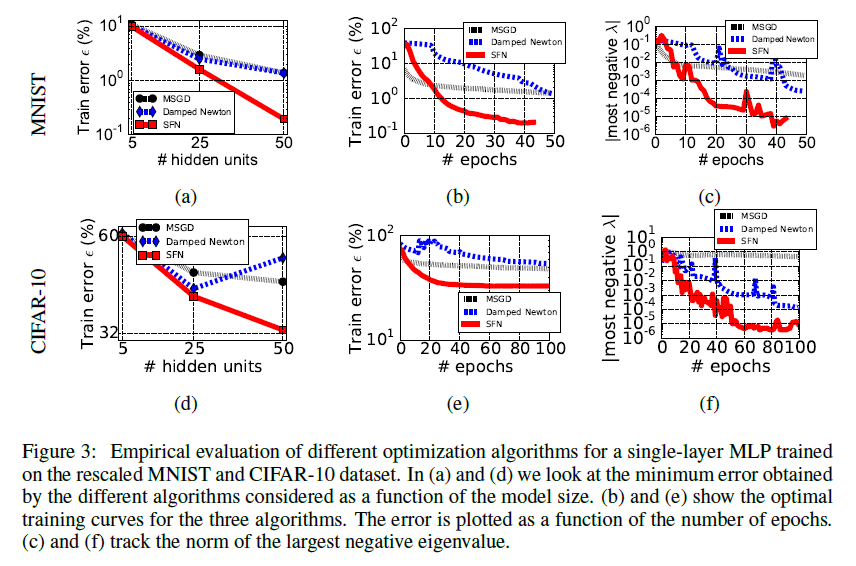
Итак, существует несколько направлений анализа заявленной проблемы.
Первый — украсть у кого-то проверенную математику и применить ее к своей собственной модели.
Этот подход с невероятным успехом был использован Анной Хроманской и командой[5][6], используя уравнения теории спиновых стекол.
Они ограничились рассмотрением нейронных сетей со следующими характеристиками:
- Сети прямых продаж.
- Глубокие сети.
Чем больше весов, тем лучше работают асимптотические приближения.
- Функции активации ReLU.
- L2 или функция потери шарнира.
- Вероятность активности конкретного нейрона описывается распределением Бернулли.
- Пути активации (какой нейрон активирует) распределены равномерно.
- Количество весов избыточно для формирования функции распределения
.Не существует весов, удаление которых блокирует обучение или прогнозирование.
- Сферический предел веса:
(Где
— количество весов в сети) - Все входные переменные имеют нормальное распределение с одинаковой дисперсией.
- Пути активации в нейронной сети не зависят от конкретного
. - Входные переменные независимы друг от друга.
- Минимумы функции потерь в нейронной сети образуют кластер в относительно небольшом подпространстве весов.
За определенным пределом значения функции потерь их количество начинает экспоненциально уменьшаться.
- Для правильно обученных глубоких нейронных сетей большинство локальных минимумов примерно одинаковы по производительности на тестовом наборе.
- Вероятность попадания в «плохой» локальный минимум заметна при работе с небольшими сетями и экспоненциально уменьшается с увеличением количества параметров в сети.
- Позволять
— число отрицательных собственных значений гессиана в седловой точке.Чем он больше, тем больше путей, по которым градиентный спуск может уйти от критической точки.
Для каждого
есть некий показатель значения целевой функции
, начиная с которого плотность седловых точек с такими
начинает экспоненциально уменьшаться.Эти цифры строго увеличиваются.
По-русски это означает, что функция потерь имеет слоистую структуру, и чем ближе мы будем к глобальному минимуму, тем больше будет неприятных седловых точек, из которых сложно выбраться.
Если что и может открыть пресловутый «черный ящик» нейронных сетей, так это математика из квантовой физики.
Но есть и очевидный недостаток: очень прочные помещения.
Даже 1 и 2 из группы реалистичных мне кажутся сомнительными, не говоря уже о группе нереалистичных.
Самым серьезным ограничением модели мне кажется равномерное распределение путей активации.
Что, если какая-то небольшая группа путей активации отвечает за классификацию 95% элементов набора данных? Получается, что он образует как бы сеть внутри сети, что существенно снижает эффективную эффективность.
.
Есть еще одна загвоздка: утверждения Хромански трудно фальсифицировать.
Не так уж сложно построить пример весов, представляющих «плохой» локальный минимум [7], но это, похоже, не противоречит посылу статьи: их утверждения должны быть справедливы для больших сетей.
Однако даже предоставленный набор весов для умеренно глубокой сети прямого распространения, которая плохо классифицирует, скажем, MNIST, вряд ли станет сильным доказательством, поскольку авторы утверждают, что вероятность встретить «плохой» локальный минимум имеет тенденцию к нулю, а не то, чтобы их вообще не было.
Плюс «для правильно обученных глубоких нейронных сетей» — довольно расплывчатое понятие… 
Второй подход предполагает построение модели простейшей возможной нейронной сети и итеративное доведение ее до состояния, в котором она сможет описывать современных монстров машинного обучения.
У нас уже давно есть базовая модель – это линейный нейронные сети (т.е.
сети с функцией активации
) с одним скрытым слоем.
Они хорошо поддаются анализу и изучаются уже давно, однако результаты этих теоретических исследований мало кого интересовали, так как в целом линейные сети не очень полезны.
По крайней мере, до недавнего времени они мало кого интересовали.
Используя довольно слабые ограничения на размер слоев и свойства данных, Кенджи Кавагути[8] развивает результаты работы [9] 1989 года и показывает, что в некоторых случаях линейный нейронные сети с L2-потерей
- Хотя
невыпуклый и невогнутый - Все локальные минимумы глобальны (их может быть больше одного)
- А все остальные критические точки являются седловыми точками.
- Если
— седловая точка функции потерь и ранг матричного произведения весов сети равен рангу самого узкого слоя нейронной сети, тогда гессиан в
имеет хотя бы одно строго отрицательное собственное значение.
Сравните с функциями
на нуле и
В
.
После этого Кавагути принимает во внимание сети с активацией ReLu, немного ослабляет ограничения Чороманской [6] и доказывает те же утверждения для нейронных сетей с нелинейностями ReLu и потерями L2. (В следующей статье [10] тот же автор дает более простое доказательство).
Хардт и Ма[11], вдохновленные результатами работы [8] и успехом остаточного обучения, доказывают еще более сильные утверждения в пользу линейный сети с пропущенными связями: при определенных условиях у них даже нет «плохих» критических точек без отрицательных собственных значений гессиана (теоретическое обоснование того, почему «короткие замыкания» в сети улучшают ландшафт, см.
в [12]), и [ 13] например графики
до и после добавления пропущенных соединений).
Накопленная база знаний обобщена совсем недавно опубликованной работой Юна, Сра и Джадбабайе [14].
Авторы усиливают теоремы Кавагути и, подобно Хроманске, разделяют пространство весов.
линейный нейронную сеть на подпространство, содержащее только седловые точки, и подпространство, содержащее только глобальные минимумы (приведены необходимые и достаточные условия).
Более того, ученые наконец-то делают шаг в интересующем нас направлении и доказывают аналогичные утверждения для нелинейных нейронных сетей.
Пусть последнее будет сделано при очень сильных предпосылках, но это предпосылки отличный из условий Хромански.
Обзор работ с визуализацией
Третий подход заключается в анализе значений Гессе в процессе обучения.Математикам давно известны методы оптимизации второго порядка.
Люди, занимающиеся машинным обучением, время от времени с ними заигрывают (методами, а не математиками.
хотя и математиками тоже), но даже усеченные алгоритмы спуска второго порядка никогда не пользовались особой популярностью.
Основная причина этого кроется в стоимости расчета необходимых для спуска данных с учетом второй производной.
Честно рассчитанный гессиан берет квадрат количества весов памяти: если в сети миллион параметров, то они будут содержаться в матрице вторых производных.
.
Но еще я хочу как-то вычислить собственные значения этой матрицы.
По этой же причине мало работ, позволяющих посмотреть на динамику изменения гессиана в процессе обучения.
Точнее, я нашел ровно одну работу Янна ЛеКуна и компании [34], посвященную именно этому, да и то они работают с относительно примитивной сетью.
Плюс в [3] и [12] есть пара соответствующих комментариев и графиков.
ЛеКун[34]: На протяжении всего обучения гессиан почти полностью состоит из нулевых значений.
Во время оптимизации гистограмма Гессиана дополнительно сжимается до нуля.
Ненулевые значения распределены неравномерно: длинный хвост отброшен в положительном направлении, а отрицательные значения сосредоточены вокруг нуля.
Часто нам только кажется, что обучение остановилось, когда мы просто находимся в бассейне с небольшими уклонами.
В точке останова имеются отрицательные собственные значения гессиана.

Чем сложнее данные, тем более удлинён положительный хвост распределения собственных значений.
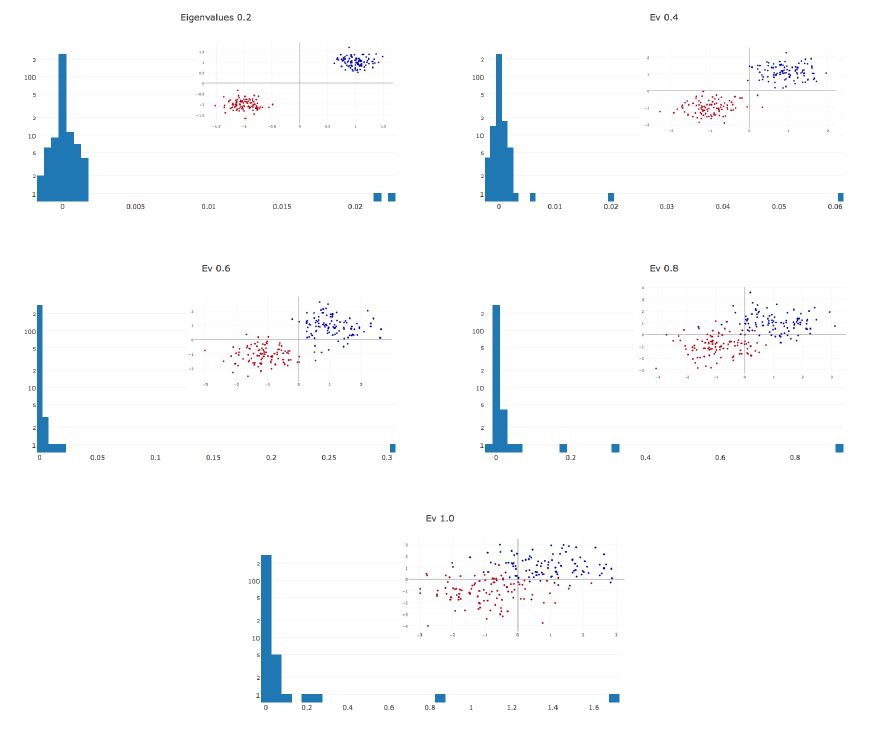
Чем больше параметров в сети, тем больше гистограмма собственных значений растягивается в обоих направлениях.

Дофин и др.
[3]: На графиках A и C ось
относительная часть отрицательных значений откладывается в критическую точку, в которой обучение остановилось, согласно
ошибка задерживалась на обучающем наборе.
На графиках B и D показаны гистограммы собственных значений матрицы второй производной для трех точек из графиков A и C соответственно.
Обратите внимание, что они согласуются с гистограммами ЛеКуна.
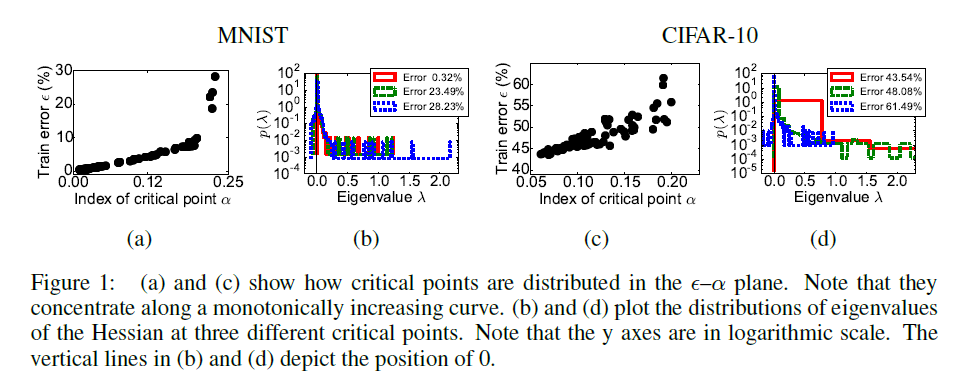
Отчетливо видна корреляция между количеством направлений выхода из седловой точки и качеством работы сети в ней.
Орхан и Питков[12]: показывает относительное количество вырожденных и отрицательных собственных значений гессиана.
В статье говорится не совсем о том же, что в [3] и [34], но в целом графики косвенно подтверждают результаты двух предыдущих работ. 
Четвертый способ – непосредственный анализ ландшафта.
с использованием визуализаций любых проекций.
Идея тривиальна, но, как уже говорилось, ее совсем непросто реализовать, поскольку в
масштабов могут быть миллионы.
Обычно рассматривают два типа визуализаций: значения функции потерь при изменении
в пространстве весов вдоль любой кривой и график функции потерь в окрестности любой точки
, Где
И
— некоторые векторы, определяющие плоскость сечения пространства весов.
В случае одномерной проекции обычно визуализируются переходы от начального состояния сети к конечному (непосредственно или по кривой обучения) или между двумя конечными состояниями; в двумерном состоянии они обычно берут два наиболее значимых вектора в PCA-разложении последнего участка кривой обучения.
Помимо многомерности, проблема визуализации целевой функции осложняется тем, что по существу одинаковые минимумы могут иметь очень разные веса.
Например, если в линейной нейронной сети веса в одном слое уменьшаются на
один раз, а в следующий раз – через
раз результирующие наборы весов и области пространства вокруг них будут сильно различаться, в то время как изученные функции будут по существу одинаковыми.
Дополнительным измерением для анализа является тип минимизатора или параметры конкретного типа минимизатора, с помощью которого были получены данные.
.
Одной из таких работ является [16].
В нем исследователи рассматривают интервал между конечными точками запусков SGD, Adam, Adadelta и RMSProp. Как и во многих других работах, обнаружено, что разные алгоритмы находят характерно разные минимумы.
Авторы статьи также показывают, что если в процессе обучения изменить тип алгоритма, то
изменит курс на другой минимум.
В качестве второго бонуса исследователи смотрят, как пакетная нормализация повлияет на ландшафт между конечными точками, и приходят к выводу, что, во-первых, при пакетной нормализации качество результирующего минимума гораздо меньше зависит от точки инициализации, а во-вторых, между конечными точками.
На ландшафте целевой функции появляются «стены» — узкие области с очень большим значением
(непонятно откуда это и что с этим делать).
В любом случае на приведенных выше графиках между минимумами видны «холмы» потерь, а не какая-то сложная поверхность.

Сейчас нас больше интересует группа исследований, доказывающих, что между двумя минимумами в пространстве весов
И
Практически всегда можно провести некоторую кривую, на всей длине которой функция потерь не будет превышать
Для
, отделенный от нуля некоторой границей, но значительно меньший, чем типичные значения функции потерь [17][18][19].
Существует несколько способов формирования такой кривой: как правило, они предполагают простой отрезок между
И
разбивается на звенья, после чего соединяющие их узлы перемещаются градиентным спуском в пространстве весов.
Используя такие кривые, можно, например, собирать более качественные ансамбли сетей [18].
Их результаты показывают, что кластер минимумов имеет «пористую» структуру.
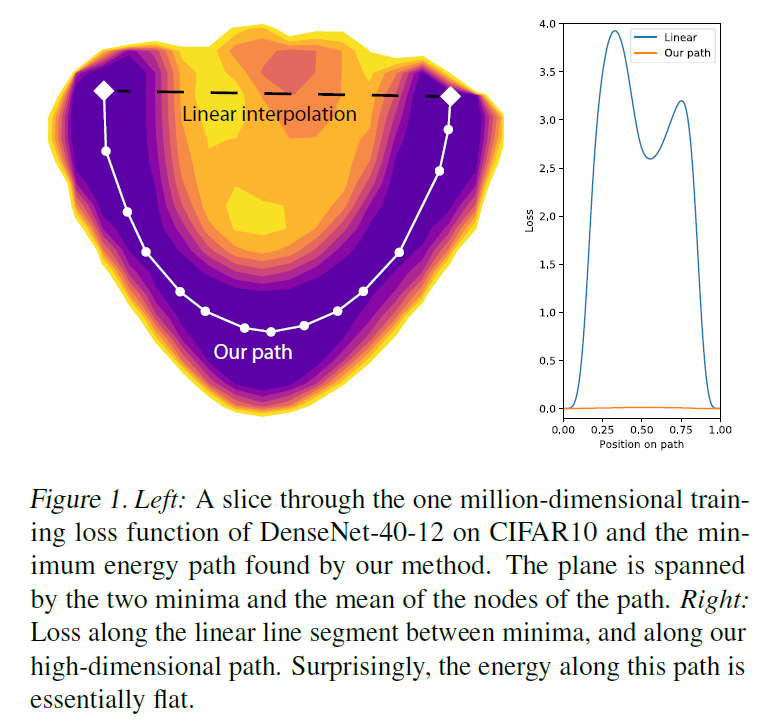
В том же духе находится совсем недавняя статья международной группы учёных[23], в которой они строят графики потерь между
И
и угол между направлениями градиента в моменты времени
И
.
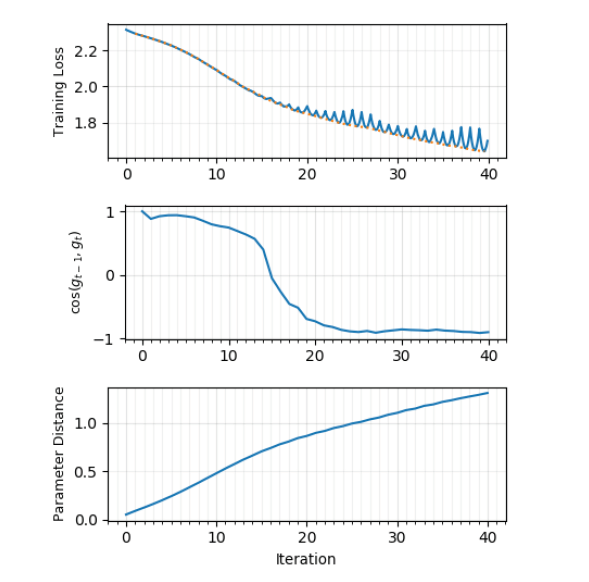
Получается, что в начале обучения градиенты соседних шагов направлены примерно в одну и ту же сторону и функция ошибки монотонно убывает, но с определенного момента времени
между
И
начинает демонстрировать характерные минимумы, а угол между градиентами стремится к ~170 градусам.
Действительно похоже, что градиентный спуск «отскакивает» от стенок «седла» с небольшим наклоном! Картина становится намного яснее, когда градиентный спуск выполняется с использованием всего набора данных; использование минибатча искажает картину до неузнаваемости, что логично.
Скорость обучения не влияет на график углов, но влияет размер пакета.
Исследователи не обнаружили пересечения локальных минимумов.
До сих пор мы считали, что качество найденного минимума зависит только от его глубины.
Однако многие исследователи отмечают, что ширина минимума также имеет значение.
Формально это можно определить по-разному; Я не буду приводить различные формулировки (см.
[20], если вы их еще хотите увидеть), здесь достаточно понять основную идею.
Вот иллюстрация: 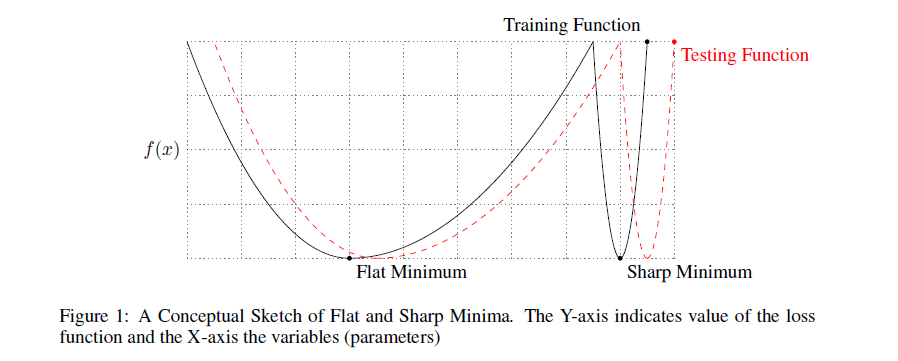
Минимум черного графика слева широкий, справа узкий.
Почему это имеет значение? Распределение обучающих данных не совсем соответствует распределению тестовых данных.
Можно предположить, что минимумы
на тестовых данных будет немного отличаться от минимумов исходной функции
, в частности,
минимумы, скорее всего, будут сдвинуты относительно друг друга.
Но если широкий минимум не боится подобных искажений, то узкий минимум может измениться до неузнаваемости.
Опять же, давайте посмотрим на картинку выше.
Если предположить, что черный график является исходным
, а красный - тестовый, сразу видно, к каким проблемам это может привести.
На практике было замечено, что градиентный спуск с большими пакетами систематически дает несколько лучшие результаты на обучающем наборе, но проигрывает на тестовом наборе.
Это часто объясняется тем, что небольшие партии вносят шум в оценку целевого распределения и не позволяют ему стабилизироваться.
в узком минимуме[21].
Происходит примерно то же, что и на картинке выше: функция постоянно меняется (на этот раз намеренно), а на месте впадин образуются гребни.
Из узких впадин при таком «перемешивании»
выбрасывается, но не из широких.
Также авторы [21] утверждают, что при обучении с небольшим размером подвыборки
проходит гораздо дальше от точки инициализации, чем в противоположном случае.
Этот показатель описывается термином «исследовательская способность алгоритма градиентного спуска» и также считается благоприятным для достижения хороших результатов.
Теги: #Машинное обучение #машинное обучение #функция потерь #функция потерь #градиентный спуск #градиентный спуск #математика #Машинное обучение
-
10 Шагов К Созданию Отличной Команды
19 Oct, 24 -
Php: Сохранение Объектов В Сеансе
19 Oct, 24 -
[Пятница] Чуи, Нас Обманули
19 Oct, 24


