В этой части я расскажу вам, как я рассчитал вероятности обнаружения агентов в клетках в зависимости от плотности населения пространства.
Д ракоши.
А также как это можно наблюдать Д Ракоши становятся более сознательными жителями своей вселенной.
Кто они Д ракоши заглянуть первая часть .

1. Зачем нам нужны вероятности? 2. Постановка задачи 3. Расчет способов расстановки агентов 4. Моделирование вероятностей методом Монте-Карло 5. Что случилось?
1. Зачем нам нужны вероятности?
Как следить за Д ракоши
Прежде чем мы начнем проводить симуляцию, нам нужно понять, как мы будем «смотреть» на мир.Д ракош? Ведь их будут тысячи, каждый будет заниматься своим делом, куда-то ходить, что-то есть и т. д. Поэтому в самом начале мне пришлось подумать о параметрах, которые бы описывали текущее состояние моделируемой системы и показывали динамику происходящих в ней изменений.
Здесь всего 24 значения, за которыми интересно следить, помимо самого пространства с раздачей агентов и еды.
Среди этих параметров есть вполне очевидные: количество агентов, количество еды в космосе, рождаемость и смертность.
Но подробнее о них речь пойдет в третьей части.
Сейчас я остановлюсь подробнее на специальной группе параметров, которые позволят оценить степень «осведомленности» действий агентов.
Другими словами, отличайте случайное поведение от «сознательного».
Напомню, что агенты могут выполнять шесть разных действий: Проходить , Шаг 1 , Шаг 2 , Есть , Атака , Секс .
Для каждого из них можно посчитать долю агентов, выполняющих его на каждом временном шаге:
,
,
,
,
,
.
Эти шесть параметров позволят вам понять, что они делают. Д ракоши.
Все действия, кроме Проходить может быть успешным или неудачным, в зависимости от текущей ситуации в текущей и соседних ячейках, а также от желания соседа по занятой ячейке.
Для отслеживания успеха используются четыре параметра:
,
,
,
.
Они показывают, какая часть предпринятых действий оказалась успешной.
Более того, оба действия Шаг 1 И Шаг 2 учитываются в одном параметре
.
Индексы осведомленности или зачем нужны вероятности?
На начальном этапе, когда нейронная сеть агентов еще не обучена, действия агентов будут случайными.А по мере эволюционного развития, под влиянием отбора, можно ожидать повышения степени осознанности и, следовательно, увеличения успешности действий.
Но необходимо учитывать, что успех действий зависит и от окружения.
Так что успех действий Шаг 1/2 определяется наличием свободного места в ячейке, которую агент выбрал для перемещения (всего в ячейках имеется два места для агентов).
И это будет зависеть как от правильного выбора агента, так и от количества агентов в космосе.
Текущее количество агентов удобно отслеживать с помощью параметра
– плотность агентов в пространстве, равная отношению количества агентов к числу ячеек в пространстве.
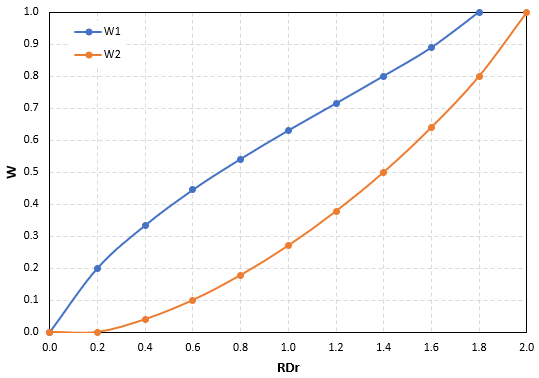
Когда агентов в пространстве мало, плотность близка к нулю и вероятность того, что в выбранной агентом ячейке окажется свободное место, близка к единице.
Поэтому, несмотря на наличие или отсутствие «осведомленности» у агентов при низкой плотности агентов (
) успех действий Шаг 1/2 будет высоким(
).
С увеличением числа агентов вероятность найти свободное место в случайно выбранной ячейке уменьшается вместе с успехом.
, если только выбор ячейки для совершения шага не сделан осознанно.
Когда количество агентов близко к максимальной емкости пространства (
) вероятность найти свободное место станет близкой к нулю (
).
Вы можете ввести параметр для осознанности действий Шаг 1/2 , который мы будем рассчитывать как разницу между текущим успехом
и вероятность найти свободное место в ячейке
:
Здесь
– обозначает вероятность присутствия двух агентов в выбранной ячейке.
Точно так же успех действий Атака И Секс будет зависеть от вероятности (
), что агент найдет другого агента в занимаемой им ячейке.
Осведомленность об атаке можно определить как превышение успеха.
сверхвероятность
:
Но успех
зависит не только от вероятности найти партнера в клетке, но и от вероятности того, что партнер также совершает в данный момент Половое действие.
Но даже если партнер окажется сговорчивым, для успешного полового акта необходимо, чтобы в окружающем пространстве нашлось место для малыша.
Следовательно, вероятность случайного успеха будет произведением вероятностей трех независимых событий:
– в ячейке есть потенциальный партнер,
- партнер также выполняет действие Секс ,
– в ячейке, которую выбрала мать для размещения ребенка, есть свободное место.
Поэтому я предлагаю определить осознанность супружеского поведения следующим образом:
2. Постановка задачи
Для расчета представленных выше индексов осведомленности необходимо научиться рассчитывать две вероятности:И
.
Очевидно, они зависят от плотности агентов в пространстве, а также от равномерности их распределения по пространству.
Но для упрощения расчетов в будущем мы будем предполагать равномерное распределение агентов по пространству.
То есть будем считать, что эти вероятности не зависят от положения агента в пространстве.
Сформулируем задачу следующим образом.
Есть место отДля решения этой проблемы я использовал два подхода.
клетки.В одной ячейке может содержаться не более
агенты.Эти клетки содержат
агенты (
).Необходимо определить вероятность того, что в выбранной ячейке с одним агентом окажется другой агент –
.И вероятность того, что выбранная ячейка будет иметь
агенты –
.
Первый - это расчет вероятности в классическом его понимание как отношение числа различных расположений агентов, благоприятствующих желаемому событию, к общему числу расположений агентов в клетках.
Для расчетов я использовал метод производящих функций.
В второй подход использовал концепцию вероятность частоты .
Расчеты проводились методом Монте-Карло.
Вероятно, существуют и другие способы расчета этих вероятностей, возможно, даже более простые.
Буду признателен за подсказку по этим вопросам.
3. Расчет способов расстановки агентов
Вывод рекуррентной формулы
Предложенный ниже подход к вычислению вероятностей позволяет решить поставленную задачу даже в более общей постановке, когда емкости ячеек различны.
Определим емкости пространственных ячеек в виде последовательности
, Где
– номер ячейки (от
до
).
Для удобства вычислений перенумеруем ячейки так, чтобы ячейка, выбранная для определения вероятностей, имела номер
.
Поставленная задача может быть сведена к подсчету количества способов расположить агентов в ячейках пространства.
Тогда вероятность
– это отношение числа способов расположения агентов, при которых клетка
хотя бы один агент добирается до полного количества способов организовать
агенты по
ячейки пространства.
Для мира Д Ракош емкость всех ячеек равна двум.
Но при расчете
емкость ячейки
принял
, поскольку изначально известно, что в этой ячейке уже есть один агент (см.
определение вероятности
выше).
Вероятность
– это отношение числа способов расположения агентов, при которых клетка
максимальное количество агентов для этой ячейки падает –
, к общему числу способов расположить
агенты по
ячейки пространства.
Обозначим через
количество способов упорядочить
средства для клеток с
на первом.
Также для расчетов нам необходимо знать количество свободных мест в ячейках с
во-первых -
:
Рассмотрим процесс, в котором мы последовательно перебираем все ячейки пространства (начиная с
до
) и на каждом шаге помещаем его в следующую ячейку —
ряд агентов -
пока мы не поставим все на место
неразмещенные агенты или мы не исчерпаем все клетки.
В ячейку
можно разместить из
до
агенты.
Но если агентов осталось меньше, чем максимальная вместимость ячейки, то разместить можно не более
агенты.
Таким образом
.
Количество способов заполнения ячейки агентами представляет собой комбинацию без повторений
К
:
Поместив
агенты на ячейку
, еще будет
агенты для размещения в клетках с
К
.
И каждому
будет соответствовать
способы расстановки остальных агентов.
Работа
– дает нам количество способов размещения
агенты в клетке
И
агенты для остальных клеток.
Суммирование по всем допустимым значениям
, получим необходимое количество способов расстановки:
Чтобы использовать полученную рекуррентную формулу, необходимо задать граничные условия:
- Если
, т.е.у нас не осталось агентов, которых можно поместить в ячейку, то у нас есть только один способ выполнить размещение агентов — никого не помещать в ячейку:
- Для последней ячейки
агентов расставить тоже можно только один - оставить всё
агентов в нем, но только если для них достаточно места:
- Если места для размещения недостаточно
агенты в клетках с
К
, то нет способов заполнить ячейку:
:
Где
– это количество способов расположить агентов, в которых клетка
один или несколько агентов ударили:
Обратите внимание, что здесь мы начинаем суммирование с единицы, поскольку нас интересуют те расположения, при которых ячейка
по крайней мере один агент попадает. Выражения для вероятности
:
Где
– это количество способов расположить агентов, в которых клетка
максимальное количество агентов для этой ячейки падает:
Пример расчета вероятностей для S=5 Рассмотрим пример расчета количества способов расположить агентов в пяти ячейках (
), емкость которого равна двум (
).
Результаты расчета сведены в таблицу: 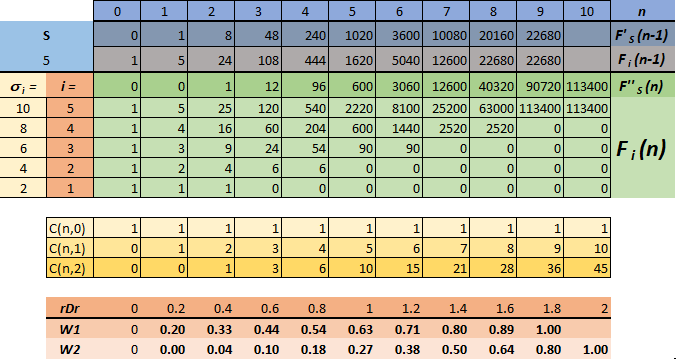
Упрощение и переход к сокращенной форме
Количество мероприятий растет очень быстро и ужеЧисел двойной точности недостаточно.
Даже если вы используете пакеты для символьных вычислений с произвольной точностью (например, Symbolic Math Toolbox и арифметика переменной точности в среде MatLab), проблема переполнения стека рекуррентных вызовов функций с большими размерами пространства остается.
Поэтому полученные выше выражения необходимо преобразовать.
А еще лучше вывести формулу, по которой можно сразу рассчитать
без необходимости читать предыдущие значения.
Первое, что можно сделать, это вынуть из-под знака суммы
.
Но сначала введем обозначения заданное количество аранжировок
агенты по
клетки, которые в
раз меньше:
Маленький алгебраический трюк
Полное количество методов размещения теперь будет таким:
Аналогично для
, и после замены на
мы получаем:
И мы можем сократить выражения для вероятностей факториалом:
Где
После введения новых обозначений необходимо переписать выражения для граничных условий.
Для дальнейших расчетов удобнее представить граничные условия в следующем виде:
-
, в
,
; -
, в
,
; -
, в

-
Вирусы. Вирусы? Вирусы! Часть 1
19 Oct, 24 -
Я Стиль Нестандартно
19 Oct, 24 -
Идеализм В Ит – Помеха Развитию
19 Oct, 24 -
Закругленные Углы Html+Css+Jquery
19 Oct, 24


