Я все еще изучаю базовую математику и механику игры.
Эта статья вторая из серии( Ссылка на первую часть ), продолжает анализировать этапы, пытаться сортировать их по необходимости и изучать различные способы построения маршрутов.
Если проводить аналогии с математикой, то это только основы, арифметика.
Алгебра и высшая математика в духе «взять машины или построить сценуЭ», «Что лучше сейчас построить – сцену или станциюЭ» а "использование одного этапа несколькими маршрутами" пока в стадии планирования, надеюсь руки и мозги до них дойдут.
По умолчанию пост содержит аргументы, актуальные для игры 2-3 игроков (на «двухпутных» участках используется только один путь) Краткая информация о первой части В первой статье с помощью Python и Excel была предпринята попытка понять, какие автомобили выгоднее использовать для построения «серых» участков и как быстро построить тот или иной маршрут.
Из предыдущих разработок будет использоваться только таблица «количество ходов для построения участка длиной N»: 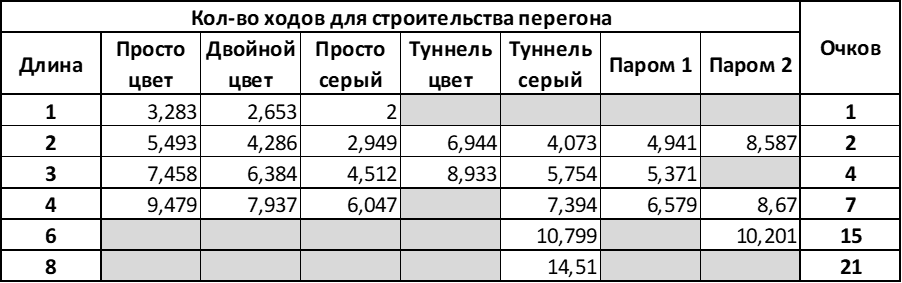
Нахождение наиболее «выгодного» пути
Как показывает игровая практика и комментарии уважаемых участников, кратчайший маршрут между двумя городами не всегда является самым выгодным( если быть совсем честным, почти никогда ).Попробуем найти путь, для которого соотношение «заработанные очки/затраченные ходы» было бы максимальным.
Описание алгоритма поиска пути 1. Для каждой из 46 карт маршрутов производится поиск всех возможных «маршрутов» от начальной точки до пункта назначения.
Для «следов» маршрутов вводим два ограничения: Длина (количество используемых автомобилей) не превышает 45 (максимально возможных автомобилей).
Каждый город можно использовать только один раз (циклы не учитываются).
Все это реализуется с помощью стандартного поиска в глубину.
2. Из всех возможных «путей» выберите тот, для которого соотношение (Очки за пробежки + Очки за маршруты) / (Количество затраченных ходов) самый большой.
Алгоритм оказался довольно медленным; для каждой карты маршрута он перебирал все возможные варианты около полутора минут, съедая при этом 3 гигабайта оперативной памяти.
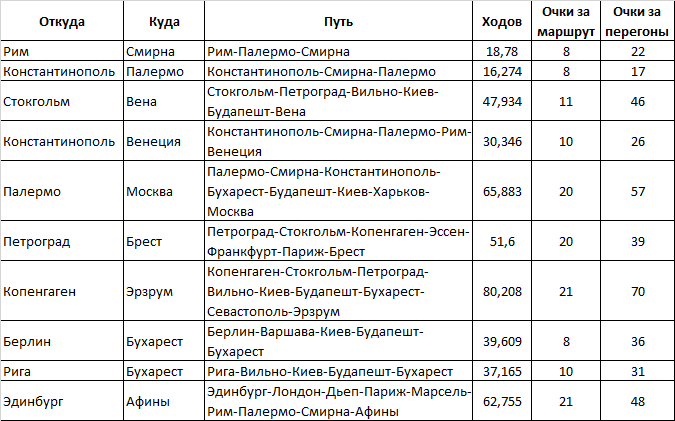
Самые «выгодные» маршруты и маршруты к ним
Результаты выполнения алгоритма иногда давали результаты, которые были совершенно «нелогичны» в глазах человека.
Например, маршрут «Лондон-Берлин» (7 баллов) компьютер предлагает построить так: « Лондон-Дьепп-Париж-Марсель-Рим-Палермо-Смирна-Константинополь-Бухарест-Будапешт-Киев-Варшава-Берлин "(в среднем 101 ход; 81 очко за построенные этапы).
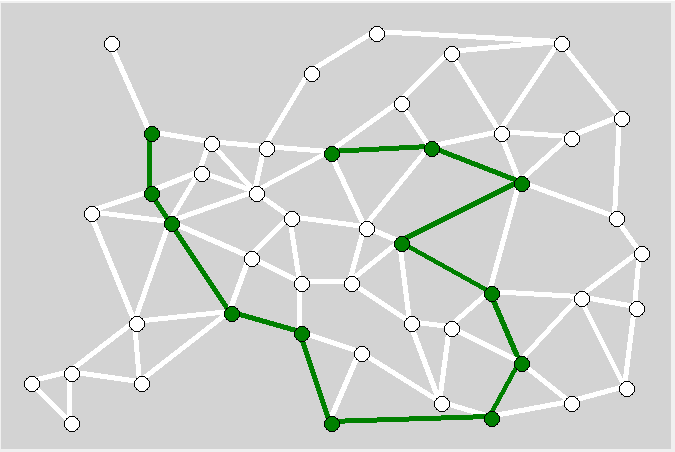
Как говорил мой дедушка-фронтовик: «От Киева через Пензу до Житомира».
После того, как список наиболее «выгодных» маршрутов сформирован, можно переходить к следующим этапам расчетов.
Найдите самые загруженные города
Как и в прошлый раз, для каждого города было рассчитано количество маршрутов, в которых он участвует (как конечная станция и как промежуточная станция).«Затор» рассчитывался как разница между маршрутами из/в город и количеством маршрутов.

Самые загруженные города 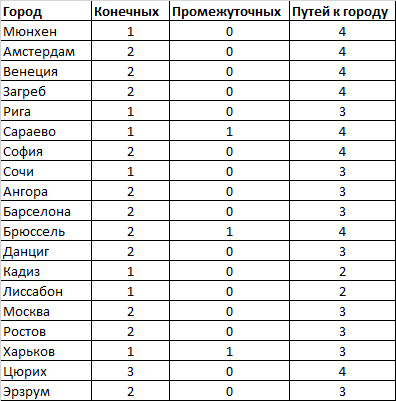
Самые «свободные» города
При расчете загруженности городов учитывалось только количество подъездов к городу; количество треков в этапе (один или два) игнорировалось.
Соответственно, цифры более или менее актуальны для игры вдвоём или втроем.
Ну.
сами по себе таблицы не несут никакой полезной информации, кроме того, что помогут выбрать, с какого города начать строительство, при прочих равных условиях.
Гораздо важнее информация об этапах.
Самые загруженные этапы
Как и в прошлый раз, были проанализированы наиболее «выгодные маршруты», рассчитано использование этапов в них независимо от направления движения (то есть движения типа «Лондон-Динбург» и «Динбург-Лондон» рассматриваются как движения по одному и на одной стадии).
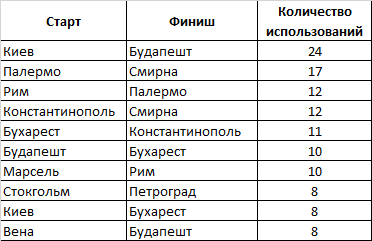
Самые загруженные сцены, их нужно занять в первую очередь 
Этапы, которые не использовались для прокладки маршрутов
В комментариях к предыдущему посту ппрогер И g000phy писал, что для победы в игре необходимо использовать перегоны длиной 8 и 6 вагонов.
Как и ожидалось, в верхней части самой «загруженной» таблицы оказались 6-вагонные участки Киев-Будапешт и Палермо-Смирна, а также подъездные пути к ним.
Неожиданно Стокгольм-Петроград оказался в самом низу рейтинга Топ-10. Видимо, сказывается его удаленность от основных маршрутов и большое количество машин, которые придется потратить на строительство.
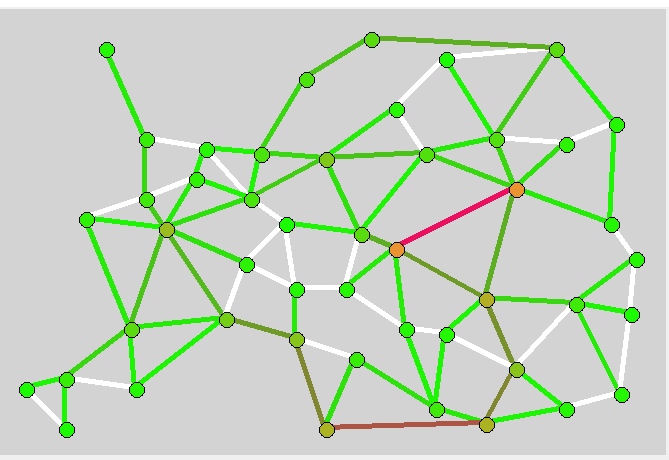
Тепловая карта.
Чем дальше от зеленого, тем более перегружен этот участок/город. Неиспользуемые пути отмечены белым цветом.
Вызовы с наивысшим приоритетом
В комментариях к предыдущему посту дурак написал о ключевых этапах, выход из строя которых приведет к повышенному расходу машин и трасс (яркий пример - этап Харьков-Ростов для восточного сегмента).В процессе поиска этих этапов хотелось бы попросить совета у уважаемого сообщества.
Алгоритм поиска я вижу следующий: Количество ходов, необходимое для построения каждого маршрута, суммируется (получается определенный норматив).
Каждый этап исключается из матрицы путей один за другим.
Опять же подсчитывается сумма ходов, затраченных на каждый маршрут. «Важность» каждого этапа рассчитывается как разница ходов, затраченных на удаленном этапе и стандартном.
В настоящее время для каждого маршрута доступны два варианта «маршрута»: Проложить маршрут из точки А в точку Б за наименьшее количество ходов.
.
Алгоритм описан в предыдущей статье, результат расчета важности приведен ниже: 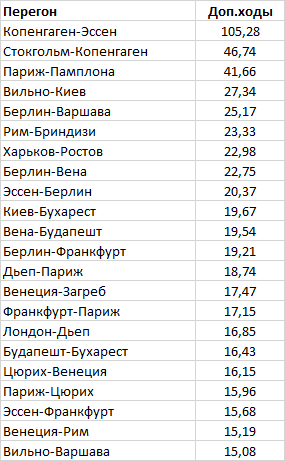
В список не входит «Динбург-Лондон» (если один игрок построит на этом участке вагоны, второй построит станцию или останется с незавершенным маршрутом).
Важность этапов Копенгаген-Эссен, Стокгольм-Копенгаген и Харьков-Ростов также очевидна, но остальной список вызывает сомнения.
Маршрут из точки А в точку Б с наибольшим соотношением «количество полученных очков/количество потраченных ходов» .
В данном случае критические этапы не рассматривались по двум причинам.
Во-первых, это долго (90 перегонов * 46 маршрутов * 1,5 минуты на расчет).
Во-вторых, проложенные «маршруты» маршрутов дают такие «круги», что по большей части их вряд ли можно будет использовать в реальной игре.
Собственно, поиск «ключевых» участков зависит от набора первичных данных (списка логически построенных маршрутов).
Этих «логически построенных маршрутов» под рукой нет, и нет идей, как их найти.
Буду признателен за ваши мысли и предложения.
Продолжение следует (станция, самый длинный путь) следует. Теги: #Игры и игровые приставки #Логические игры #билет на аттракцион #математика в играх #Мир хобби

-
Глобальный Саммит Creative Commons 2011 Г.
19 Oct, 24 -
Миллион С Нуля За 2 Года
19 Oct, 24


