Часто при работе с нейронными сетями мы сталкиваемся с задачей построения линейных решающих функций (ЛДФ) для разделения классов, содержащих наши изображения.
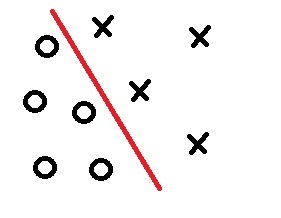
Рис.
1. 2D-случай Одним из методов решения нашей проблемы является алгоритм наименьшей среднеквадратической ошибки (LSEM).
Этот алгоритм интересен не только тем, что он помогает построить нужные нам ФП, но и тем, что в случае возникновения ситуации, когда классы линейно неразделимы, мы можем построить ФП, в котором ошибка ошибочной классификации стремится к минимуму.

Рисунок 2. Линейно неразделимые классы
Ниже приведем исходные данные: 
— обозначение класса (i — номер класса) 
— обучающая выборка 
— метки (номер класса, к которому принадлежит изображение 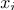
) 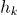
— скорость обучения (произвольное значение)
Этой информации нам более чем достаточно для построения LRF.
Перейдем непосредственно к самому алгоритму.
Алгоритм
1 шаг
а) перевести
в систему

, Где

равно

, в конце которого есть класс изображения Например: Пусть образ будет дан

.
Затем 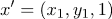
, Если 
с 1 класса 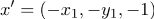
, Если 
со 2-го класса
б) построить матрицу 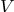
размерность Nx3, состоящая из наших векторов 
в) здание 
г) мы считаем 
Где 
произвольный вектор (по умолчанию — единица измерения)
г) 
(номер итерации)
Шаг 2
Проверка условия остановки: Если
затем «СТОП» в противном случае перейдите к шагу 3
Шаг 3
А)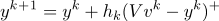
(где + — функция Хевисайда) Например (функция Хевисайда):

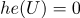
(Если

)

(Если

или

) После вычислений меняем номер итерации:

б) перейти к шагу 2
Пример работы алгоритма NSKO

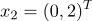
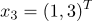
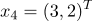

принадлежат к 1-му классу
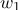

относятся ко 2 классу

А)

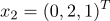
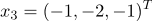

б)
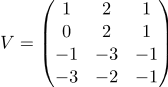
В)

Г)


г)

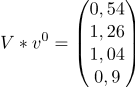
, поскольку все элементы
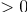

"ОСТАНАВЛИВАТЬСЯ" Мы завершили работу над алгоритмом и теперь можем рассчитать наш LRF.

Спасибо парпалак для онлайн-редактора.
Спасибо за внимание.
Теги: #НСКО #линейные решающие функции #Хо-Кашьяп #Алгоритмы

-
Rails 4. Гибкая Веб-Разработка
19 Oct, 24 -
Micro-Sim: Черт Не Так Страшен
19 Oct, 24 -
Китай За Ющенко! (Пасхалка Из Гугла)
19 Oct, 24 -
Что Модно Пинговать В Этом Сезоне?
19 Oct, 24 -
Mysqlgame
19 Oct, 24 -
Брюс Шнайер Об Алгоритмах Подбора Паролей
19 Oct, 24


