Перевод поста Джона МакЛуна " 10 советов по написанию быстрого математического кода ".
Выражаю огромную благодарность Кириллу Гузенко.
КириллГузенко за помощь с переводом.
В сообщении Джона МакЛуна рассказывается об распространенных методах ускорения кода, написанного на языке Wolfram Language. Тем, кого интересует этот вопрос, рекомендуем посмотреть видеоролик «Оптимизация кода в Wolfram Mathematica», из которого вы подробно и со множеством интересных примеров узнаете о приемах оптимизации кода, рассмотренных как в статье (но подробнее деталь) и другие.
Когда люди говорят мне это Математика недостаточно быстро, я обычно прошу посмотреть код и часто обнаруживаю, что проблема не в производительности Математика , но в его не оптимальном использовании.
Я хотел бы поделиться списком вещей, на которые я обращаю внимание в первую очередь, пытаясь оптимизировать код в Математика .
1. Используйте числа с плавающей запятой и приступайте к ним как можно раньше.
Самая распространенная ошибка, которую я вижу при работе с медленным кодом, — это установка слишком высокой точности для задачи.
Да, неуместное использование точной символьной арифметики — наиболее распространенный случай.
В большинстве компьютерных программных систем нет такого понятия, как точная арифметика — для них 1/3 равна 0,33333333333333. Эта разница может иметь большое значение, когда вы имеете дело со сложными и нестабильными задачами, но для большинства задач подходят числа с плавающей запятой, и, что немаловажно, их вычисления выполняются намного быстрее.
В Математика Любое число с точкой и длиной менее 16 цифр автоматически обрабатывается с машинной точностью, поэтому всегда следует использовать десятичную точку, если в конкретной задаче скорость важнее точности (например, ввод трети как 1./3).
.
Вот простой пример, когда работа с числами с плавающей запятой происходит почти в 50,6 раз быстрее, чем работа с точными числами, которые только потом преобразуются в числа с плавающей запятой.
И в этом случае получается тот же результат. ![]()
![]()
![]()
![]()
То же самое можно сказать и о символьных вычислениях.
Если символическая форма ответа для вас не важна и стабильность не играет особой роли в данной задаче, то постарайтесь как можно скорее перейти на форму с плавающей запятой.
Например, символическое решение этого полиномиального уравнения перед подстановкой значений: Математика строит пятистраничное промежуточное символическое решение.
![]()
![]()
Но если сначала выполнить замену, то Решать будут использовать значительно более быстрые численные методы.
![]()
![]()
При работе со списками данных следует последовательно использовать действительные числа.
Всего одно точное значение в наборе данных превратит его в более гибкую, но менее эффективную форму.
![]()
![]()
![]()
![]()
2. Используйте Скомпилировать .
Функция Скомпилировать принимает код Математика и позволяет заранее указать типы (действительные, комплексные и т. д.) и структуры (значение, список, матрица и т. д.) входных аргументов.
Это лишает язык некоторой гибкости.
Математика , но освобождает вас от необходимости беспокоиться о том: «Что мне делать, если аргумент имеет символическую формуЭ» и другие подобные вещи.
Математика может оптимизировать программу и создать байт-код для запуска ее на своей виртуальной машине (возможна также компиляция на C — см.
ниже).
Не все можно скомпилировать, и очень простой код может не принести никакой пользы, но сложный и низкоуровневый вычислительный код может обеспечить действительно большое ускорение.
Вот пример: ![]()
![]()
![]()
![]()
Применение Скомпилировать вместо Функция обеспечивает ускорение более чем в 80 раз.
![]()
![]()
![]()
Но мы можем пойти дальше, сообщив Скомпилировать о возможности распараллеливания этого кода, получения еще лучших результатов.

![]()
![]()
На своей двухъядерной машине я получил результаты в 150 раз быстрее, чем в исходном случае; Прирост скорости будет еще заметнее при увеличении количества ядер.
Однако помните, что многие функции в Математика , такой как Стол , Сюжет , NИнтегрировать а некоторые другие автоматически компилируют свои аргументы, поэтому вы не увидите никаких улучшений при использовании Скомпилировать для вашего кода.
2.5. и используйте Скомпилировать для генерации кода C.
Кроме того, если ваш код компилируется, вы также можете использовать опцию Цель Компиляции -> "С" для генерации кода C, который автоматически вызовет компилятор C для компиляции его в DLL и отправит ссылку на него в Математика .У нас есть дополнительные накладные расходы на компиляцию, но DLL исполняется непосредственно в процессоре, а не в виртуальной машине.
Математика , поэтому результаты могут быть еще быстрее (в нашем случае в 450 раз быстрее исходного кода).

![]()
![]()
3. Используйте встроенные функции.
Математика содержит множество функций.
За один присест может выучить больше, чем среднестатистический человек (последняя версия Mathematica 10.2 уже содержит более 5000 функций).
Поэтому неудивительно, что я часто вижу код, в котором кто-то реализует некоторые операции, не зная, какие именно.
Математика уже знает, как их реализовать.
И это не просто пустая трата времени на изобретение велосипеда; наши ребята приложили немало усилий, чтобы создать и максимально эффективно реализовать лучшие алгоритмы для различных типов входных данных, чтобы встроенные функции работали очень быстро.
Если вы нашли что-то похожее, но не совсем то же самое, следует проверить параметры и необязательные аргументы — они часто обобщают функции и охватывают множество специализированных и более отдаленных приложений.
Вот пример.
Если у меня есть список из миллиона матриц 2x2, который я хочу превратить в список из миллиона одномерных списков из 4 элементов, то теоретически самым простым способом было бы использовать карта за функцию Сгладить , примененный к списку.
![]()
![]()
![]()
Но Сгладить знает, как решить эту проблему сам, если указать, что уровни 2 и 3 структуры данных должны быть объединены, а уровень 1 не должен затрагиваться.
Указывать такие реквизиты может быть несколько неудобно, но использовать только одну Сгладить , наш код будет выполняться в 4 раза быстрее, чем если бы мы заново изобрели возможности, встроенные в функцию.
![]()
![]()
Поэтому не забудьте просмотреть справку, прежде чем внедрять какие-либо функции.
4. Используйте Вольфрам Верстак.
Математика прощает некоторые виды ошибок в коде, и все будет работать гладко, если вы вдруг забыли инициализировать переменную в нужный момент, и вам не нужно беспокоиться о рекурсии или неожиданных типах данных.
И это здорово, когда вам просто нужно быстро получить ответ. Однако такой глючный код не позволит получить оптимальное решение.
Верстак помогает несколькими способами.
Во-первых, это позволяет лучше отлаживать и организовывать большие проекты, а когда все понятно и организовано, писать хороший код гораздо проще.
Но ключевой особенностью в этом контексте является профилировщик, который позволяет увидеть, какие строки кода используются в определенные моменты времени, сколько раз они вызывались.
Рассмотрим в качестве примера похожий, жутко неоптимальный (с вычислительной точки зрения) способ получения чисел Фибоначчи .
Если вы не задумывались о последствиях двойной рекурсии, вы, вероятно, будете немного удивлены тем, что на оценку уйдет 22 секунды.
выдумка[35] (примерно столько же времени встроенной функции потребуется для расчета всех 208 987 639 цифр Фибоначчи[1000000000] [см.
пункт 3]).
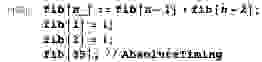
![]()
Запуск кода в Profiler выявляет причину.
Основное правило вызывается 9 227 464 раза, а значение фибо[1] запросили 18 454 929 раз.
Увидеть код таким, какой он есть на самом деле, может стать настоящим откровением.
5. Запомните значения, которые вам понадобятся позже.
Это хороший совет для программирования на любом языке.
Вот как это можно реализовать в Математика : ![]()
Он сохраняет результат вызова ж для любого аргумента, поэтому, если функция вызывается для уже вызванного аргумента, то Математика нет необходимости рассчитывать его еще раз.
Здесь мы отказываемся от памяти, получая взамен скорость, и, конечно, если количество возможных аргументов функции огромно, а вероятность повторного вызова функции с тем же аргументом очень мала, то этого делать не стоит. Но если набор возможных аргументов невелик, то это действительно может помочь.
Этот код сохраняет программу, которую я использовал для иллюстрации совета 3. Вам нужно заменить первое правило следующим: ![]()
И код начинает работать несравнимо быстро, и вычислять выдумка [35] Главное правило следует вызывать только 33 раза.
Запоминание предыдущих результатов предотвращает необходимость многократного рекурсивного спуска к фибо[1] .
6. Распараллельте свой код.
Растет количество операций в Математика автоматически распараллеливаются в локальные ядра (особенно задачи линейной алгебры, обработки изображений, статистики) и, как мы уже видели, могут быть реализованы через Скомпилировать .Но для других операций, которые вы хотите распараллелить на удаленном оборудовании, вы можете использовать встроенные конструкции распараллеливания.
Для этого существует набор инструментов, но в случае принципиально монопоточных задач использование только Параллельная таблица , Параллельная карта И Параллельная попытка может увеличить время вычислений.
Каждая из функций автоматически решает задачи коммуникации, управления и сбора результатов.
При отправке задачи и получении результата есть некоторые дополнительные затраты, то есть выигрывая время в одном, мы теряем время в другом.
Математика поставляется с определенным максимальным количеством доступных вычислительных ядер (в зависимости от лицензии), и вы можете масштабировать их.
сетка Математика , если у вас есть доступ к дополнительным ядрам.
В этом примере Параллельная таблица дает мне двойную производительность, поскольку он работает на моей двухъядерной машине.
Больше процессоров даст больший выигрыш.
![]()
![]()
![]()
![]()
Все, что он может сделать Математика , можно распараллелить.
Например, вы можете отправлять наборы параллельных задач на удаленные устройства, каждая из которых компилируется и выполняется на языке C или на графическом процессоре.
6.5. Рассмотрите возможность использования CUDALink И ОпенКЛЛинк.
С помощью графического процессора некоторые задачи можно решать гораздо быстрее параллельно.
Если ваша проблема не требует функций, уже оптимизированных для CUDA, вам придется немного поработать, но инструменты CUDALink И OpenCLLink автоматизировать для вас большое количество рутинных задач.
7. Используйте Сеять И пожинать накапливать большие объемы данных (но не Добавить в ).
Благодаря гибкости структур данных в Математика, Добавить в не могу знать, что вы будете добавлять номер, потому что с таким же успехом вы можете легко добавить документ, звук или изображение.
Как результат Добавить в необходимо создать новую копию всех данных, реструктурированную для размещения прикрепленной информации.
По мере накопления данных работа будет замедляться (и проектирование данные = Добавить [данные, значение] эквивалент Добавить в ).
Вместо этого используйте Сеять И пожинать .
Сеять передает значения, которые вы хотите собрать, и пожинать собирает их и в конце создает объект данных.
Следующие примеры эквивалентны: ![]()
![]()
![]()
![]()
8. Используйте Блокировать И С вместо Модуль .
Блокировать (локализация значения переменной), С (замена переменных во фрагменте кода на их конкретные значения с последующей оценкой всего кода) и Модуль (локализация имен переменных) — это предельные конструкции, имеющие несколько иные свойства.
По моему опыту, Блокировать И Модуль взаимозаменяемы как минимум в 95% случаев, с которыми я сталкиваюсь, но Блокировать обычно работает быстрее, а в некоторых случаях С (на самом деле Блокировать с переменными, доступными только для чтения) еще быстрее.
![]()
![]()
![]()
![]()
9. Не переусердствуйте с шаблонами.
Шаблонные выражения великолепны.
Многие проблемы можно легко решить с их помощью.
Однако шаблоны не всегда работают быстро, особенно такие нечеткие, как ПустойNullSequence (обычно пишется как «___»), который может долго и упорно искать закономерности в данных, которых там явно не может быть.
Если важна скорость выполнения, используйте четкие модели или вообще избегайте шаблонов.
В качестве примера приведу элегантный способ реализации пузырьковая сортировка в одну строку кода через шаблоны: ![]()
![]()
В теории это красиво, но слишком медленно по сравнению с процедурным подходом, который я изучил, когда впервые начал программировать: 
![]()
Конечно, в этом случае вам следует использовать встроенную функцию Сортировать (см.
совет 3), который работает быстрее всего.
![]()
![]()
10. Используйте разные подходы.
Одна из самых сильных сторон Математика - умение решать проблемы разными способами.
Это позволяет вам писать код так, как вы думаете, а не переосмысливать проблему в соответствии со стилем языка программирования.
Однако концептуальная простота не всегда означает вычислительную эффективность.
Иногда идея, которую легко понять, требует больше работы, чем необходимо.
Но другой момент заключается в том, что благодаря разного рода специальным оптимизациям и умным алгоритмам, которые автоматически применяются в Математика, Часто становится трудно предугадать, какой путь выбрать.
Например, вот два способа вычисления факториала, но второй более чем в 10 раз быстрее.
![]()
![]()
![]()
![]()
Почему? Вы можете догадаться, что Делать медленнее через циклы или все эти назначения Набор К температура потребуется время, или что-то еще не так с первой реализацией, но настоящая причина, вероятно, в порядке
Теги: #язык wolfram #Wolfram Mathematica #ускорение кода #компиляция #распараллеливание #cuda #opencl #программирование #Алгоритмы #Функциональное программирование
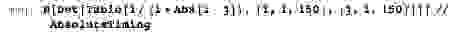
-
Основы Статистики: Просто О Сложных Формулах
19 Oct, 24


