Все мы со школы знаем, что такое системы счисления (СС).
Но не все задумываются о том, насколько дорого стоит CC. Те.
какой набор цифр нам нужен для представления числа в этом СС.
Когда у нас есть ограниченный набор уникальных элементов (цветных камешков разного размера), с помощью которых мы можем представить число, какое максимальное число мы можем представить, используя эти элементы? (все красные камешки – ноль, зеленые – один, синие – два и т. д., маленькие – ноль, средние – первые, большие – вторые и т. д.).
Где та черта, у которой основание СС играет большую роль, чем разрядность числа? Возьмем для примера n - количество элементов, равное 60. Разделив элементы на 2 группы (двоичная система счисления) получим 30 цифр.
30 единиц - это максимум 30-битное число с основанием 2. Если прибавить к нему 1, то получится единица с 30 нулями, т.е.
2 в 30-й, так как каждый ноль - это степень двойки, а цифры начинаются с 0. , и не забудем вычесть тот, который мы добавили.
Для других СС аналогично
, где y — максимальное число, x — основание степени.
Точки строительства:
.
.
График функции: 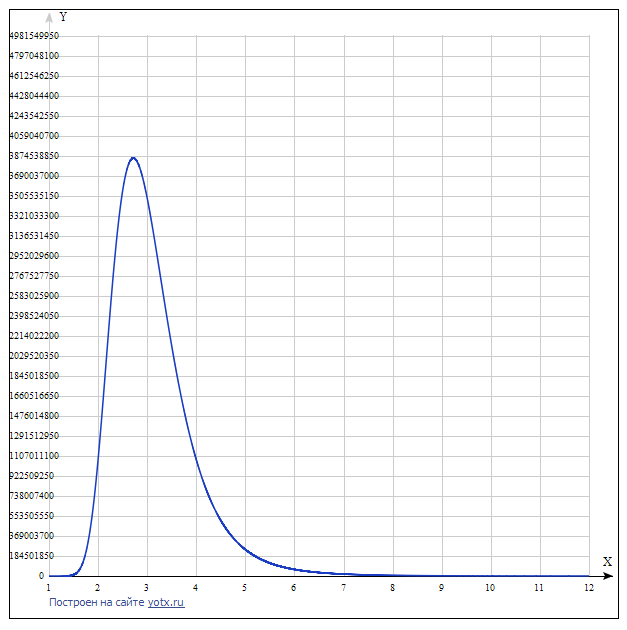
На графике видно, что по мере увеличения базы СС, начиная с трёх, увеличивается её стоимость и функция имеет верхний экстремум.
Приведя его к общему виду, можно получить
, а максимум функции
достигнуто в
.
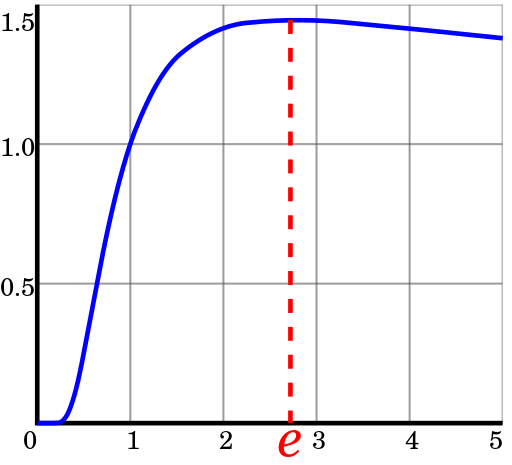
График функции
Те.
Самая экономичная СС — это система, максимально приближенная к
или 3.
P.S.: Кроме того, СС с основанием 3 нечетное, а значит нет проблемы округления (0,5 уменьшить до 0 или 1), а если цифры писать симметрично (-1,0,1 вместо 0,1,2) тогда появляется простота представлений отрицательных чисел (10-1 это 8, -101 это -8, где минус не знак, а часть числа, которую можно заменить на Z), но это совсем другая арифметика)))
Теги: #математика #системы счисления #занимательная математика #число Эйлера
-
Не Поддавайтесь На Провокации!
19 Oct, 24


