А что, если мы возьмем замечательную математику (а именно линейные уравнения) и нашу не менее замечательную JavaScript , а затем положить одно поверх другого? Учитывая ограничения и специфику среды JS, простая математическая задача может превратиться в очень интересную задачу, полную подводных камней в среде JS. На прошлой конференции СвятойJS 19 в Москве одно такое линейное уравнение (помимо других задач от компании СЭМраш ) вызвало немало шума.

И да, это снова раздел Развлекательного JavaScript: прошу всех неравнодушных к коту.
Предыдущие задачи Снежный день Запутывание скобок Самый короткий мемомайзер Конечно, все описанное ниже – это всего лишь несерьезная попытка симбиоза двух замечательных вещей с целью развлечения – к этому не следует относиться серьезно.
И этого материала не было бы, если бы не живой интерес участников конференции, за что им отдельное спасибо!
Формулировка
1. Найдите все целочисленные решения уравнения:2. Найдите все целые решения уравнения:9 +~ x >> 6 / 3 = -x / 3
9 +~ x >> 6 / 3 = -x / 3 | 0
Второе уравнение отличается от первого лишь дополнительной операцией в правой части.
Математическое приближение
Давайте посмотрим на первое уравнение.
И сначала давайте посмотрим на приоритеты используемых операций, согласно таблице : (9 +(~ x)) >> (6 / 3) = -x / 3
Берем поразрядное отрицание Икс , затем складываем с 9. Результат сложения побитно сдвигается вправо на количество бит, равное результату деления 6 на 3.
Очевидно, проблема заключается в использовании побитовых операций над искомыми.
Икс .
Но чтобы найти какой-то условный корень для дальнейших рассуждений, стоит попытаться привести уравнение к приближенному математическому аналогу.
Побитовые операции операнды работают как 32-битные целые числа со знаком.
Побитовое НЕ можно заменить на целое число отрицание приращения: (9 -(x + 1)) >> (6 / 3) = -x / 3
(8 - x) >> 2 = -x / 3
Побитовый сдвиг вправо (с сохранением знака) можно заменить на целое число деление на два в степени, равной операнду справа: (8 - x) / 2^2 = -x / 3
(8 - x) / 4 = -x / 3
Конечно, эти замены весьма условны, и об этом мы поговорим позже.
И вот мы имеем обыкновенное линейное уравнение, единственный корень которого равен -24. Подставим значение в левую и правую часть исходного уравнения: 9 +~ (-24) >> 6 / 3; // = 8
-(-24) / 3; // = 8
Обе части равны, а значит все не так безнадежно и -24 действительно решение.
Перебор для ленивых
Если мы нарисуем графики функций f1(x) = (8 -x)/4 И f2(x) = -x/3 , то мы, конечно, найдём единственную точку пересечения двух прямых в х = -24 .
Но мы сделали в левом выражении пару неравных подстановок с поразрядными операциями, так что в реальности график функции ф1 будет немного отличаться.
Для любого Икс значение функции будет целым числом, отличным от значения на непрерывной линии ф1 с возможным сдвигом в диапазоне от -1 до 1. Это означает, что мы можем ограничить область поиска решений слева и справа от -24, где значения функции ф1 И f2 начинают отличаться более чем на единицу.
Чтобы найти границы области поиска, можно 1) решить неравенство с модулем или 2) внимательно рассмотреть графики функций.
Мы найдем это Икс Стоит посмотреть в интервале [-36, -12]: | (8 - x) / 4 + x / 3 | <= 1

Чтобы перечислить полные решения в некотором замкнутом диапазоне [просить, закончить] давайте напишем функцию найтиx : const findx = (f, beg, end) =>
[.
Array(end - beg + 1)].
map((_, i) => i + beg).
filter(f);
Функция возвращает массив целых чисел, для которых значение переданной функции ж сводится к истинный .
Чтобы найти решения, мы представляем уравнение в виде js-функции, используя оператор равенства: let eq1 = x => 9 +~ x >> 6 / 3 == -x / 3;
findx(eq1, -36, -12); // [-24, -21, -18, -15]
Таким образом, Икс = [-24, -21, -18, -15] — искомые решения первого уравнения.
Графическое решение
Перебор конечно удался, но давайте все же посмотрим на график функции ф1 до конца и решить уравнение графически.Более того, решение не требует знания консоли браузера.
Побитовый оператор НЕ просто отбрасывает дробную часть, поэтому результат -(х+1) будет округлено в меньшую сторону.
Оператор битового сдвига немного сложнее.
Мы заменили его целочисленным делением, но в зависимости от знака делимого числа эта операция округляет результат либо в меньшую, либо в большую сторону: 10 >> 2; // = 2
-10 >> 2; // = -3
Однако мы знаем, что то, что мы ищем Икс находится в диапазоне [-36, -12].
Соответственно, левый операнд битового сдвига ( 8-х ) - в диапазоне [20, 44], т. е.
всегда положительно.
Что, в свою очередь, означает целочисленное деление с округлением в меньшую сторону.
Поняв суть операций, мы сможем нарисовать правильный график функции ф1 :
Найдем четыре точки пересечения функций в одних и тех же координатах.
Икс = [-24, -21, -18, -15].
Второе уравнение
Итак, мы приходим ко второму уравнению: 9 +~ x >> 6 / 3 = -x / 3 | 0
Он отличается от первого добавлением побитового ИЛИ.
Если правый операнд такой операции равен нулю, то результатом будет просто значение левого операнда с отброшенной дробной частью.
Для начала пройдемся по тому же поиску, только определимся с областью поиска.
Поскольку теперь функция f2 имеет сходный характер с ф1 , то для надежности стоит просуммировать возможный сдвиг и ограничить поиск тем местом, где функции отличаются по абсолютной величине более чем на две единицы — это [-48, 0].
let eq2 = x => 9 +~ x >> 6 / 3 == -x / 3 | 0;
findx(eq2, -48, 0); // [-24, -21, -18, -15]
И мы получили одинаковые ответы.
Есть подозрение, что что-то все-таки не так.
Но дело в том, что представляя исходное уравнение такой js-функцией, мы объединили два выражения (левое и правое) через оператор равенства в одно.
А у оператора равенства есть свой приоритет, который выше приоритета побитового ИЛИ.
Функция идентична следующей: x => (9 +~ x >> 6 / 3 == -x / 3) | 0;
В этом случае побитовое ИЛИ не имеет никакого эффекта, поскольку правда | 0 = 1 .
Чтобы этого избежать, необходимо явно указать в теле функции, что мы сравниваем результаты двух подвыражений: let eq2 = x => (9 +~ x >> 6 / 3) == (-x / 3 | 0);
findx(eq2, -48, 0); // [-32, -29, -28, -26, -25, -24, -23, -22, -21, -19, -18, -15]
Количество решений увеличилось.
Теперь посмотрим на графики функций.
По аналогии с ф1 модифицированная функция строится по «лестнице» f2 : 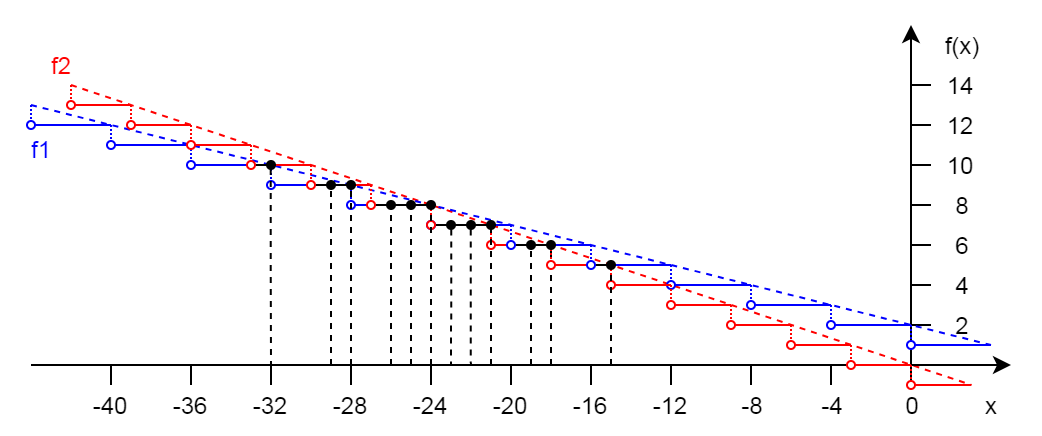
В некоторых местах графики функций перекрывают друг друга, но нас интересуют только точки с целочисленным значением координаты.
Икс : [-32, -29, -28, -26, -25, -24, -23, -22, -21, -19, -18, -15], всего 12 решений.
Пересечения двух «лестниц» с шагами 3 и 4 при желании можно найти алгоритмически.
Дополнительный вопрос
В задаче, предложенной на конференции, был дополнительный вопрос: требовалось найти минимальное решение уравнения 2. Однако не сказано, что это обязательно целое число, поэтому ответ Икс = -32 - оказывается неверным.Невозможно найти решение методом перебора, но его очень легко решить графически.
Это ближайшее значение Икс до -33 справа: 
Кажется, что Икс = -32.(9).
Но это по-прежнему неправда.
Поскольку наша среда — JavaScript, мы ограничены в представлении чисел используемым типом данных.
Тип числа — float64 — числа двойной точности с плавающей запятой (ИИЭР 754).
Запомнить это и дать приблизительную точность оказалось достаточно, чтобы получить плюшевую лису!
Темная сторона побитовых операций
Как упоминалось выше, побитовые операции преобразуют операнды в 32-битные числа, представленные последовательностью 0 и 1 — диапазон [-2147483648, 2147483647].Если число в него не умещается, то старшие биты будут отброшены.
В первом уравнении это не играет никакой роли, так как в правой части нет побитовой операции.
А вот во втором такое преобразование чисел создает интересный эффект.
Например, число -24 будет представлено как: 11111111111111111111111111101000
Отрицательное число получается путем инвертирования (побитового НЕ) битов положительного числа и добавления единицы.
Любое число вне диапазона после завершения преобразования в эту 32-битную последовательность будет идентично в двоичных операциях числу -24. Например, это цифры: 4294967272 | 0; // -24
8589934568 | 0; // -24, prepend '1'
12884901864 | 0; // -24, prepend '10'
17179869160 | 0; // -24, prepend '11'
21474836456 | 0; // -24, prepend '100'
// .
В правой части уравнения перед побитовой операцией делим Икс на 3. Давайте найдём это Икс среди «эквивалентов» есть -24, которое делится на 3. Ближайшее такое число — 12884901864. Подставим его в уравнение: 9 +~ 12884901864 >> 6 / 3 = -12884901864 / 3 | 0
9 +~ 12884901864 >> 2 = -4294967288 | 0
9 + 23 >> 2 = 8
8 = 8
Результат деления на 3 (-4294967288) не умещается в отведенные 32 бита; при инвертировании битов знак со временем теряется и остается только 8: 00000000000000000000000000001000
Дополнительно вы можете проверить корректность результата, вызвав функцию уравнение 2 : eq2(12884901864); // true
Если вдуматься, то рядом с этим корнем можно найти проекции остальных 11 целочисленных решений.
Таким образом, появляется огромное количество новых решений, и рассматривается только ближайший положительный эквивалент -24. Однако все это уже не так интересно, как основная задача, и при анализе решений участников столь редкие ответы оценивались отдельно.
Чтобы избежать путаницы, в условие задачи можно добавить ограничение на требуемые целые числа как знаковые 32-битные.
Или вам не обязательно! Затем, чтобы найти самый маленький корень, следует обратить внимание на окружение Номер.
MAX_SAFE_INTEGER со знаком минус, так как это целое число и float64 с предельной точностью.
Ну, тогда самостоятельно.
Заключение
По итогам конференции большинство участников решили проблему методом перебора, при этом дальность поиска была совершенно разной по разным причинам.Но, как мы видели, этого достаточно для работы с ~50 целыми числами.
Многие попали в ловушку с операционными приоритетами.
Кто-то решил еще и графически, что меня порадовало.
Единицы удивили, выйдя за рамки 32 цифр.
Для продвижения дальше по задачам можно было также использовать грубую силу.
Но чтобы получить дополнительный приз, все равно необходимо было провести некоторый математический анализ.
Очень надеюсь, что идея такой нетипичной задачи, как развлечение для формата конференции, вам понравилась.
За последний год у меня накопилось несколько таких «занимательных» задач на JavaScript. Я решил собрать их все в одном месте.
Пройдите по ссылке, если не боитесь: Неожиданный вызов JavaScript .
Задания Выглядеть комплексно И Сломанная труба , которые также были предложены на конференции, уже размещены.
Да, таких коллекций много, но эта моя! Еще раз спасибо всем.
Теги: #математика #JavaScript #Ненормальное программирование #holyjs #holyjs #challenge

-
Что Такое Blogger.com?
19 Oct, 24 -
Начинаем Вести Видеоблог
19 Oct, 24 -
Удобный Для Пальцев Интерфейс
19 Oct, 24 -
Древовидные Объекты В Джанге
19 Oct, 24


