Полтора года назад я опубликовал статью «Математика на пальцах: методы наименьших квадратов» , который получил весьма достойный отклик, в том числе и то, что я предложил нарисовать сову.
Ну, раз это сова, значит, надо еще раз объяснить.
Ровно через неделю я начну читать несколько лекций студентам-геологам на эту тему; Пользуюсь случаем, чтобы представить здесь (адаптированные) основные тезисы в виде проекта.
Моя главная цель – не дать готовый рецепт из книги о вкусной и здоровой пище, а рассказать, почему так и что еще есть в соответствующем разделе, ведь связи между разными разделами математики наиболее интересны! Сейчас я разобью текст следующим образом:
- Ликбез по теории вероятностей (вступительная статья, по желанию)
- Введение в системы линейных уравнений
- Методы конечных элементов
- Минимизация квадратичных форм и примеры задач наименьших квадратов
- От наименьших квадратов к нейронным сетям
Этот текст предназначен для третьего курса нашего геологического факультета, а это значит (с точки зрения задействованной аппаратуры!), что заинтересованный старшеклассник при соответствующем усердии должен быть в состоянии его понять.
Насколько действительна эта теория или вы верите в теорию эволюции? Однажды меня спросили, верю ли я в теорию эволюции.
Сделайте паузу прямо сейчас, подумайте, как вы на него ответите.

Лично я опешил и ответил, что нахожу это правдоподобным и что вопрос о вере здесь вообще не возникает. Научная теория имеет мало общего с верой.
Короче говоря, теория лишь строит модель окружающего нас мира; нет необходимости в это верить.
Более того, Критерий Поппера требует, чтобы научная теория была фальсифицируемой.
А здравая теория должна, прежде всего, обладать предсказательной силой.
Например, если вы генетически модифицируете сельскохозяйственные культуры, чтобы они сами производили пестициды, вполне логично, что появятся насекомые, устойчивые к пестицидам.
Однако гораздо менее очевидно, что этот процесс можно замедлить, выращивая традиционные растения рядом с генетически модифицированными.
На основе теории эволюции было проведено соответствующее моделирование.
такой прогноз и он, кажется, подтвержденный .
При чем тут наименьшие квадраты?
Как я упоминал ранее, я буду подходить к методу наименьших квадратов, используя принцип максимального правдоподобия.Проиллюстрируем примером.
Допустим, нас интересуют данные о росте пингвинов, но мы можем измерить лишь некоторых из этих красивых птиц.
Вполне логично ввести в задачу модель распределения роста — чаще всего она нормальная.
Нормальное распределение характеризуется двумя параметрами – средним значением и стандартным отклонением.
Для каждого фиксированного значения параметра мы можем вычислить вероятность того, что будут сгенерированы именно те измерения, которые мы сделали.
Далее, варьируя параметры, найдем те, которые максимизируют вероятность.
Таким образом, чтобы работать с максимальным правдоподобием, нам нужно действовать в терминах теории вероятностей.
Ниже мы определим понятия вероятности и правдоподобия, но сначала хотелось бы остановиться на другом аспекте.
Я на удивление редко вижу, чтобы люди думали о слове «теория» во фразе «теория вероятностей».
Что изучает теоретик?
Ожесточенные споры о происхождении, значении и сфере применимости вероятностных оценок ведутся уже более ста лет. Например, Бруно Де Финетти заявил, что вероятность — это не что иное, как субъективный анализ вероятности того, что что-то произойдет, и что эта вероятность не существует вне разума.Это готовность человека сделать ставку на что-то происходящее.
Это мнение прямо противоположно мнению классика/частые посетители о вероятности конкретного исхода события, при котором предполагается, что одно и то же событие может повторяться много раз, а «вероятность» конкретного исхода связана с частотой возникновения конкретного исхода при повторных испытаниях.
Помимо субъективистов и частотистов, есть еще объективисты, которые утверждают, что вероятности — это реальные аспекты вселенной, а не просто описания степени уверенности наблюдателя.
Как бы то ни было, все три научные школы на практике пользуются одним и тем же аппаратом, основанным на аксиомах Колмогорова.
Приведем косвенный аргумент, с субъективистской точки зрения, в пользу теории вероятностей, построенной на аксиомах Колмогорова.
Сами аксиомы мы представим чуть позже, а сначала предположим, что у нас есть букмекерская контора, принимающая ставки на следующий чемпионат мира.
Пусть у нас есть два события: а = чемпионом станет команда Уругвая, б = чемпионом станет команда Германии.
Букмекерская контора оценивает шансы команды Уругвай на победу в 40%, шансы команды Германии – в 30%.
Очевидно, что Германия и Уругвай не могут победить одновременно, поэтому вероятность a∧b равна нулю.
Ну и при этом букмекерская контора считает, что вероятность того, что выиграет либо Уругвай, либо Германия (а не Аргентина или Австралия), составляет 80%.
Запишем это следующим образом: 
Если букмекерская контора заявляет, что его уровень уверенности в событии А равно 0,4, то есть П(а) = 0,4, то игрок может выбрать, будет ли он делать ставку за или против утверждения.
А суммы ставок, соответствующие степени доверия букмекерской конторы.
Это означает, что игрок может сделать ставку на то, что событие произойдет. А произойдет, поставив четыре рубля против букмекерских шести рублей.
Или игрок может поставить на событие шесть рублей вместо букмекерских четырех рублей.
А не случится.
Если уровень доверия букмекера неточно отражает состояние мира, то можно рассчитывать на то, что он потеряет деньги в долгосрочной перспективе из-за игроков, чьи убеждения более точны.
Более того, в данном конкретном примере у игрока есть стратегия, при которой букмекерская контора Всегда теряет деньги.
Давайте проиллюстрируем это: 
Игрок делает три ставки, и каким бы ни был исход чемпионата, он всегда выигрывает. Обратите внимание, что при расчете суммы выигрыша в принципе не учитывается, являются ли Уругвай или Германия фаворитами чемпионата; Проигрыш букмекера гарантирован! К такой ситуации привело то, что букмекерская контора не руководствовалась основами теории вероятностей, нарушив третью аксиому Колмогорова, приведем все три: 
В текстовом виде они выглядят так:
- 1. Все вероятности находятся в диапазоне от 0 до 1.
- 2. Безоговорочно истинные утверждения имеют вероятность 1, а безусловно ложные утверждения имеют вероятность 0.
- 3. Третья аксиома – аксиома дизъюнкции, ее легко понять интуитивно, заметив, что в тех случаях, когда утверждение а верно, наряду с теми случаями, когда б истинно, безоговорочно охватывает все те случаи, когда утверждение a∨b истинно; но в сумме двух наборов случаев их пересечение происходит дважды, поэтому необходимо вычесть P(a∧b).
Если букмекерская контора руководствуется множественными степенями уверенности, что нарушает аксиомы теории вероятностей, то существует комбинация ставок игрока, гарантирующая проигрыш букмекерской конторы (выигрыш игрока) по каждой ставке.Аксиомы вероятности можно рассматривать как ограничивающие набор вероятностных убеждений, которых может придерживаться некоторый агент. Обратите внимание, что следование букмекерской конторой аксиомам Колмогорова не означает, что он выиграет (оставим в стороне вопросы комиссий), но при их несоблюдении он гарантированно проиграет. Обратите внимание, что в пользу использования вероятностей были выдвинуты и другие аргументы; но именно практичный Успех систем вероятностного рассуждения оказался привлекательным стимулом, заставившим пересмотреть многие взгляды.
Итак, мы слегка приоткрыли завесу того, о чем Почему Теорвер может иметь смысл, но какими именно объектами он манипулирует? Вся теория построена всего на трёх аксиомах; все три выполняют какую-то магическую функцию п .
Более того, глядя на эти аксиомы, это очень напоминает мне функцию площади фигуры.
Давайте попробуем проверить, работает ли площадь для определения вероятности.
Давайте определим слово «событие» как «подмножество единичного квадрата».
Определим слово «вероятность события» как «площадь соответствующего подмножества».
Грубо говоря, у нас есть большая картонная мишень, мы закрываем глаза и стреляем по ней.
Шансы на попадание пули в данный набор прямо пропорциональны площади набора.
Достоверным событием в данном случае является весь квадрат, а заведомо ложным событием, например, любая точка квадрата.
Из нашего определения вероятности следует, что невозможно идеально попасть в точку (наша пуля — материальная точка).
Я очень люблю картинки, рисую их много, и Theorver не исключение! Проиллюстрируем все три аксиомы: 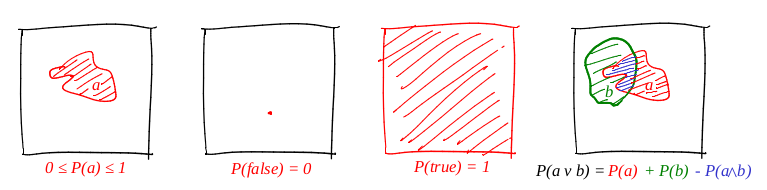
Итак, первая аксиома удовлетворена: площадь неотрицательна и не может превышать единицы.
Достоверное событие — это весь квадрат, а заведомо ложное событие — любой набор нулевой площади.
И это прекрасно работает с дизъюнкцией!
Максимальная вероятность с примерами
Пример первый: подбрасывание монеты
Давайте рассмотрим простейший пример подбрасывания монеты, он же Схема Бернулли .Держал н эксперименты, в каждом из которых может произойти одно из двух событий («успех» или «неудача»), одно с вероятностью п , второй с вероятностью 1-п .
Наша задача – найти вероятность получения именно к успехов в этих н эксперименты.
Эту вероятность нам дает формула Бернулли: 
Возьмем обычную монету( р=0,5 ), подбросьте его десять раз ( п=10 ), и посчитайте, сколько раз выпадет решка: 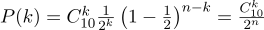
Вот как выглядит график плотности вероятности: 
Таким образом, если мы зафиксировали вероятность наступления «успеха» (0,5), а также зафиксировали количество экспериментов (10), то возможное количество «успехов» может быть любым целым числом от 0 до 10, но эти результаты не являются с равной вероятностью.
Совершенно очевидно, что получить пять «успехов» гораздо более вероятно, чем ни одного.
Например, вероятность выпадения семи орлов составляет примерно 12%.
Теперь посмотрим на ту же проблему с другой стороны.
У нас есть реальная монета, но мы не знаем ее распределения априорной вероятности «успеха»/«неуспеха».
Однако мы можем подбросить его десять раз и посчитать количество «успехов».
Например, у нас получилось семь голов.
Как это поможет нам оценить п ?
Можно попробовать исправить в формуле Бернулли н =10 и к =7, уходя п свободный параметр: 
Тогда формулу Бернулли можно интерпретировать как авторитет оцениваемый параметр (в данном случае п ).
Я даже поменял букву функции, теперь она л (от английского подобия).
То есть правдоподобие — это вероятность генерации наблюдения (7 голов из 10 испытаний) для заданного значения параметра(ов).
Например, вероятность сбалансированной монеты ( п =0,5) при условии, что семь голов из десяти бросков примерно равны 12%.
Вы можете построить график функции л : 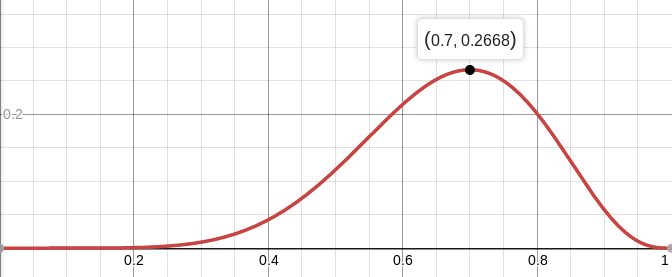
Итак, мы ищем такое значение параметра, которое максимизирует вероятность получения тех наблюдений, которые у нас есть.
В данном конкретном случае у нас есть функция одной переменной, мы ищем ее максимум.
Чтобы было легче искать, буду искать как можно больше л , А журнал L .
Логарифм — строго монотонная функция, поэтому максимизация того и другого — строго одно и то же.
А логарифм делит произведение на сумму, которую дифференцировать гораздо удобнее.
Итак, ищем максимум этой функции: 
Для этого приравняем ее производную нулю: 
Производная log x = 1/x, получаем: 
То есть максимальная вероятность (приблизительно 27%) достигается в точке 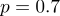
На всякий случай вычислим вторую производную: 
В точке p=0,7 она отрицательна, поэтому эта точка действительно является максимумом функции L. 
А вот как выглядит плотность вероятности для схемы Бернулли с п = 0.7: 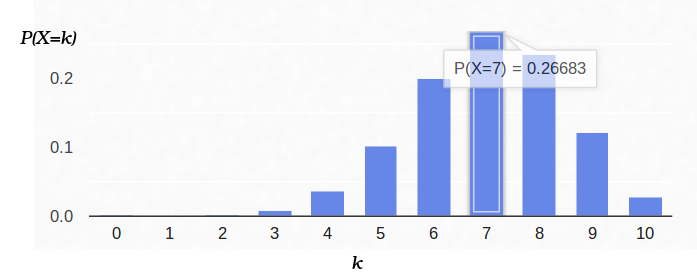
Пример второй: АЦП
Представим, что у нас есть некая постоянная физическая величина, которую мы хотим измерить, будь то длина линейкой или напряжение вольтметром.Любое измерение дает приближение это количество, но не само количество.
Описываемые здесь методы были разработаны Гауссом в конце XVIII века, когда он измерял орбиты небесных тел.
Например, если мы измерим напряжение на аккумуляторе N раз, мы получим N разных измерений.
Какой из них мне следует взять? Все! Итак, пусть у нас есть N значений Uj: 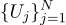
Предположим, что каждое измерение Uj равно идеальному значению плюс гауссов шум, который характеризуется двумя параметрами – положением гауссова колокола и его «шириной».
Вот как выглядит плотность вероятности: 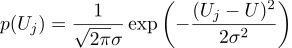
То есть, учитывая N заданных значений Uj, наша задача — найти параметр U, который максимизирует значение правдоподобия.
Вероятность (я сразу беру от нее логарифм) можно записать так: 
Ну а дальше все строго по-прежнему, приравняем нулю частные производные по искомым нами параметрам: 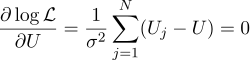
Получаем, что наиболее вероятную оценку неизвестной величины U можно найти как среднее всех измерений: 
Ну а наиболее вероятный сигма-параметр — это обычное стандартное отклонение: 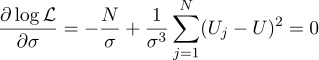

Стоило ли заморачиваться с получением простого среднего значения всех измерений в вашем ответе? На мой взгляд, оно того стоило.
Кстати, усреднение нескольких измерений постоянной величины с целью повышения точности измерений – вполне стандартная практика.
Например, Усреднение АЦП .
Кстати, для этого не требуется гауссов шум; достаточно того, чтобы шум был несмещенным.
Пример третий, и снова одномерный
Продолжая разговор, возьмем тот же пример, но немного усложним его.Мы хотим измерить сопротивление определенного резистора.
Используя лабораторный блок питания, мы можем пропустить через него определенное эталонное количество ампер и измерить необходимое для этого напряжение.
То есть у нас будет N пар чисел (Ij, Uj) в качестве входных данных для нашей оценки сопротивления.
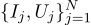
Нарисуем эти точки на графике; Закон Ома говорит нам, что мы ищем наклон синей линии.

Запишем выражение для правдоподобия параметра R: 
И снова приравниваем соответствующую частную производную нулю: 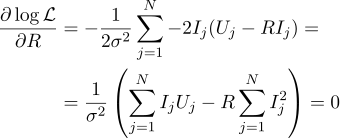
Тогда наиболее правдоподобное сопротивление R можно найти по следующей формуле: 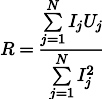
Этот результат несколько менее очевиден, чем простое среднее всех измерений.
Обратите внимание, что если мы сделаем сто измерений в районе одного ампера, и одно измерение в районе килоампера, то предыдущие сто измерений практически не окажут влияния на результат. Давайте запомним этот факт, он нам пригодится в следующей статье.
Пример четвертый: возвращение к методу наименьших квадратов Вы, наверное, уже заметили, что в последних двух примерах максимизация логарифмического правдоподобия эквивалентна минимизации суммы квадратов ошибки оценки.
Давайте посмотрим на другой пример.
Возьмем калибровку безмена с помощью эталонных гирь.
Имея N стандартных гирь массой xj, повесим их на безмене и измерим длину пружины, получим N длин пружины yj: 
Закон Гука говорит нам, что растяжение пружины линейно зависит от приложенной силы, и эта сила включает в себя вес грузов и вес самой пружины.
Пусть жесткость пружины является параметром а , а растяжение пружины под собственным весом – параметр b. Тогда мы можем записать выражение для вероятности наших измерений следующим образом (все еще в рамках гипотезы о гауссовском шуме измерений): 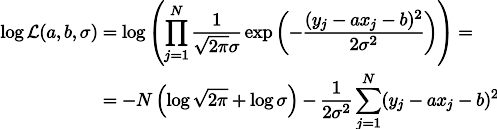
Максимизация правдоподобия L эквивалентна минимизации суммы квадратов ошибок оценки, то есть мы можем искать минимум функции S, определяемой следующим образом: 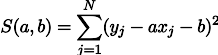
Другими словами, мы ищем линию, минимизирующую сумму квадратов длин зеленых отрезков: 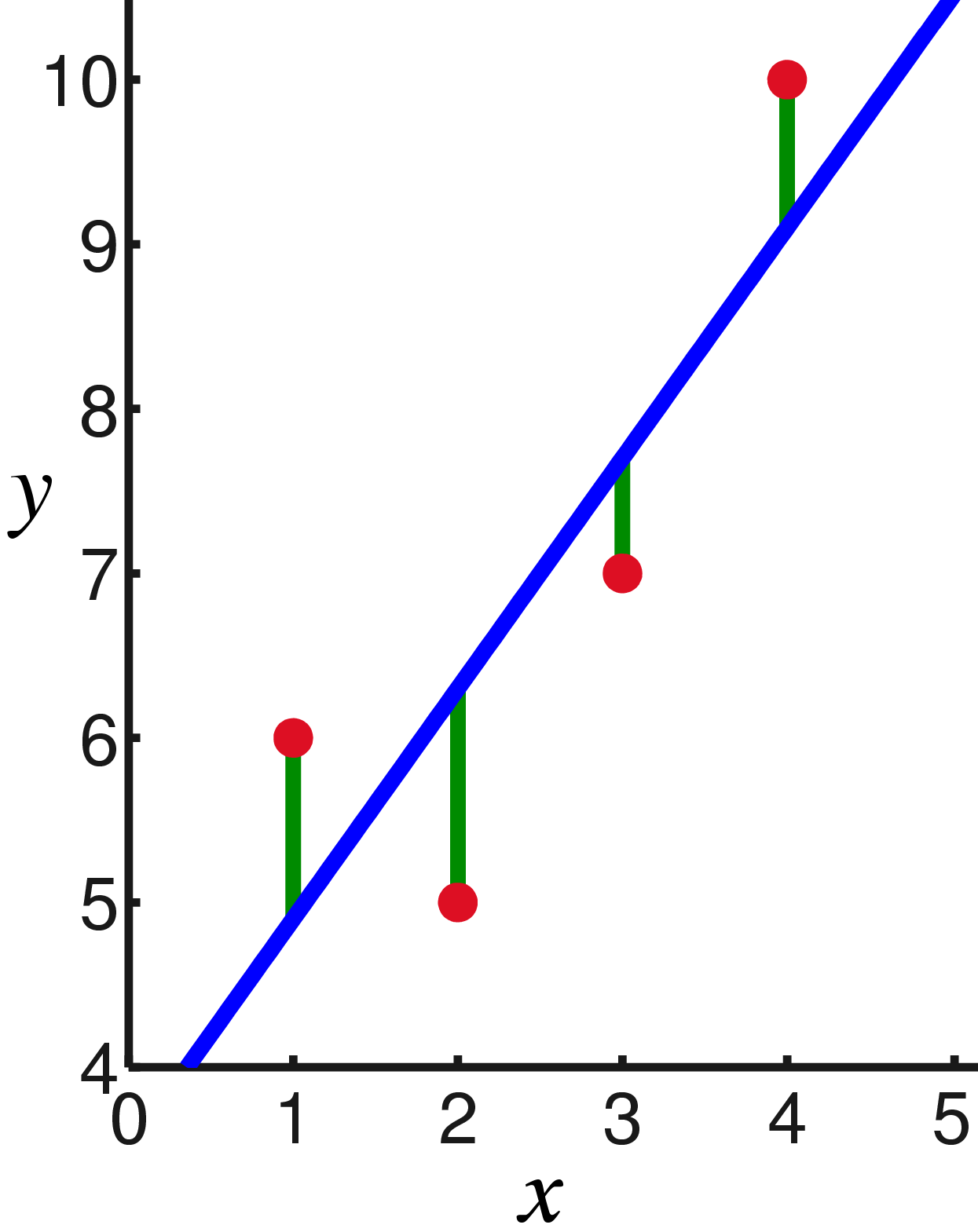
Ну тогда никаких сюрпризов, приравняем частные производные нулю: 
Получим систему двух линейных уравнений с двумя неизвестными: 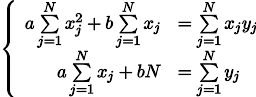
Вспоминаем седьмой класс школы и выписываем решение: 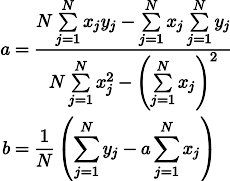
Заключение
Методы наименьших квадратов представляют собой особый случай максимизации правдоподобия для случаев, когда плотность вероятности является гауссовой.
В случае, когда плотность (вообще) не является гауссовой, OLS дает оценку, которая отличается от оценки MLE (оценка максимального сходства).
Кстати, в свое время Гаусс выдвинул гипотезу, что распределение не имеет значения, важна только независимость тестов.
Как видно из этой статьи, чем дальше в лес, тем громоздче становятся аналитические решения этой задачи.
Ну мы не в восемнадцатом веке, у нас есть компьютеры! В следующий раз, когда мы увидим геометрический, а затем и программный подход к задаче МНК, оставайтесь на верном пути.
Теги: #математика #Алгоритмы #программирование #C++ #математика на пальцах #математическое моделирование #геометрия для пятого класса #геометрия для пятого класса #LSM #математика для программистов #наименьшие квадраты

-
Люблю Программиста
19 Oct, 24 -
Livejournal -> Иван Засурский Сварился
19 Oct, 24


