Угадывание Наименьшего Уникального Натурального Числа (Случай Трёх И Четырёх Игроков)

Привет, Хабрахабр! Не так давно где-то на просторах одной соцсети я видел такую игру: игроки отправляют хосту (назовем его так) целое положительное число (игроки не знают номеров друг друга), тот, кто отправил наименьшее уникальное число выигрывает. Например, если играют 7 игроков и они прислали номера 5, 4, 2, 1, 1, 2, 6 , побеждает игрок, отправивший номер 4 .

Я жутко заинтересовался тем, как «правильно» играть в эту игру, но оказалось, что четкого решения для этого не существует. н Если здесь есть игроки, то это достаточно сложно и запутанно, поэтому рассмотрим конкретные случаи для 3 и 4 игроков.

Случай трех игроков

Выберите из {1, 2, 3} Итак, начнем.

Для начала введем ограничение: пусть игроки выбирают номера только из {1, 2, 3} (тогда будет проще и нагляднее перейти к выбору любого натурального числа).

Что мы сейчас попробуем сделать: найти такие смешанная стратегия

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

что если бы все игроки придерживались заданной стратегии, никто не смог бы увеличить свои шансы на победу, изменив стратегию (эта штука, кстати, называется равновесие по Нэшу ).

То есть, чтобы каждый игрок с вероятностью

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

выбрал номер 1 , с вероятностью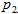

- число 2 и с вероятностью

– 3 , и каждому игроку было бы невыгодно отклоняться от этих вероятностей.

Предположим, что игроки 2 И 3 использовать эти вероятности, и игрок 1 решил увеличить свои шансы на победу и теперь использует стратегию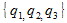

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

.

Чтобы выиграть, он должен выбрать номер 1 (а остальные игроки должны выбрать либо 2 , или оба 3 , или один 2 , а второй - 3 ), число 2 (остальные должны выбрать или и то, и другое 1 , или оба 3 ), или 3 (в этом случае остальные должны или оба выбрать 1 или выберите оба 2 ).

Таким образом, конечная вероятность выигрыша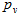

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

можно выразить как сумму этих трех вероятностей: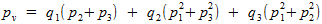

(1).

Не забываем также, что сумма всех вероятностей в конечном итоге равна единице, т.е.

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

(*).

Итак, игроку 1 вам нужно попытаться увеличить вероятность выигрыша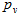

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

, но у нас есть ограничение (*).

Славный приходит на помощь Метод множителей Лагранжа , который делает именно то, что нам нужно — находит локальные экстремумы функции (для нас это функция (1)) при существующих ограничениях на некоторые равенства (для нас это равенство (*)).

Уравнение Лагранжа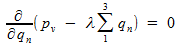

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

дает нам следующие уравнения: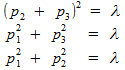

, который мы решаем, учитывая, конечно, равенство (*).

Получаем следующие вероятности: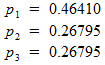

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

Готовый! Какой из этого вывод? Когда 3 игрока могут выбирать только из {1, 2, 3} , для каждого из них оптимальной стратегией будет следующая: примерно в половине случаев выбирают 1 , около четверти – выбирайте 2 , и примерно четверть – 3 .

Это будет равновесие Нэша.

Выберите любое натуральное число Что же произойдет, если мы удалим ограничения на множество, из которого игроки могут выбирать числа, и как нам найти равновесие Нэша для такой игры? Теперь, если игрок выбирает какое-то число я , он выиграет только в том случае, если все игроки выберут одинаковое число строго меньше я , или оба выберут число, каждое из которых строго больше я .

Таким образом, для каждого игрока вероятность выигрыша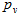

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

следующий:

.

Дифференцируя это уравнение, получаем бесконечную систему уравнений:

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

и ограничение

.

Эту проблему можно решить, но она довольно сложная, поэтому я просто дам ответ здесь:

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

.

Что все это значит? Если подставить в полученное уравнение конкретные числа, то для первых семи получим примерно следующие вероятности: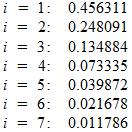

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

То есть равновесие Нэша будет представлять собой набор стратегий, в которых каждый игрок с вероятностью примерно 0,46 выбирает 1 , с вероятностью 0,25 – 2 , с вероятностью 0,13 – 3 , и так далее.

Случай четырёх игроков

Одна и та же игра вчетвером мало чем отличается от игры втроем.

В этом случае максимизируемая функция равна: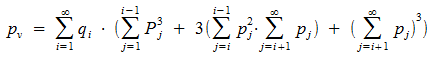

Угадывание наименьшего уникального натурального числа (случай трёх и четырёх игроков)

Что здесь:

Решение выглядит следующим образом:

Отсюда следует, что чаще всего вам придется выбирать цифры 1 И 2 , изредка - 3 , очень редко - 4 , и с числами больше четырех почти нет необходимости иметь дело.