
В первая часть мы познакомились с моделированием аплифта и узнали, что метод позволяет выбрать оптимальную стратегию общения с клиентом, а также рассмотрели особенности сбора данных для обучения модели и несколько основных алгоритмов.
Однако эти подходы не привели к прямой оптимизации подъема.
Поэтому в этой части мы разберем более сложные, но не менее интересные подходы.
Все уроки серии Часть 1: математический смысл, сбор обучающего набора, подъем модели Часть 2: модели поднятия (продолжение) Часть 3. Показатели подъема Содержание статьи Трансформация класса Преобразование классов (регрессия) Мультиклассовая модель Древовидные методы Заключение Источники
Трансформация класса
Подход к преобразованию классов, подход к преобразованию переменных класса, подход к возврату меток Довольно интересный и математически обоснованный подход к построению модели, представленный еще в 2012 году на ICML. [1] , который состоит из прогнозирования слегка измененной целевой переменной.
Где
- новая целевая переменная
й клиент
— целевая переменная
й клиент
— флаг двоичной связи: когда
—
Клиент-й попал в цель ( уход ) группа, в которой происходило общение; в
—
- клиент был помещен в диспетчерскую ( контроль ) группа, где не было общения.
Другими словами, новый класс равен 1, если мы знаем, что в конкретном наблюдении результат взаимодействия был бы таким же хорошим, как и в контрольной группе, если бы мы могли знать результат обеих групп: 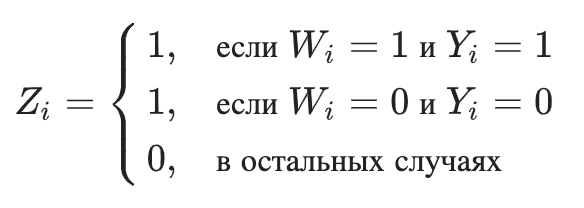

Опишем подробнее, какова вероятность новой целевой переменной: 
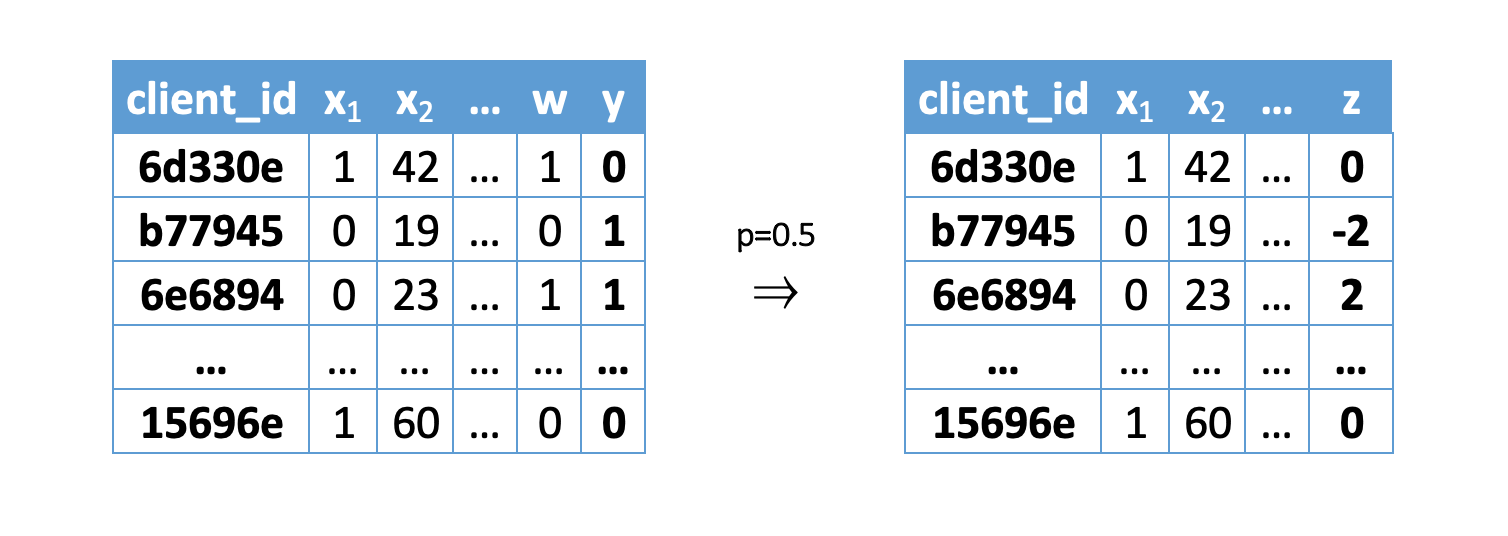
В первая часть В статье мы обсудили, что обучающая выборка для моделирования подъема собирается на основе рандомизированного разделения части клиентской базы на целевую и контрольную группы.
Поэтому общение
не может зависеть от особенностей клиента
.
Учитывая это, мы имеем:
Мы получаем: 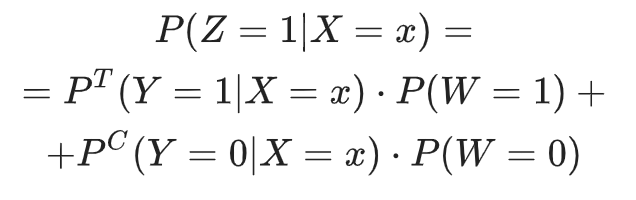
Давайте также предположим, что
, т.е.
в ходе эксперимента контрольная и целевая группы были разделены в равных пропорциях.
Тогда мы получим следующее: 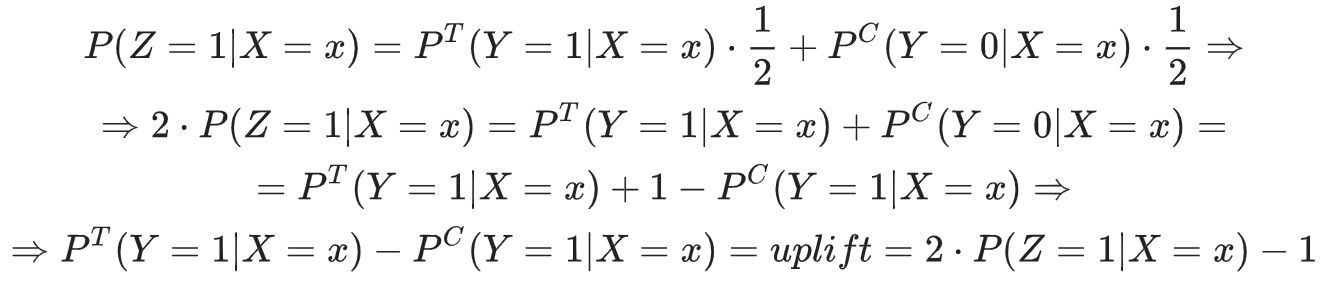
Таким образом, удвоив прогноз новой цели и вычтя из него единицу, мы получим значение самого подъема, т.е.
Исходя из предположения, описанного выше:
, этот подход следует использовать только в тех случаях, когда количество клиентов, с которыми мы общались, равно количеству клиентов, с которыми не было общения.
Трансформация класса (регрессия)
Преобразованный результат Предыдущий тип преобразования классов имеет серьезные ограничения: целевая переменнаяможет быть только бинарным, а контрольная и целевая группы должны быть распределены в равных пропорциях.
Давайте рассмотрим более общий подход из [2] , который не имеет таких ограничений.
Преобразуйте исходную целевую переменную
по следующей формуле:
Где
- новая целевая переменная для
й клиент
— флаг связи для
клиент
— показатель склонности или вероятность быть отнесенным к целевой группе:
Здесь важно отметить, что можно оценить
как доля объектов с
в образце.
Или используйте метод из [3] , который предлагает оценить
как функция
, обучив классификатор на имеющихся данных
и принимая вектор флага связи в качестве целевой переменной
.
После применения формулы мы получаем новую целевую переменную
и мы можем обучить модель регрессии с функционалом ошибок
.
Поскольку именно при применении MSE прогнозы модели представляют собой условное математическое ожидание целевой переменной.
Покажем, что условное математическое ожидание преобразованной цели
и есть желаемый причинный эффект от первая часть статьи:
Напомним также, что наблюдаемую целевую переменную можно представить как: 
Где
- потенциальные реакции для всех
-й объект в зависимости от значения
, который мы хотели бы (но не можем) наблюдать одновременно.
Перепишем формулу преобразования с учетом этого:
Затем: 
С каких это пор случайным образом разделены на целевую и контрольную группы
не должно зависеть от
, Что:
Мы обнаружили, что преобразованная целевая переменная позволяет нам оценить прирост: 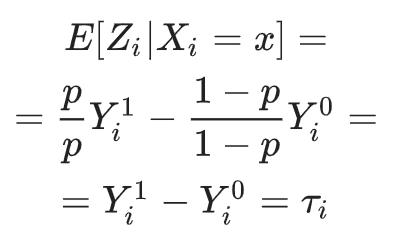
Мультиклассовая модель
Обобщенный метод Лай Итак, как мы можем взаимодействовать с клиентами?и понаблюдай за их реакцией
, то разделим их на 4 непересекающихся класса:
- Клиент выполнил целевое действие и мы с ним не общались( Ответчик управления – CR ):
- Клиент не выполнил целевое действие и мы с ним не общались( Контрольный не ответивший - CN ):
- Клиент выполнил целевое действие и мы с ним пообщались( Респондент, получивший лечение – TR ):
- Клиент не выполнил целевое действие и мы с ним связались( Пациент, не ответивший на лечение - TN ):

Фотография взята и адаптирована из [4] Попробуем разобраться, как связаны между собой выделенные выше 4 класса и типа клиентов.
первая часть , который мы хотим найти ( не беспокой, потерялся, верный, уговорил ).
Их главное отличие состоит в том, что классы ЧР, Китай, ТР, Теннесси мы можем наблюдать непосредственно по их реакции на общение, но не можем наблюдать за типами клиентов.
При этом они взаимосвязаны: каждый из четырех классов может содержать одновременно 2 типа клиентов.
- Поскольку мы не знаем, выполнили бы ЧР клиент – это целевое действие, находящееся под нашим влиянием, то речь идет либо о просьба не беспокоить , или чтобы лояльный клиенты.
Проводя аналогичные рассуждения, рассмотрим остальные классы:
- среди Китай клиенты могут быть такими потерянный , так убежденный типы клиентов
- Среди ТР клиенты могут быть такими убежденный , так лояльный типы клиентов
- Среди ТН клиенты могут быть такими просьба не беспокоить , так потерянный типы клиентов
Тогда подъем можно рассчитать следующим образом:
Суммируем вероятности принадлежности к классу
И
, поскольку они содержат тип убежденный , который мы хотим найти, и вычтем вероятности принадлежности к классу
И
, поскольку они содержат тип просьба не беспокоить , чего мне наоборот хотелось бы избежать.
Когда выборки очень несбалансированы по размеру, предлагается рассчитывать подъем следующим образом:
Где
— доля клиентов в тестовой группе,
— доля клиентов в контрольной группе,
.
Нормализация необходима, когда целевая группа мала по сравнению с контрольной группой, поскольку в этом случае доля ТР И ТН Клиентов тоже будет мало.
Древовидные методы
Деревья решений для моделирования поднятий, Причинные деревья Стоит отметить, что предыдущие способы имеют следующие недостатки:- В методах с двумя моделями при расчете итогового прогноза учитываются результаты двух моделей, то есть суммируются их ошибки;
- Если для обучения будут использоваться принципиально разные модели или характер данных целевой и контрольной групп будет сильно различаться, то может потребоваться калибровка прогнозов модели;
- Поскольку многие методы прогнозируют рост косвенно, модели могут упускать из виду тонкие различия между целевой и контрольной группами.
Например, авторы статьи [5] предлагают использовать деревья решений с другим критерием разделения.
Дерево строится таким образом, чтобы максимизировать расстояние (расхождение) между распределениями целевой переменной y контроль И цель группы.
Формально для каждого раздела это можно записать так:
Где
— распределение целевой переменной в контроль И цель группы
— расхождение (расхождение) между двумя распределениями
Существует несколько типов дивергенции D, которые используются для решения этой задачи:
- Расхождение Кульбака – Лейблера:
- Евклидово расстояние:
- Дивергенция хи-квадрат:
Если окажется, что в вершине при разбиении остаются объекты одной группы (управляющей или целевой), то дивергенция сводится к стандартному критерию для деревьев (КЛ-дивергенция - к критерию энтропии, евклидову расстоянию и хи- квадрат – к критерию Джини).
Еще одним важным условием разбиения является минимизация разницы между количеством объектов, попадающих в левую и правую дочерние вершины.
Слева на картинке пример плохого разбиения, когда высокое значение подъема в левой дочерней вершине достигается за счет того, что в нее попали только 30 объектов из 1000. 
Фотография взята и адаптирована из [7]
Для контроля количества объектов в разбиении можно использовать формулу взвешенной дивергенции (после разделения):
Где
И
— количество объектов, попадающих в левую и правую дочернюю вершину соответственно
— распределение целевой переменной в цель И контроль группа для левых и правых дочерних вершин
После реализации дерева с новым критерием расщепления вы можете использовать этот алгоритм как базовый в ансамблях, например, в случайном лесу или градиентном бустинге, а также применять стандартные для деревьев методы борьбы с переобучением, такие как обрезка или ранняя остановка) .
Заключение
Серия обзорных статей не охватывает все подходы к прогнозированию подъема, но охватывает наиболее популярные и интересные для нас.На сегодняшний день не существует идеального метода, который на основе разных данных и на протяжении длительного периода времени превосходил бы по качеству другие.
Этот факт мотивирует исследователей разрабатывать новые подходы (например, интересная статья 2019 года об использовании бандитов для решения этой проблемы).
[8] ).
В будущем мы планируем рассмотреть показатели качества для оценки прогнозируемого роста.
Моделирование Uplift используется не только для маркетинговых задач, но и в медицине, политике, экономике и других сферах.
То есть, когда поведение объектов может измениться под каким-то контролируемым воздействием, этот подход может быть предпочтительнее других.
Статья написана в соавторстве с Максимом Шевченко ( Макс-ш )
Источники
- [1] Мацей Ясковский и Шимон Ярошевич.
Моделирование подъема данных клинических испытаний.
Семинар ICML по анализу клинических данных, 2012 г.
- [2] Сьюзан Эти и Гвидо В.
Имбенс.
Методы машинного обучения для оценки гетерогенных причинных эффектов.
стат, 1050:5, 2015.
- [3] П.
Ричард Хан, Джаред С.
Мюррей и Карлос Карвалью.
Модели дерева байесовской регрессии для причинного вывода: регуляризация, смешивание и гетерогенные эффекты.
2019.
- [4] Кейн, К.
, В.
С.
Ю.
Ло и Дж.
Чжэн.
Майнинг для действительно отзывчивых и потенциальных клиентов с использованием моделирования True-Lift: сравнение новых и существующих методов.
Журнал маркетинговой аналитики 2 (4): 218–238. 2014.
- [5] Петр Жепаковский и Шимон Ярошевич.
Деревья решений для моделирования поднятия с помощью одиночного и несколько процедур.
Знания и информационные системы, 32(2):303–327, 2012.
- [6] Ян Чжао, Сяо Фан и Дэвид Симчи-Леви.
Моделирование подъема с использованием нескольких обработок и общих типов реакции.
В материалах Международной конференции SIAM по интеллектуальному анализу данных 2017 г.
, 588–596. СИАМ, 2017.
- [7] Воутер Вербеке, Барт Бэсенс, Кристиан Браво.
Бизнес-аналитика, ориентированная на прибыль: практическое руководство по преобразованию больших данных в добавленную стоимость.
- [8] Йерун Берревутс, Сэм Вербовен, Воутер Вербеке.
Оптимизация эффекта индивидуального лечения с помощью бандитов, 2019.

-
Прямая Линия С Тм. V4.0
19 Oct, 24 -
Большое Будущее Для Y Combinator
19 Oct, 24 -
Сегодня Wordpress Исполняется 7 Лет
19 Oct, 24


