Введение Эта статья является продолжением серия статей описание алгоритмов, лежащих в основе Синет — фреймворк для запуска предварительно обученных нейронных сетей на ЦП.
Если посмотреть на распределение процессорного времени, затрачиваемого на прямое распространение сигнала в нейронных сетях, то окажется, что зачастую более 90% общего времени тратится на сверточные слои.
Поэтому, если мы хотим получить быстрый алгоритм для нейронной сети, нам нужен, прежде всего, быстрый алгоритм для сверточного слоя.
В этой статье я хочу описать методы оптимизации прямого распространения сигнала в сверточном слое.
Более того, хотелось бы начать с наиболее широко используемых методов, основанных на умножении матриц.
Постараюсь изложить изложение в максимально доступной форме, чтобы статья была интересна не только специалистам (они и так все о ней знают), но и более широкому кругу читателей.
Я не претендую на полноту обзора, поэтому любые комментарии и дополнения приветствуются.
Параметры сверточного слоя
Описание хотелось бы начать с описания параметров, находящихся в сверточном слое.Эксперты могут смело пропустить этот раздел.
Размеры входного и выходного изображения
Прежде всего, сверточный слой характеризуется входным и выходным изображением, которые характеризуются следующими параметрами:- srcC/dstC — количество каналов во входном и выходном изображениях.
Альтернативные обозначения: CD .
- srcH/dstH — высота входного и выходного изображения.
Альтернативное обозначение: ЧАС .
- источник/dstW — ширина входного и выходного изображения.
Альтернативное обозначение: Вт .
- партия - количество входных (выходных) изображений – слой может обрабатывать сразу целую партию изображений.
Альтернативное обозначение: Н .
Размеры ядра свертки
Операция свертки по существу представляет собой взвешенную сумму определенной окрестности данной точки изображения.
Размер ядра свертки характеризует размер этой окрестности и описывается двумя параметрами: 
- ядроY — высота ядра свертки.
Альтернативное обозначение: Да .
- ядроX — ширина ядра свертки.
Альтернативное обозначение: Икс .
Размеры 5х5 И 7х7 встречаются гораздо реже.
Иногда встречаются свертки больших размеров, а также свертки с ядром, отличным от квадратного, но это более экзотично.
Шаг свертки
Еще одним важным параметром является шаг свертки:
- шагY — шаг вертикальной свертки.
- шагX — шаг горизонтальной свертки.
Растяжение свертки
Ядро свертки можно растянуть (увеличив эффективный размер окна при сохранении количества операций), используя следующие параметры: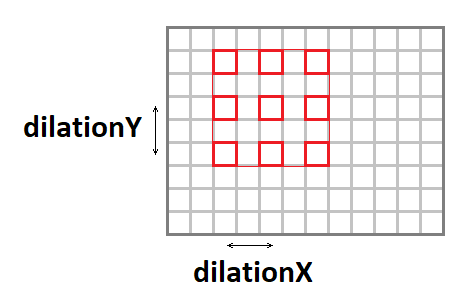
- расширениеY — вертикальное растяжение свертки.
- расширениеX — горизонтальное растяжение свертки.
Заполнение входного изображения
Если вы примените к изображению свертку с окном, отличным от единичного, выходное изображение будет меньше на величину ядро - 1 .Складка как будто «съедает» края.
Чтобы сохранить размер изображения, входное изображение часто дополняется по краям нулями.
За это отвечают еще четыре параметра: 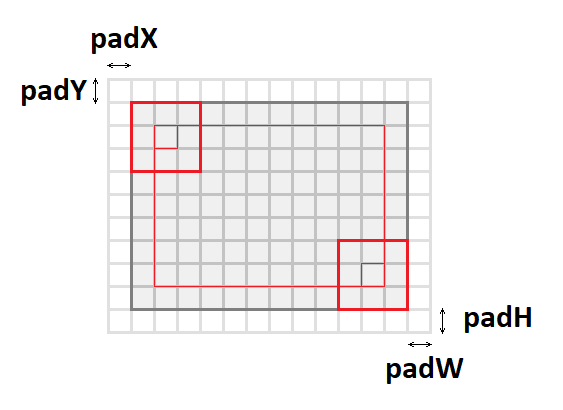
- пэдY/падX — передние вертикальные и горизонтальные отступы.
- PadH/padW — сзади вертикальные и горизонтальные отступы.
Группы каналов
Обычно каждый выходной канал представляет собой сумму сверток по всем входным каналам.Тем не менее, это не всегда так.
Возможно разделение входных и выходных каналов на группы; суммирование проводится только внутри групп: 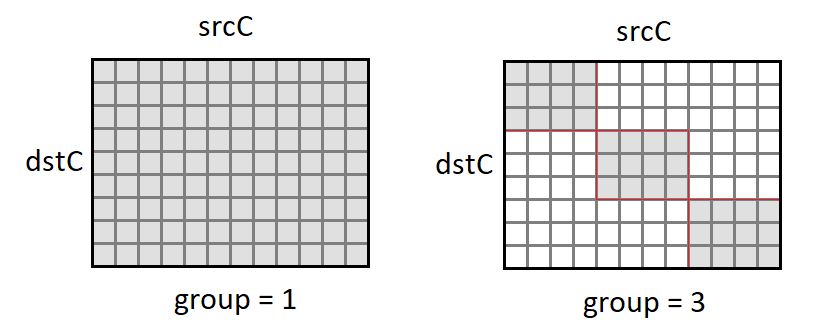
- группа — количество групп.
Смещение и функция активации
Хотя формально функция смещения и активации не входят в свертку, очень часто эти две операции следуют за сверточным слоем, поэтому их обычно тоже включают в него.Ввиду разнообразия возможных функций активации и их параметров я не буду здесь их подробно описывать.
Базовая реализация алгоритма
Для начала хотелось бы дать базовую реализацию алгоритма:В этой реализации я предполагал, что входное и выходное изображение имеют формат НЧВ :float relu(float value) { return value > 0 ? value : 0; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; dstC = dstC / group; srcC = srcC / group; for (int b = 0; b < batch; ++b) { for (int g = 0; g < group; ++g) { for (int dc = 0; dc < dstC; ++dc) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { float sum = 0; for (int sc = 0; sc < srcC; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) sum += src[(((b*group + g)*srcC + sc)*srcH + sy)*srcW + sx] * weight[(((g*dstC + dc)*srcC + sc)*kernelY + ky)*kernelX + kx]; } } } dst[(((b*group + g)*dstC + dc)*dstH + dy)*dstW + dx] = sum + bias[dc]; } } } } } }

веса свертки хранятся в формате DCYX , и наша функция активации РеЛУ .
В общем случае это не так, но для базовой реализации такие предположения вполне уместны — надо с чего-то начинать.
Имеем 8 вложенных циклов и общее количество операций: batch * kernelY * kernelX * srcC * dstH * dstW * dstC / group * 2,
в то время как объем данных на входе: batch * srcC * srcH * srcW,
и выходное изображение: batch * dstC * dstH * dstW,
и количество весовых коэффициентов: kernelY * kernelX * srcC * dstC / group.
Если группа << srcC (количество групп существенно меньше количества каналов), а также при достаточно больших параметрах srcC , источник , источник И dstC мы получаем классическую вычислительную задачу, когда количество вычислений значительно превышает количество входных и выходных данных.
Те.
Операция свертки при правильной реализации должна опираться на вычислительные ресурсы процессора, а не на пропускную способность памяти.
Осталось найти эту реализацию.
Сведение задачи к умножению матриц
Основная операция свертки — получение взвешенной суммы, веса которой одинаковы для всех точек выходного изображения.
Если мы изменим порядок входного изображения следующим образом: void im2col(const float * src, int srcC, int srcH, int srcW,
int kernelY, int kernelX, int dilationY, int dilationX,
int strideY, int strideX, int padY, int padX, int padH, int padW, float * buf)
{
int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1;
int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1;
for (int sc = 0; sc < srcC; ++sc)
{
for (int ky = 0; ky < kernelY; ky++)
{
for (int kx = 0; kx < kernelX; kx++)
{
for (int dy = 0; dy < dstH; ++dy)
{
for (int dx = 0; dx < dstW; ++dx)
{
int sy = dy * strideY + ky * dilationY - padY;
int sx = dx * strideX + kx * dilationX - padX;
if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW)
*buf++ = src[(sc*srcH + sy)*srcW + sx];
else
*buf++ = 0;
}
}
}
}
}
}
Тогда мы отойдём от формата исходник - источник - источник мы перейдем к формату srcC - kernelY - kernelX - dstH - dstW .
На рисунке ниже показано, как преобразуется изображение с отступами.
1 и ядро 3х3 : 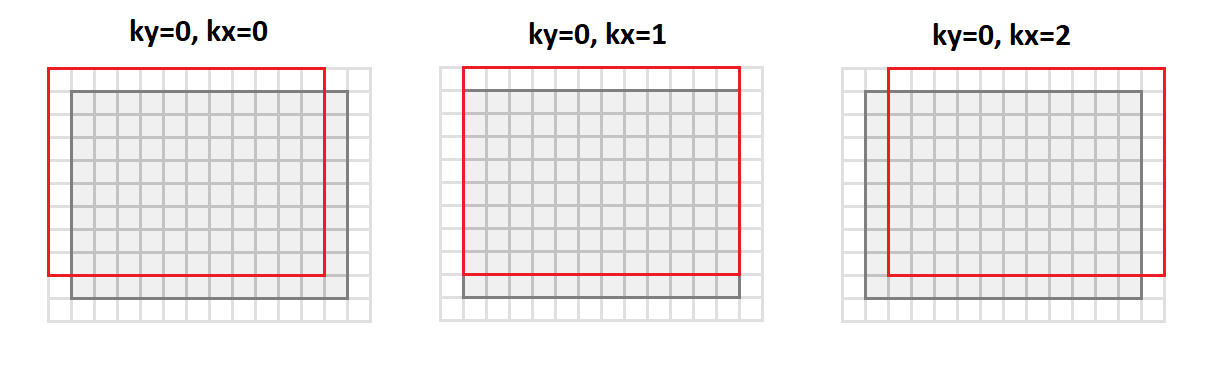
В этом случае все точки в окрестности изображения, необходимые для операции свертки, выстраиваются по столбцам результирующей матрицы (отсюда и ее название – я возраст к столбец гмнс).
Новое представление входного изображения интересно тем, что теперь операция свертки сведена к умножению матриц: 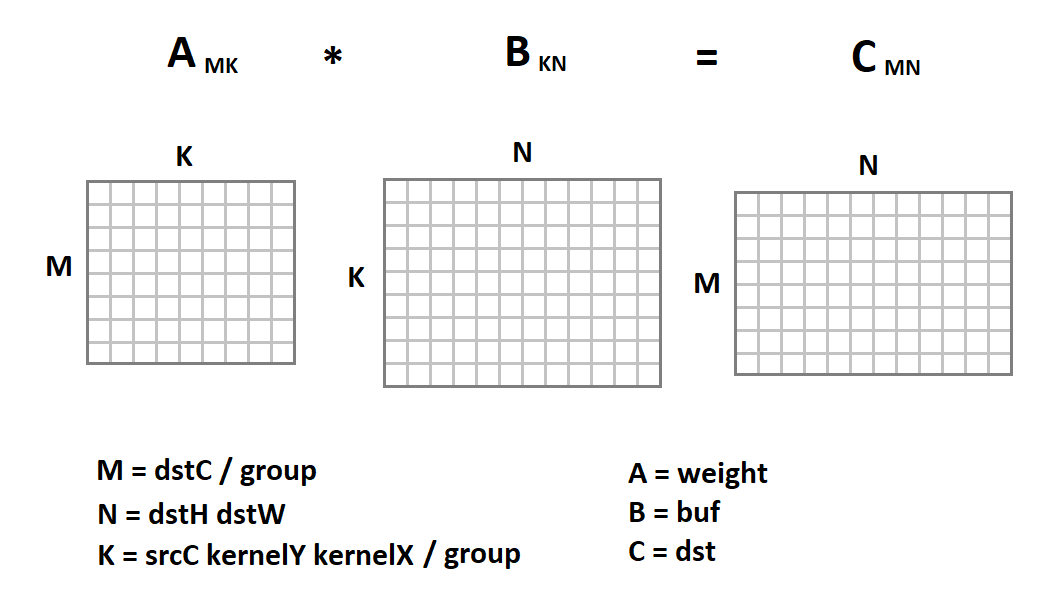
Код свертки теперь будет выглядеть так: void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda,
float beta, const float * B, int ldb, float * C, int ldc)
{
for (int i = 0; i < M; ++i)
{
for (int j = 0; j < N; ++j)
{
C[i*ldc + j] = beta;
for (int k = 0; k < K; ++k)
C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j];
}
}
}
void convolution(const float * src, int batch, int srcC, int srcH, int srcW,
int kernelY, int kernelX, int dilationY, int dilationX,
int strideY, int strideX, int padY, int padX, int padH, int padW, int group,
const float * weight, const float * bias, float * dst, int dstC, float * buf)
{
int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1;
int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1;
int M = dstC / group;
int N = dstH * dstW;
int K = srcC * kernelY * kernelX / group;
for (int b = 0; b < batch; ++b)
{
im2col(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationX,
strideY, strideX, padY, padX, padH, padW, buf);
for (int g = 0; g < group; ++g)
gemm_nn(M, N, K, 1, weight + M * K * g, K, 0, buf + N * K * g, N, dst + M * N * g, N);
for (int i = 0; i < dstC; ++i)
for (int j = 0; j < N; ++j)
dst[i*N+ j] = relu(dst[i*N + j] + bias[i]);
src += srcC*srcH*srcW;
dst += dstC*dstH*dstW;
}
}
Здесь тривиальная реализация умножения матриц приведена только в качестве примера.
Мы можем заменить его любой другой реализацией.
К счастью, умножение матриц — давно зарекомендовавшая себя операция, уже реализованная во многих библиотеках с очень высокой эффективностью (до 90% от теоретически возможной производительности ЦП).
На тему того, как достигается такая эффективность, у меня даже есть отдельная статья .
Использование матричного умножения для формата NHWC
Наряду с форматом НЧВ , в машинном обучении часто используется формат НХВК :
Например, отметим, что НХВК - это родной формат Тензорный поток .
Примечательно, что для этого формата операцию свертки также можно свести к умножению матриц.
Для этого из формата источник - источник - источник конвертировать исходное изображение в формат dstH - dstW - kernelY - kernelX - srcC используя функцию im2row : void im2row(const float * src, int srcC, int srcH, int srcW,
int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX,
int padY, int padX, int padH, int padW, int group, float * buf)
{
int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1;
int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1;
for (int g = 0; g < group; ++g)
{
for (int dy = 0; dy < dstH; ++dy)
{
for (int dx = 0; dx < dstW; ++dx)
{
for (int ky = 0; ky < kernelY; ky++)
{
for (int kx = 0; kx < kernelX; kx++)
{
int sy = dy * strideY + ky * dilationY - padY;
int sx = dx * strideX + kx * dilationX - padX;
for (int sc = 0; sc < srcC/group; ++sc)
{
if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW)
*buf++ = src[(sy * srcW + sx)*srcC + sc];
else
*buf++ = 0;
}
}
}
}
}
src += srcC / group;
}
}
В этом случае все точки окрестности изображения, необходимые для операции свертки, выстраиваются по строкам результирующей матрицы (отсюда и ее название — я возраст к ряд с).
Нам также следует изменить формат хранения весов свертки с формата DCYX форматировать YXCD .
Теперь мы можем применить матричное умножение: 
В отличие от формата НЧВ , мы умножаем матрицу изображения на матрицу весов, а не наоборот. Ниже приведен код функции свертки: void convolution(const float * src, int batch, int srcC, int srcH, int srcW,
int kernelY, int kernelX, int dilationY, int dilationX,
int strideY, int strideX, int padY, int padX, int padH, int padW, int group,
const float * weight, const float * bias, float * dst, int dstC, float * buf)
{
int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1;
int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1;
int M = dstH * dstW;
int N = dstC / group;
int K = srcC * kernelY * kernelX / group;
for (int b = 0; b < batch; ++b)
{
im2row(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationX,
strideY, strideX, padY, padX, padH, padW, group, buf);
for (int g = 0; g < group; ++g)
gemm_nn(M, N, K, 1, buf + M * K * g, K, 0, weight + N * g, dstC, dst + N * g, dstC);
for (int i = 0; i < M; ++i)
for (int j = 0; j < dstC; ++j)
dst[i*dstC+ j] = relu(dst[i*dstC + j] + bias[j]);
src += srcC*srcH*srcW;
dst += dstC*dstH*dstW;
}
}
Преимущества и недостатки метода
Для начала хотелось бы перечислить преимущества такого подхода:- Этот метод имеет очень простую реализацию.
Не зря он используется практически во всех известных мне библиотеках.
- Эффективность метода во многих случаях очень высока: с нескольких процентов в базовом варианте мы достигаем более 80% теоретического максимума.
- Подход универсальный — у нас есть один код для всех возможных параметров сверточного слоя (а их довольно много!).
Поэтому этот метод часто работает в тех случаях, когда более эффективные (и, следовательно, более специализированные) подходы имеют ограничения.
- Этот подход работает для базовых форматов тензоров изображений — НЧВ И НХВК .
- К сожалению, стандартное умножение матриц эффективно при условии, что значения параметров М, Н, К достаточно велики и, кроме того, представляют собой величины примерно одного порядка (эффективность основана на том, что необходимое количество вычислений ~О(Н^3) , а требуемая пропускная способность памяти ~О(Н^2) ).
Следовательно, если какой-либо из параметров М, Н, К мала, то эффективность метода резко падает.
- Метод требует преобразования входных данных.
И это далеко не бесплатная операция.
Пренебрегать им можно лишь в том случае, если имеется достаточно большое К .
А если еще учесть, что внутри стандартного умножения матриц происходит еще и внутреннее преобразование входных данных, то ситуация становится еще печальнее.
- На основании того, что K = srcC * kernelY * kernelX / группа Особенно низка эффективность метода для входных сверточных слоев.
И для глубокая свертка Матричный метод в целом проигрывает тривиальной реализации.
- Метод требует дополнительной обработки выходных данных операции сдвига и расчета функции активации.
- Существуют более эффективные математические методы расчета свертки, требующие меньшего количества операций.
выводы
Метод расчета свертки, основанный на умножении матриц, прост в реализации и имеет высокую эффективность.К сожалению, он не универсален.
Для ряда частных случаев существуют более быстрые подходы, описание которых хотелось бы отложить до следующих статей этой статьи.
ряд .
Жду отзывов и комментариев читателей.
Надеюсь, вам было интересно! P.S. Этот и другие подходы были реализованы мной в Структура свертки в библиотеке Симд .
Эта основа лежит в основе Синет — фреймворк для запуска предварительно обученных нейронных сетей на ЦП.
Теги: #Машинное обучение #Алгоритмы #C++ #Обработка изображений #simd #сверточный слой #умножение матриц #Кэш процессора
-
Оптимальная Мобильная Ос Для Хабрачеловека
19 Oct, 24 -
Предотвращение Sql-Инъекций
19 Oct, 24


