Это третья статья из серии об использовании R для статистического анализа данных, в которой рассматривается представление и тестирование количественных данных.
Вы узнаете, как быстро и четко представлять данные, а также как использовать t-тест в R. Часть 1: Бинарная классификация Часть 2: Качественный анализ данных
Идти!
Для начала хочу еще раз привести схему из предыдущей статьи: 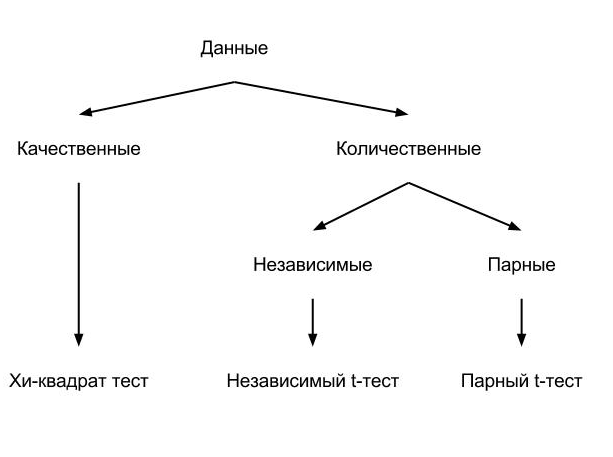
"
Парные данные отличаются тем, что данные для тестовых групп были получены от одних и тех же объектов.
Приложения для t-теста: влияние любого фактора на изменение продаж/скорости приложения/срока жизни устройства, сравнение двух групп людей по продуктивности.
Если групп несколько, то для анализа используются модели ANOVA (ANOVA — дисперсионный анализ), о которых пойдет речь в следующих статьях.
Представление данных перед анализом
Начнем с того, как представить данные.Я использую имеющийся у меня файл одного медицинского теста, который я использовал во время учебы.
Я опишу это кратко.
Люди из двух групп — основной и контрольной — выполнили несколько упражнений.
До и после занятий измеряли их физиологические параметры.
Попробуем проанализировать пульс и объем форсированного выдоха.
Помимо t-тестов, я расширю предыдущую статью и покажу, как получить качественные данные из чисел.
Так:
Мы генерируем дополнительный столбец с разницей в частоте сердечных сокращений до и после, а также дополнительный столбец качественных данных для объема форсированного выдоха, который можно проверить с помощью теста хи-квадрат. Последнее делается с помощью функции обрезки.tab <- read.csv(file="data1.csv", header=TRUE, sep=",", dec=".") attach(tab) tab tab <- cbind(tab, pulsediff=pulse2-pulse1, FEVcut2.5=cut(FEV1_1, c(0,2.5,max(FEV1_1)+0.1))) str(tab) detach(tab) attach(tab)
Мы задаем данные и вырезаем в них точки.
На выходе: 
"
Давайте двигаться дальше.
Рассчитаем средние значения и стандартные отклонения и построим наглядные графики.
mean(pulsediff[group==0], na.rm=T)
mean(pulsediff[group==1], na.rm=T)
sd(pulsediff[group==0], na.rm=T)
sd(pulsediff[group==1], na.rm=T)
boxplot(pulsediff~group,
main="Distribution of pulse difference stratified by group",
names=c("control-group", "exercise-group"),
ylab="pulse difference")
Из важного момента, который я хочу отметить, na.rm=T .
Если ваши данные содержат пустые ячейки, R удалит их автоматически.
В противном случае вы получите сообщение об ошибке.
Бокс-сюжет — очень хороший метод визуализации образца.
Он показывает максимум и минимум, среднее значение, а также 25- и 75-процентные квантили вероятности.

Теперь поговорим о разнице между парными и независимыми данными со статистической точки зрения.
В случае независимых данных для анализа используется следующий доверительный интервал: 
Среднее значение здесь представляет собой разницу между средними значениями каждой выборки, а стандартное отклонение рассчитывается с использованием специальной формулы для расчета разницы.
В случае парных данных мы вычитаем значения попарно и получаем новую выборку, из которой находим среднее значение и стандартное отклонение.
Доверительный интервал: 
Использование тестов в R
#Paired data
#approach 1:
t.test(pulsediff[group==1])
t.test(pulsediff[group==0])
#approach 2:
t.test(pulse1[group==1], pulse2[group==1], paired=T)
t.test(pulse1[group==0], pulse2[group==0], paired=T)
Здесь мы посмотрим на разницу между частотой сердечных сокращений до и после в одной группе.
Вы можете использовать t.test двумя способами: отправив ему разницу или два массива данных.

"
Выводы: в группе 0 нет разницы до и после, в группе 1 разница есть, т.к.
р-значение много менее 5% .
#Unpaired data
t.test(pulsediff~group)
Здесь мы анализируем разницу между группами.
Данные независимы.
Строго говоря, R использует тест Уэлча, который немного отличается от обычного t-теста.
Критерий Уэлча более точен и сходится при большом размере выборки.

"
Выводы: разница между группами существенная, т.к.
значение р много менее 5% .
#Descriptive analysis:
library(prettyR)
str(FEVcut2.5)
str(sex)
xtab(sex~FEVcut2.5, data=tab)
#Inferential analysis:
chisq.test(table(sex, FEVcut2.5), correct=F)
#ADD:
chisq.test(table(sex, FEVcut2.5))
fisher.test(table(sex, FEVcut2.5))
Здесь мы сравниваем объем форсированного выдоха у мужчин и женщин.
Таблица (из R gui, в RStudio лично у меня таблицы немного некорректно отображаются): 
"
Полученные результаты: 
"
Здесь мы применили целых три теста, увеличивая сложность и точность.
Я еще раз рекомендую использовать тест Фишера, но имейте это в виду.
Выводы: Тесты дали разные результаты, но значение p по-прежнему очень мало.
Группы отличаются друг от друга.
Полученные результаты
Итак, сегодня мы рассмотрели примеры использования тестов.Этой информации достаточно для проведения достаточно качественных статистических исследований.
Эти методы можно применять в любой сфере.
Их использование убережет вас от ошибок, позволит объективно оценить свою работу и предоставить другим людям объективно достоверную информацию.
Есть еще несколько тем, которые я хочу затронуть, касающихся оценки необходимого размера выборки, доказательства равенства случайных величин и моделей ANOVA. Теги: #r #статистика #анализ данных #математика #статистические тесты #статистический анализ #математика #r

-
Как Подключить Скрипт К Стороннему Сайту
19 Oct, 24 -
Обзор Систем Онлайн-Консультирования
19 Oct, 24 -
Решение Картинки Из Твиттера Intel
19 Oct, 24 -
Эмулятор Chip-8 Для Gtk+ На Практике
19 Oct, 24


