ДРОД – очень необычная логическая игра.
Его основные особенности:
- Шаг за шагом.
В отличие от супаплекса, реакция не имеет значения.
- Определение.
Здесь нет элемента случайности; любую позицию можно рассчитать в уме, хотя обычно это не так-то просто сделать.
- Большое концептуальное разнообразие головоломок.
Благодаря этому игра надоедает гораздо медленнее, чем, например, судоку.
- Приключенческий сеттинг, придающий процессу смысл (в основной миссии мы делаем виртуальный мир ДРОДа немного чище).
Каждый ход вы можете либо пойти в одну из 8 соседних ячеек, либо повернуть меч, либо подождать.
После чего выжившие монстры по очереди идут. Если они могут занять клетку, на которой стоит игрок, они проигрывают и возвращаются в начало комнаты.
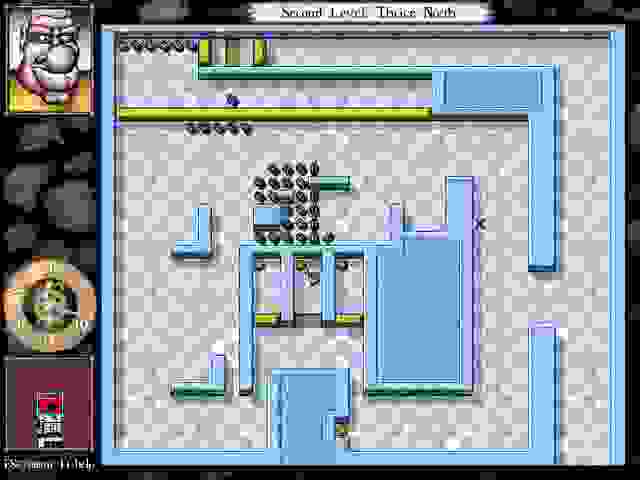
Дополнительный интерес к игре придает таблица рекордов скорости (по количеству ходов) прохождения комнат. Это наша цель.
Но как можно применить компьютер к игре с концептуально разными головоломками и астрономическим количеством вариантов (в любой момент времени у нас есть 11 возможных ходов, а общее количество возможных состояний комнаты гораздо больше, чем в шахматах)?! Выход один – передать интеллектуальную часть задачи человеку, а расчетную часть (оптимизация решения по количеству ходов) – компьютеру.
Когда я приступил к выполнению задачи, я не ожидал никакого успеха.
В конце концов, комнаты в ДРОДе могут быть настолько сложными, что обдумывать их придется целый месяц.
Но все же я решил рискнуть.
Первое, что нам пришлось сделать, это упростить игровую модель, чтобы увеличить скорость симуляции ходов.
Из-за такого упрощения многие элементы приходится заменять либо эквивалентными в данной ситуации, либо аналогичными, либо оптимизировать решение только части головоломки.
Во-вторых, пришлось придумать компактную схему хранения состояния комнаты и в дополнение к ней использовать архиватор, иначе место на винчестере исчезает очень быстро, а скорость ввода-вывода заметно влияет на производительность.
После чего был написан следующий простой перебор:
- Делаем все возможные ходы из текущего набора позиций.
В этом случае идентичные позиции удаляются с помощью хеш-таблицы.
- Выбираем N лучших вариантов по некоторой оценочной функции.
(из-за дискретности значений оценочной функции они могут быть немного меньше N)
- Распечатываем лучший вариант и возвращаемся к первому шагу.
Каково же было мое удивление, когда после запуска всего с N=100000 вариантов (напомню, это соответствует количеству вариантов примерно через 5 ходов, при типичной длине решения 300 ходов) после нескольких часов работы программа не заработала.
смог пройти только комнату (точнее ее основную часть, после чего добить оставшихся монстров проще простого), с чем я уже несколько дней безуспешно борюсь, но и сделал это почти в 2 раза быстрее чем лучшее человеческое решение для этой комнаты! В результате тандем «придуманная мною оценочная функция» + перебор смог пройти очень значительный процент комнат. Единственное, что могло этому помешать, — это неподдерживаемые элементы, помещения, в которых невозможно придумать сколько-нибудь разумную оценочную функцию, и лазейки (есть еще «грязь», у которой похожая проблема)… Трапдор — это квадрат, на который можно наступить только один раз.
Как только вы выйдете из него, трапдор падает вниз и образуется пустота.
Каждый трапдор удваивает количество вариантов, а учитывая, что обычно они заполняют целые области, ни 10^5, ни 10^8 вариантов не помогают. Программа начинает просчитывать множество по сути одинаковых вариантов, среди которых в один чудесный момент не появляется правильный.
Казалось бы, ситуация безнадежна.
Так я думал, пока мне не понадобилось отчаянно найти решение для такой комнаты.
Оказалось, что простая модификация алгоритма решила проблему.
Вместо выбора N лучших вариантов с точки зрения оценочной функции f, вам нужно выбрать N лучших вариантов с точки зрения значения random*exp(-const*f) (спасибо методу отжига за эту идею), где const определяется человеком, внимательно присмотревшись к потолку.
Собственно, при стремлении const к бесконечности мы получаем обычную схему выбора.
Однако в качестве цены новый метод требует более тщательного выбора оценочной функции (раньше было важно только упорядочение на множествах состояний, которое задается оценочной функцией f, а теперь важны сами значения ).
В нужном мне помещении такой подход позволил найти удачное решение.
Хотя следует признать, что общая проблема трапдоров остается нерешенной, так как зачастую имеет значение топология остальных трапдоров, которую невозможно выразить в виде оценочной функции, а использование случайности вредит вариантам решения, в которых степень разумности последствия не велики.
Теги: #Логические игры #Чулан

-
Вам Нужен Adobe Photoshop?
19 Oct, 24 -
Публикация Видео И Музыки На Mac Os X Lion
19 Oct, 24 -
Менеджер Http-Запросов В Unreal Engine
19 Oct, 24 -
Как Данные Передаются По Радио?
19 Oct, 24


