Непростые числа 
Автор статьи предлагает взглянуть на то, что представляют собой наборы простых чисел, если посмотреть на них геометрически.
Это не профессиональная работа, а простое любительское изучение каких-то интересных закономерностей.
Поэтому в статье не будет сложной математики, и мы не будем углубляться в ее дебри.
В общем, если вы не очень хорошо знакомы с простыми числами, их структурой и многовековыми исследованиями в области теории чисел, эта статья для вас.

Отдельно хочу подчеркнуть для квалифицированных математиков и тех читателей, которые считают себя одними из них: статья не является профессиональной работой.
Это иллюстрация некоторых свойств и закономерностей составных чисел исключительно для ясности и для того, чтобы подчеркнуть закономерности структуры, которые впоследствии можно выразить аналитически.
Читатель, вероятно, знает о многих проблемах, связанных с простыми числами.
Их место в множестве натуральных чисел неочевидно.
Большие простые числа найти трудно; требуется много усилий, чтобы проверить большое число на простое число.
Многие современные криптографические методы основаны на этой трудности.
Мы легко можем перемножить многозначные простые числа, но зная результат, найти исходные множители – очень сложная задача.
Существует множество методов оптимизации, которые намного быстрее простого перебора, но даже если оптимизация ускоряет поиск в 10 раз, достаточно увеличить число на 2 знака после запятой (т. е.
в 100 раз), чтобы замедлить поиск в 100 раз.
раз.
Это означает, что сложность алгоритма экспоненциальна, и поэтому, каким бы быстрым ни был суперкомпьютер, мы можем выбрать длину числа еще большей, чтобы потребовалось миллиард таких суперкомпьютеров.
Правда, стоит еще раз уточнить: находить простые числа для умножения тоже становится все сложнее.
Кстати, математики не нашли ни доказательства, ни опровержения того, что невозможно найти алгоритм факторизации, сложность которого не зависела бы экспоненциально от длины числа.
И доказывая или опровергая это, как полагают некоторые математики, можно в то же время решить математическую задачу, известную как гипотеза Римана.
За ее доказательство Математический институт Клея обещает миллион долларов.
Хотя может оказаться, что задача факторизации окажется полиномиальной, это не докажет и не опровергнет гипотезу Римана.
Числа отбрасывают тень? Поскольку мы не знаем закономерности, которая облегчила бы поиск простых чисел, может быть, давайте подробнее рассмотрим закономерности составных чисел? Говоря математическим языком, рассмотрим набор натуральных чисел, дополняющий набор простых чисел.
Идея составных чисел очень проста.
Давайте возьмем несколько натуральных чисел и перемножим их.
Таким образом, мы получаем составное число.
Мы можем легко найти бесконечность составных чисел, просто умножив n на 2. 
То же самое касается и умножения на 3. 
Дальше идет 4, но здесь новых чисел мы не найдем, все они уже равны 2n. Дальше идут 5n, затем 6n, которые мы уже нашли дважды, как 2n и 3n одновременно.
Это не увеличивает количество составных чисел, но наводит на мысль, что структура составных чисел определяется произведением простых чисел.
Но если пойти немного дальше, то мы обнаружим интересную закономерность: число 6 — это произведение 2 и 3. Это значит, что у нас будет множество составных чисел, удобно расположенных в таблице: 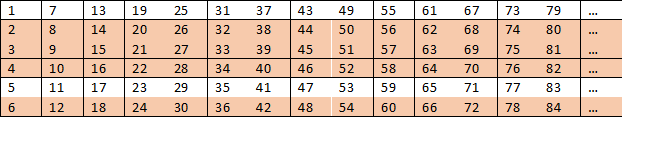
Глядя на таблицу, мы понимаем, что строки 2, 3, 4 и 6 никогда не могут содержать простые числа.
Это означает, что вероятность найти простое число не может превышать 2/6. Мы понимаем, что в цифрах эта вероятность еще меньше, но насколько?
Попробуем продолжить поиск удобной структуры составных чисел и для этого задумаемся, что означает 2х3=6? А что если взять за основу произведение 2х3х5? Получаем следующую интересную таблицу (чтобы она не занимала много места, уменьшим шрифт): 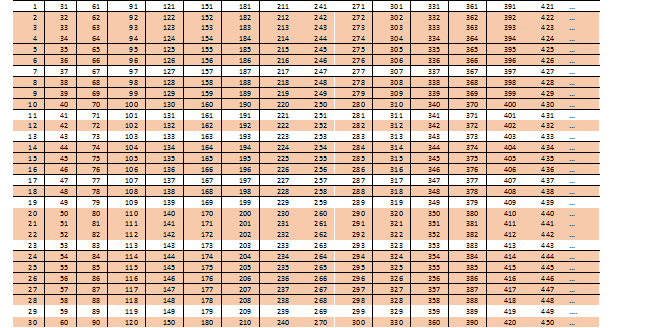
Мы видим, что:
— 15 строк вида 2n,
— 5 линий типа 3н (плюс 5 типа 6н уже учтены в 2н)
- и 2 строки вида 5н (еще три вида 10н уже вычеркнуты в числах 2н и одна 15н среди строк 3н)
не может содержать простые числа (мы этого и ожидали, верно?)
Осталось всего восемь строк вида 30n + i, где i = 1, 7, 11, 13, 17, 19, 23, 29. Если присмотреться, то можно увидеть в них симметрию.
1+29=7+23=11+19=13+17. Следовательно, компактно его можно записать как 30n +- i, где i = 1, 7, 11, 13,17. И мы понимаем, что вероятность найти произвольное простое число составляет не более 8/30. на 2/30 меньше.
Что дальше? Следуя логике, следующая таблица должна иметь 2x3x5x7=210 строк.
Еще дальше 210х11 = 2310, затем 2310х13 и так будем последовательно умножать простые числа, получая все большую и большую базу «строчной развертки», которая сохранит свою чередование.
Это выглядит так, как будто простые числа отбрасывают «тени» на бесконечность своих кратных, если их расположить в ряд по основанию числа, обозначим его P(i), равного последовательному произведению i простых чисел.
Можно заметить, что полоска строк, лежащая между первой и следующей, которая может содержать простые числа, растет по очень простому закону: если строк 6, то есть 2х3, то простые числа могут находиться в строке 5. , если 2х3х5, то начиная с 7 строки, что логично.
Таким образом, в матрице с числом строк 30 030 (2х3х5х7х11х13) после первой строки будет широкая полоса составных чисел, вплоть до строки, следующей за числом 17. А если взять матрицу с 9 699 690 строками (2х3х5х7х11х13х17х19 ), то полоска, где простых чисел нет, она растянется до 21 строки.
Характерно, что из-за симметрии внизу матрицы также будет 20 строк с исключительно составными числами.
Многомерные матрицы и гиперреалистичные фракталы? Но что это за произведения? 2х3 — прямоугольник площадью 6. 2х3х5 — это параллелепипед объёмом 30. И что дальше? 2х3х5х7 — гиперпараллелепипед в 4 измерениях, с гиперобъемом 210? А потом? 5 измерений, 6,.
Бесконечность? Только подумайте, что вы можете представить себе многомерный мир, в котором простые числа отбрасывают свою тень во всех измерениях.
Мы можем представить себе четыре и более измерений, спроецировав их на плоскость или в трехмерное пространство, например, развернув матрицу, как бы перекатывая многомерный гиперкуб от грани к грани и рассматривая полученные отпечатки на бумаге (а также получая отпечатки разделов).
Вот начальный край: 
А вот его развитие с обеих сторон: 
Очень повезло, что во всей правой гиперплоскости мы имеем исключительно составные числа.
Нам даже не придется туда ехать.
Можно посмотреть и на другой вид, вид сверху, но тогда мы пойдем в более интересном направлении.

Давайте теперь попробуем расширить картину в четвертое измерение, в том направлении, которое нас интересует, где мы можем найти простые числа: 
Здесь коричневым цветом обозначены числа вида mn, которые составлены из произведений чисел от 11 до 19 (ближайшее целое число меньше 210/11).
Особенность этих чисел в том, что они сами, не будучи простыми числами, не «отбрасывают тени» вглубь следующего измерения.
Как видим, средний слой развертки снова становится тривиальным — здесь и далее простых чисел нет. Но внешние края гиперпаллепипеда можно рассмотреть дальше.
Каждый столбец разлагается на матрицу 7х11, получаем по 5 таких матриц для каждого из трех слоев матрицы 3х5 (здесь показаны развертка одного столбца и фрагмент матрицы для второго столбца): 
Мы не будем углубляться в измерения на примере развертки; это было бы неразумно в рамках статьи.
В конце статьи вы можете посмотреть еще несколько иллюстраций.
Надеюсь, это исследование немного пробудило ваше воображение, и путешествие в мир комплексных и простых чисел вам понравилось и вы нашли его полезным.
Заключение Кроме того, автор хотел бы отметить, что он продолжает исследования этого метода.
Например, вопросы появления в более крупных матрицах произведений третьих, четвертых и последующих степеней чисел, которые добавляют все новые и новые простые числа в глубоких и объемных проекциях, как отбрасывая тень в последующие измерения, так и оставаясь «точечными».
включения.
Но, пожалуй, наибольший интерес представляет возможность дальнейшего уточнения оценки вероятности нахождения простых чисел.
Если мы посмотрим на матрицы, то увидим, как вероятность падает, начиная с 4/6, затем до 7/24 (или в среднем 11/30), затем 36/180 (или 47/210) и т.д. Кроме того, у автора есть алгоритм факторизации, оптимизация которого в многомерной матрице позволяет существенно ускорить его (но это не мешает ему иметь экспоненциальную степень сложности в зависимости от количества цифр факторизуемого числа).
Сам алгоритм по своей сути очень прост. Возьмите два последовательных нечетных числа, p и q, так, чтобы pq было близко к X (используется округление корня X до большего и меньшего нечетного числа, при условии, что X не является квадратом).
Сначала мы устраняем четность X (делим на 2, пока результат четный), получая коэффициент 2^K. Далее в цикле мы проверяем разницу между X и pq. Если он равен нулю, результат получен.
Если оно больше нуля, мы уменьшаем q на 2. Если оно меньше нуля, мы увеличиваем p на 2q. В цикле используется только сложение, поэтому алгоритм достаточно быстрый (зависит только от реализации функций для работы с BigInteger).
Однако у автора есть гипотеза, что шаг преобразования можно существенно увеличить без потери точности, если использовать базу кратности.
Любое число X находится между двумя последовательными P(i) и P(i+1), где P(i) — произведение первых i простых чисел, поэтому вы можете определить, к какому ребру ближе число X и каково диапазон свободы p и q в каждой из проекций) и тем самым расширить прямоугольник, образованный p и q, из одной плоскости в сечение гиперпараллелепипеда.
P.S. При чем здесь тайное общество ткачей, спросит читатель, которого привлекло оригинальное название? Читатель, возможно, помнит фильм «Особо опасен».
В этом году даже обещают продолжение.
В этом фильме ткацкий станок делает предсказания, раскладывая нити и узлы.
Посмотрите, как похоже это делают нити простых чисел.
В матрице 30х7: 
И кусок матрицы 210х11: 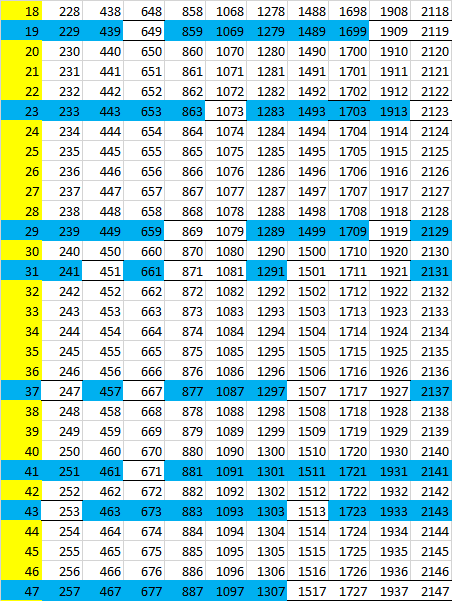
И компоненты этой машины управляются этими матричными перфокартами.
Сканирование матрицами 2x3: 
И еще, с матрицами 6x5: 
Теги: #простые числа #Факторизация #Особое мнение #многомерные матрицы #Криптография #Алгоритмы #математика

-
Я? Умный?
19 Oct, 24


