В данной статье представлены элементы введения в классификацию с обучением на небольших выборках — от удобной системы обозначений до специальных оценок надежности.
Постоянное увеличение быстродействия вычислительных устройств и малая выборка позволяют пренебречь значительным объемом вычислений, необходимых для получения некоторых из этих оценок.
Определения и обозначения
Пусть задано некоторое начальное разбиение множестваобъекты
на два подмножества (класса)
, такой, что
,
.
(1)
Мы отождествим двухклассовый классификатор с бинарной функцией вида
(2)
Где
— случайные выборки-подмножества
из занятий
,
- исследуемый объект, который необходимо отнести к одному из классов.
Значения этой функции будут интерпретироваться как «решения» по правилу
(3)
В зависимости от того, соответствуют ли решения классификатора исходному разделу.
на классы, будем считать их «правильными» или «неправильными» соответственно.
Давайте тоже договоримся
элементы образцов
назначать 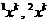
, так что соответственно:
,
(4)
Где
— объемы обучающих выборок.
Мы предполагаем набор
"погруженный в
-мерное правое евклидово пространство
.
Тогда все элементы класса
, включая, естественно, элементы обучающей выборки и исследуемого объекта, можно рассматривать как его точки.
Координаты точечных объектов из набора
мы отметим это правым нижним индексом
.
Координаты объекта
обучающие образцы будут записаны как
, объект исследования
Как -
.
В зависимости от контекста,
понимается либо как имя объекта, либо как радиус-вектор.
Исходим из отсутствия тестовой последовательности и оценок вероятности ошибки классификации.
будет проводиться в режиме скользящего экзамена
,
(5)
Где
,
(6)
.
(7)
Объекты
обучающие выборки, классифицированные в режиме скользящего обследования, в дальнейшем будем называть квазипроверенными.
Скорректированный скользящий экзамен
Известно, что скользящий экзамен имеет ряд недостатков.Эти недостатки можно в некоторой степени устранить путем корректировки скользящего экзамена.
Скорректированные оценки, отмеченные левой чертой, будут записаны следующим образом:
,
(8)
,
(9)
.
(10) К недостаткам скорректированного прокатного исследования следует отнести увеличенное количество операций и то, что эта оценка проводится на обеих пробах объемом на одну единицу меньше.
Таким образом, при небольших выборках оценка вероятности ошибки оказывается несколько завышенной, но по мере увеличения размера выборки этот эффект теряет свою значимость.
Соклассификатор
В связи с высокой сложностью скорректированного скользящего экзамена представляет интерес метод бинарной оценки достоверности классификации - коклассификатор.Как и скользящий экзамен, он может основываться исключительно на информации из обучающих выборок, но также может использоваться при наличии тестовых последовательностей.
Давайте представим образцы
объекты, соответственно правильно и ошибочно классифицированные классификатором (2) в режиме скользящего экзамена
,
(11)
.
(12)
Тогда решение коклассификатора первого порядка классификатора (2), определяемого как
,
(13)
интерпретируется следующим образом
Если
тогда классификатор (2) принял правильное решение относительно
,
Если
, то классификатор(2) принял ошибочное решение относительно
.
(14)
В этом случае будем считать, что образцы
извлеченные из определенных классов
объекты потенциально правильно или неправильно классифицированные классификатором (2).
При определении (13) предполагается, что размер выборки
не слишком маленький.
Таким образом, если у нас есть только материал обучающей выборки и нет тестовых последовательностей, то рекомендуется использовать соклассификатор в условиях, когда классификатор (2) допускает значительное количество ошибок.
Если вы все еще используете соклассификатор в небольшой выборке
, то его следует выбирать в достаточно простой форме.
Например, если коклассификатор типа Фишера, можно предположить, что ковариационная матрица диагональна или даже равна единице.
Подобно адаптивному повышению, композиция классификатора
можно рассматривать как коллективный классификатор, организованный существенно более нелинейно по сравнению с предложенными в [1].
Остановимся на вопросах, связанных с выбором конкретной формы соклассификатора.
Пусть, например, образцы
извлечено из классов
с плотностями распределения
, и классы сильно перекрываются.
В этом случае часто может оказаться, что плотности выборки
имеют схожие средние значения.
В этом случае соклассификатор
может быть выбран, например, в виде линейного классификатора Фишера, модифицированного с помощью процедуры Петерсона-Маттсона [2,3].
Фрактальный классификатор
Процесс синтеза коклассификаторов более высоких порядков может быть продолжен в рамках рекуррентной процедуры, когда первоначально осуществляется замена, (15) то, повторяя описанный выше алгоритм, получим на выходе коклассификатор второго порядка
.
(16) и продолжите эту процедуру.
Императивная остановка происходит при построении соклассификатора этого порядка.
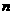
, при котором
или даже
.
В результате мы получаем итерированную систему классификаторов – фрактальный классификатор.
Этот коллективный классификатор, конечно, не следует смешивать с классификаторами изображений, использующими для своей обработки фрактальные и вейвлет-преобразования.
На практике нам приходилось использовать только соклассификаторы первого порядка.
Они были разработаны нами много лет назад и зарекомендовали себя как полезные инструменты при решении различных практических задач, в частности, при анализе отраженных радиосигналов для систем обнаружения пластиковых противопехотных мин [4], а также в создание системы ЛЕКТОН.
Эта система позволяла полностью автоматически проверять подлинность подписей на чеках, векселях и других документах и была первой системой такого типа, фактически использованной в банке.
Вероятность локальной ошибки
В практических занятиях местные— оценки вероятности ошибки классификации.
Представим классификатор (2) в виде
,
(17)
Где
— оценки плотности
по образцам
соответственно.
Тогда местный
— оценку вероятности ошибки этого классификатора можно определить как
,
(18)
Где
.
Давайте представим специальный 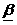
- оценка, которую можно рассматривать как «нечеткий» классификатор
(19)
Где
.
Тогда мы будем считать, что
интерпретируется как решение нечеткого классификатора, которое
,
- как решение, которое
.
Более того, чем ближе
к нулю или единице, тем более достоверны соответствующие решения нечеткого классификатора.
На основании оценки (19) определение классификатора (2) можно обобщить, введя зону или зоны отказа.
Соответствующее обозначение ширины этих зон
, представим их в следующем виде
(20)
Где
— границы зон.
Если асимметрии в требованиях к зонам нет, выберите
.
Литература: 1. Архипов Г.
Ф.
Коллективы определяющих правил: оптимальные решения и некоторые характеристики надежности классификации.
– В сборнике статей «Статистические проблемы управления», Вильнюс, 1983, т.61, стр.
130-145. 2. Мясников В.
В.
О модификациях метода построения линейной дискриминантной функции на основе процедуры Петерсона-Маттсона.
компьютероптика.
smr.ru/KO/PDF/KO26/KO26211.pdf. 3. Фукунага К.
Введение в статистическую теорию распознавания образов.
М.
«Наука» 1979. С.
105-130. 4. Архипов Г.
, Клышко Г.
, Стасайтис Д.
, Левитас Б.
, Аленкович Х.
, Ефремов С.
Исследование металлических и диэлектрических подземных объектов на основе оригинальной компьютерной методики распознавания отраженных радиосигналов.
МИКОН-2000., XII Международная конференция по микроволновому излучению, радиолокации и беспроводной связи, Том 2, стр.
495-498./> Теги: #распознавание образов #ошибки #классификатор #фрактал #Интеллектуальный анализ данных #Алгоритмы #Машинное обучение
-
Пасхалки Олимпиады 2010 От Яндекса
19 Oct, 24 -
Гарри Поттер И Методы Рационального Мышления
19 Oct, 24 -
Хонда Фкх
19 Oct, 24


