Минимизация логических функций — одна из типичных задач в процессе обучения схемотехнике.
Поэтому думаю, что такая статья имеет место, надеюсь, она вам понравится.

Почему это необходимо?
Сложность логической функции, а значит, сложность и стоимость реализующей ее схемы (схемы) пропорциональны количеству логических операций и числу вхождений переменных или их отрицаний.В принципе, любую логическую функцию можно упростить непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких вычислений.
Кроме того, процесс упрощения логических выражений не является алгоритмическим.
Поэтому целесообразнее использовать специальные алгоритмические методы минимизации, позволяющие упростить функцию более просто, быстро и безошибочно.
К таким методам относятся, например, метод Куайна, метод карты Карно, метод импликантного теста, метод импликантной матрицы, метод Куайна-МакКласки и другие.
Эти методы наиболее подходят для рутинной практики, особенно для минимизации логической функции с помощью карт Карно.
Метод карты Карно сохраняет наглядность при числе переменных не более шести.
В случаях, когда количество аргументов больше шести, обычно используется метод Куайна-МакКласки.
В процессе минимизации той или иной логической функции обычно учитывают, на каком основании было бы эффективнее реализовать ее минимальную форму с помощью электронных схем.
Минимизация логических функций с использованием карт Карно
Карта Карно — это графический способ минимизации коммутационных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и исключающий потенциальные гонки.Представляет собой операции попарного неполного склеивания и элементарного поглощения.
Карты Карно рассматриваются как таблица истинности функции, перестроенной соответствующим образом.
Карты Карно можно рассматривать как специфическую плоскую разработку n-мерного булева куба.
Карты Карно были изобретены в 1952 году Эдвардом В.
Вейчем и улучшены в 1953 году Морисом Карно, физиком из Bell Labs, и предназначались для упрощения цифровых электронных схем.
В карте Карно булевы переменные переносятся из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего всего на одну цифру.
Основным методом минимизации логических функций, представленных в виде SDNF или SCNF, является операция попарной неполной склейки и элементарного поглощения.
Операция попарной склейки осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и обратные) совпадают для всех переменных, кроме одной.
В этом случае все переменные, кроме одной, можно вынести за скобки, а прямые и обратные вхождения одной переменной, оставшейся в скобках, склеить.
Например: 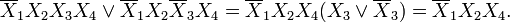
Возможность поглощения следует из очевидных равенств 
Таким образом, основной задачей минимизации SDNF и SCNF является поиск термов, пригодных для склеивания с последующим поглощением, что может оказаться весьма сложной задачей для больших форм.
Карты Карно предоставляют визуальный способ найти такие термины.
Как известно, булевы функции от N переменных, представленные в виде SDNF или SCNF, могут содержать 2N различных термов.
Все эти термы составляют некую структуру, топологически эквивалентную N-мерному кубу, причем любые два терма, соединенные ребром, пригодны для склейки и поглощения.
На рисунке изображена простая таблица истинности для функции двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением термов SDNF и эквивалентная таблица группировки термов: 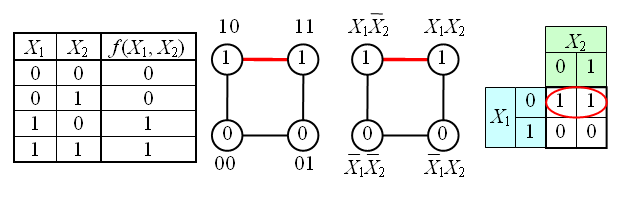
В случае функции трех переменных приходится иметь дело с трехмерным кубом.
Это сложнее и менее наглядно, но технически возможно.
На рисунке в качестве примера показана таблица истинности для булевой функции трех переменных и соответствующий ей куб.
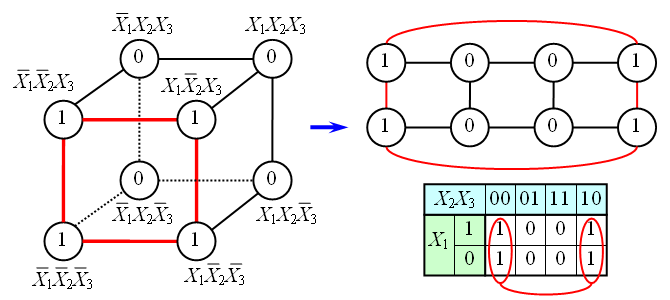
Как видно из рисунка, для трехмерного случая возможны более сложные конфигурации термов.
Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных: 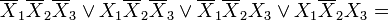
В общем, можно сказать, что 2K термов, принадлежащих одной K-мерной грани гиперкуба, склеены в один терм, а K переменных поглощены.
Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный прием.
Куб, представляющий структуру термов, развернут на плоскость, как показано на рисунке.
Это позволяет представлять логические функции с более чем двумя переменными в виде плоской таблицы.
Следует помнить, что порядок кодов терминов в таблице (00 01 11 10) не соответствует порядку двоичных чисел, а ячейки, расположенные во внешних столбцах таблицы, соседствуют друг с другом.

Аналогичным образом можно работать с функциями четырех, пяти и более переменных.
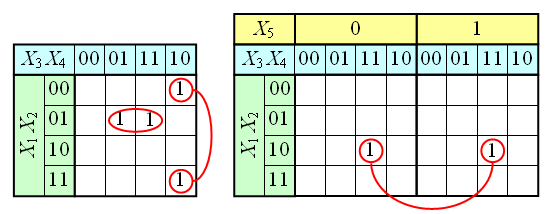
Примеры таблиц для N=4 и N=5 показаны на рисунке.
Для этих таблиц следует помнить, что соседними ячейками являются те, которые расположены в соответствующих ячейках внешних столбцов и соответствующих ячейках верхней и нижней строки.
Для таблиц с 5 и более переменными необходимо также учитывать, что квадраты 4х4 виртуально располагаются друг над другом в третьем измерении, поэтому соответствующие ячейки двух соседних квадратов 4х4 являются соседними, и соответствующие им термы могут быть склеены.
Карту Карно можно составить для любого числа переменных, но удобно работать не более чем с пятью переменными.
По сути, карта Карно — это таблица истинности, составленная в двухмерной форме.
Благодаря использованию кода Грея верхняя строка соседствует с нижней, а правый столбец соседствует с левой, т.е.
вся Карта Карно сворачивается в фигуру тора (бублика).
На пересечении строки и столбца вставляется соответствующее значение из таблицы истинности.
После того, как Карта заполнена, можно приступать к минимизации.
Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те ячейки, которые содержат единицы; если нужна КНФ, то рассматриваем те ячейки, которые содержат нули.
Сама минимизация осуществляется по следующим правилам (на примере ДНФ):
- Объединим соседние ячейки, содержащие единицы, в регион так, чтобы в одном регионе было 2 н ( н целое число = 0.
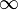
) ячейки (помните, что крайние строки и столбцы соседствуют друг с другом), в области не должно быть ячеек, содержащих нули; - Область должна располагаться симметрично оси(ям) (оси расположены через каждые четыре ячейки);
- Несмежные области, расположенные симметрично оси(ям), могут быть объединены в одну;
- Площадь должна быть как можно больше, а количество площадей как можно меньше;
- Области могут пересекаться;
- Возможны несколько вариантов покрытия.
Возьмите следующую область, проделайте то же самое, что и с первой, и так для всех областей.
Соединяем соединения областей путем дизъюнкции.
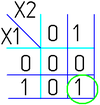
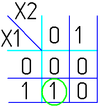
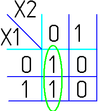
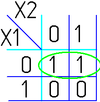
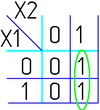
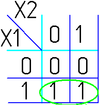
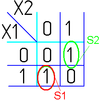
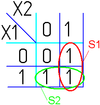
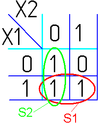
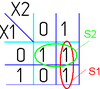
Например (для карт с двумя переменными):
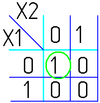 |
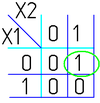 |
 |
 |
 |
 |
 |
 |
|||||||
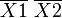 |
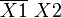 |
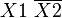 |
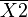 |
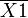 |
||||||||||
 |
 |
 |
 |
 |
 |
|||||||||
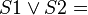 |
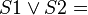 |
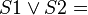 |
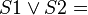 |
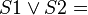 |
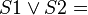 |
|||||||||
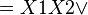 |
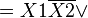 |
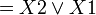 |
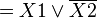 |
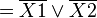 |
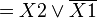 |
|||||||||
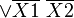 |
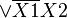 |
На этом минимизация считается завершенной.
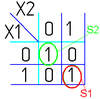
Так для Карты Карно на рис.
1 выражение в формате DNF будет выглядеть так: 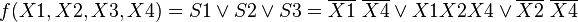
В формате CNF: 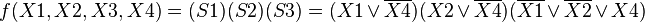
Теги: #Электроника для начинающих #схемотехника #минимизация логических функций

-
Security Essentials Не Так Уж И Плох
19 Oct, 24 -
Отчет Меньшинства
19 Oct, 24


