Однажды, на втором курсе университета, мне дали задание состряпать что-то «вроде этого», чтобы подтвердить высокое звание «будущего инженера-робототехника».
На этой пафосной ноте я отправился в глубины разума в поисках идей.
После небольшой поездки появилась идея устройства, теорией которого я хочу поделиться с общественностью.
Суть разработки такова.
Рассмотрим обычный, скажем, 5-осевой манипулятор (кинематическая структурная схема представлена на рисунке ниже).
Его возможности при перемещении в пространстве широки: он способен совершать движения по 5 координатам, причем одновременно, т.е.
по 3 координатам по трем осям XYZ и вращению вокруг двух из них.
При этом рабочий элемент манипулятора способен занимать любое положение в рабочем пространстве и при этом сохранять необходимую ориентацию рабочего элемента (не считая вращения рабочего элемента вокруг собственной оси).
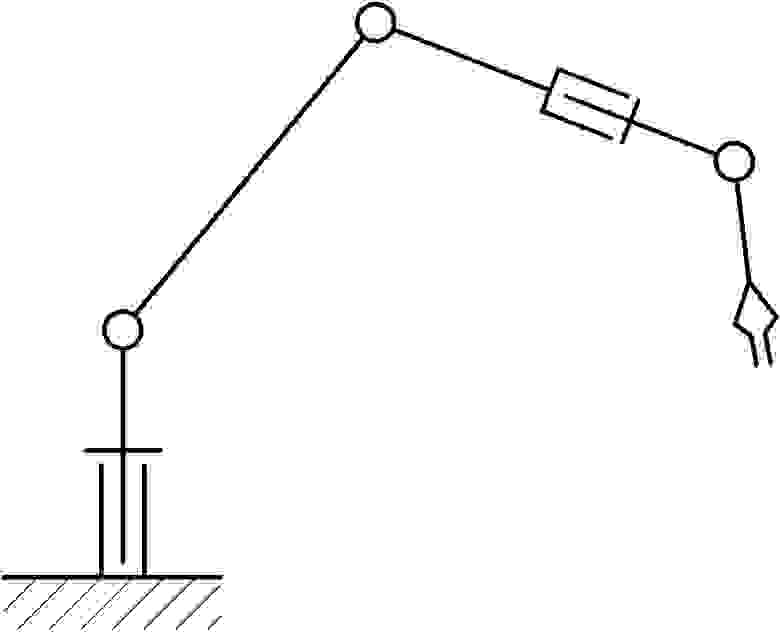
Данная конструкция относится к антропоморфному типу манипуляторов и поэтому способна приближенно воспроизводить движение руки человека.
Пока размышлял над этим тезисом, мне как раз пришла мысль, что было бы интересно сделать так, чтобы манипулятор мог удаленно копировать движения моей руки в реальном времени.
Чтобы я просто надел на руку датчик, который считывает движения моей руки (как линейные, так и угловые), а эта механическая штука будет повторять их за мной.
Как манипулятор может выполнять функции перемещения и ориентации рабочего органа, так и человек с помощью руки может перемещать и ориентировать свою ладонь, поэтому эти два процесса схожи и их можно представить как один общий процесс – захват движение руки манипулятором в реальном времени.
Выкатил губу Забегая вперед, скажу, что уловить удалось только ориентирующее движение ладони, т.е.
я мог контролировать ориентацию рабочего органа, но не его линейное движение в пространстве.
На этом постановка задачи завершена.
Теперь разберем задачу (техническим заданием ее назвать сложно).
Необходимо разработать два конструктивно независимых устройства: сам манипулятор и устройство отслеживания движения, которое крепится к руке.
Далее последует трудоемкий процесс создания математических описаний, составления алгоритма и написания программного обеспечения.
Мы разделяем проект на три части: 1. Разработка манипулятора 2. Разработка устройства отслеживания движения рук.
3. Все остальное Коротко о каждом из этапов:
- Здесь все тривиально.
Мы проектируем конструкцию в САПР, делаем чертежи деталей и изготавливаем их, затем собираем.
Дальше рассчитываем кинематику и пишем свое ПО, которое будет скрывать низкоуровневые обращения к приводам.
- На этом этапе мы определяемся с типом датчиков, проектируем принципиальную схему, изготавливаем печатную плату, разрабатываем алгоритм определения положения в пространстве и пишем программное обеспечение.
- Собственно, для чего были предыдущие этапы – заставить манипулятора подчиняться хозяину.
Здесь я разрабатываю алгоритм преобразования координат в рабочее поле манипулятора.
1. Разработка манипулятора
В этом проекте, как уже говорилось выше, мы используем манипулятор с 5 степенями свободы.Этого количества степеней свободы достаточно, поскольку они включают в себя три линейных движения и два вращательных.
Последние два необходимы для ориентации рабочего органа, так как направление РО в пространстве можно задать в виде вектора, а вектор однозначно можно восстановить по двум углам поворота (не учитывая длину).
.
В данном случае нам понадобятся пять обобщенных координат, равных числу осей.
Звенья манипулятора соединены вращательными кинематическими парами пятого класса.
Конструкция манипулятора стандартна для своего типа (кинематическая схема представлена в начале статьи).
Он состоит из неподвижной рамы, с которой связана базовая система координат, поворотной стойки, к которой прикреплены остальные подвижные звенья, соединенные в цепь.
Рабочий элемент крепится к торцевому звену (фланцу), в данном случае его имитации в виде стреловидного индикатора (см.
изображение ниже).
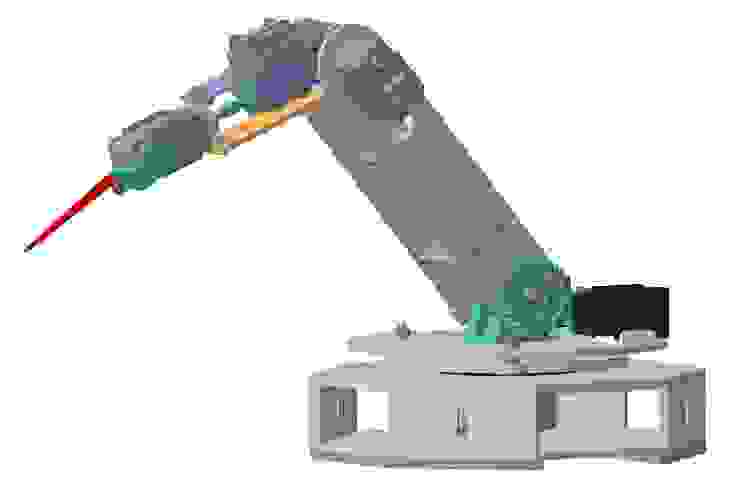
Фотоотчет о сборе














3D-модель построена в САПР «Компас 3D».
Материал деталей — фанера толщиной 4 мм и PLA для пластиковых деталей.
Детали из фанеры вырезались на лазерном станке, пластиковые детали распечатывались на 3D-принтере.
В качестве привода осей используются цифровые сервоприводы Dynamixel AX-12. Внешний вид манипулятора напоминает некое мерзкое насекомое, от которого он и получил прозвище «Комар».
Математическое описание кинематики
На этом этапе необходимо рассчитать прямую и обратную кинематику манипулятора.Непосредственной задачей является определение положений звеньев относительно некоторой базовой системы координат по известным значениям обобщенных координат (в данном случае углов поворота звеньев).
Ее обратная задача называется обратной или обратной кинематикой и заключается в определении параметров обобщенных координат для достижения желаемого положения и ориентации рабочего органа манипулятора.
Начнем с расчета обратной кинематики.
Изобразим геометрическую схему манипулятора, из которой будут понятны интересующие нас геометрические соотношения.
Требуемую позицию представляем радиус-вектором
.
Здесь стоит объяснить, почему вектор
проводится до точки фланца, а не до конечной точки РО.
Поскольку ориентация рабочего органа нам заранее известна (определяю ее сам по некоторым требованиям), необходимо, чтобы точка фланца находилась в нужном месте, обозначенном как вектор
.
Этот вектор получается вычитанием из радиус-вектора
, проведенный к конечной точке РО, вектор его ориентации
, относительно BSC, т.е.
:
Учитывайте переход точки фланца в нужное положение.
Осуществляется поворотом звеньев а И б (я изобразила их векторами) в петлях А , Б И С .
Начало базовой системы координат (БСК) размещается в шарнирной точке.
Б .
Ось вращения шарнира А направлен вдоль оси З , топоры Б И С направлен перпендикулярно З .
Когда все формальности выполнены, приступаем к делу.
Для решения обратной задачи кинематики я использовал геометрический подход ввиду простоты конструкции манипулятора.
Из геометрии ясно, что вектор
равен сумме векторов связей
И
.
Углы
,
,
- углы поворота звеньев А , В И С соответственно.
Рассмотрим треугольник, ограниченный векторами
,
И
.
Из этого треугольника, используя теорему косинусов, находим углы
И
.
Пусть длины векторов равны:
Запишем теорему косинусов относительно искомых углов:
Давайте выразим углы
И
:
Из геометрической диаграммы видно, что:
Затем:
Наконец, переход от линейных координат к углам поворота звеньев осуществляется по формулам:
Теперь, когда вы переместили точку фланца в необходимое положение, вам необходимо правильно сориентировать рабочий элемент. Для этого нужно знать координаты вектора
относительно точки фланца, т.е.
координаты в основе местной системы координат (ЛСК) –
, начало которого находится в точке фланца манипулятора.
Вектор
отправил по ссылке б , вектор
– по оси шарнирного соединения ф1 .
Чтобы найти основу
определим матрицу перехода из БСК (с базисом
) и ЛСК.
Данная матрица получается комбинацией вращений на шарнирах А , Б И С :
Где
Потому что матрица
унитарна, то:
Знающему читателю
Знающий читатель может найти здесь сходство с представлением Денавита–Хартенберга для решения прямой задачи кинематики.
Да, вот оно, упрощенное до крайности и с моими небольшими изменениями.
Здесь я не использую однородные преобразования, не учитываю конструктивные особенности, такие как угловое и линейное смещение осей и т.п.
Я просто спроектировал конструкцию так, чтобы отсутствовали упомянутые выше лишние параметры, оставив только обобщенные координаты.
Матрица
рассчитывается путем умножения поворот матрицы вокруг оси на угол .
Давайте определим функцию, которая вычисляет эту матрицу:
Ось берется в качестве вектора как столбец матрицы, полученной предыдущими вращениями, а углы уже рассчитаны выше.
В результате мы получаем:
Пусть вектор рабочего тела в БСК
.
Тогда равенство верно:
Отсюда мы выражаем
– вектор рабочего тела в базисе
, т.е.
относительно точки фланца:
Теперь, зная вектор РО, мы можем рассчитать углы поворота ориентирующих осей ф1 И f2 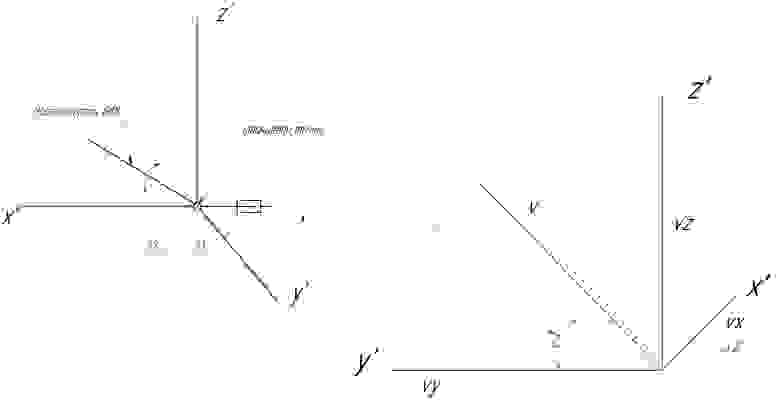
Чтобы переместить РО в заданное положение, нужно вращать на углы
И
.
Из рисунка ясно, что
Где
— длина рабочего органа,
— векторные координаты
.
Программное обеспечение манипулятора разделено на два уровня: верхний и нижний.
Верхний уровень написан в Matlab в виде библиотеки и с использованием различных команд и методов, нижний уровень написан на микроконтроллере Atmega328. Задача верхнего уровня — формулировать команды, отправляемые микроконтроллеру.
Его задача – получить команду и в соответствии с ней установить приводы в нужное положение.
В таком виде система управления оказалась надежной (пока.
) и простой в использовании.
Почему Матлаб? Изюминка, как по мне, языка Matlab в том, что операции с матрицами происходят там как обычные алгебраические отношения, и нет необходимости создавать вложенные циклы, как это сделано, например, в языке C. Плюс в Матлабе доступна практически любая «нужная» математическая операция, что приносит огромное счастье.
Команда формулируется и отправляется с верхнего уровня следующим образом: пользователь вызывает в окне команд Matlab функцию из библиотеки (например, функцию простого перемещения в точку), задает необходимые аргументы (обычно координаты и ориентацию).
РО).
После этого на основе приведенных выше математических соображений, записанных в библиотеке, рассчитываются углы поворота осей и, при необходимости, скорость вращения.
Далее по простому протоколу собираем команду и отправляем ее на микроконтроллер нижнего уровня через последовательный COM-порт. Несколько слов о письменной библиотеке.
В его распоряжении имеются следующие функции:
- функции для создания соединения через последовательный интерфейс
- функции движения
- до точки, при постоянной скорости всех приводов
- до точки, с окончательной остановкой всех приводов (скорость привода выбирается пропорционально собственному и наибольшему углу поворота.
Таким образом, в конце подхода к точке все приводы прекращают движение)
- до точки, с плавным движением каждого привода (график скорости в этом случае имеет вид трапеции с участками разгона, постоянной скорости и торможения) Расписание
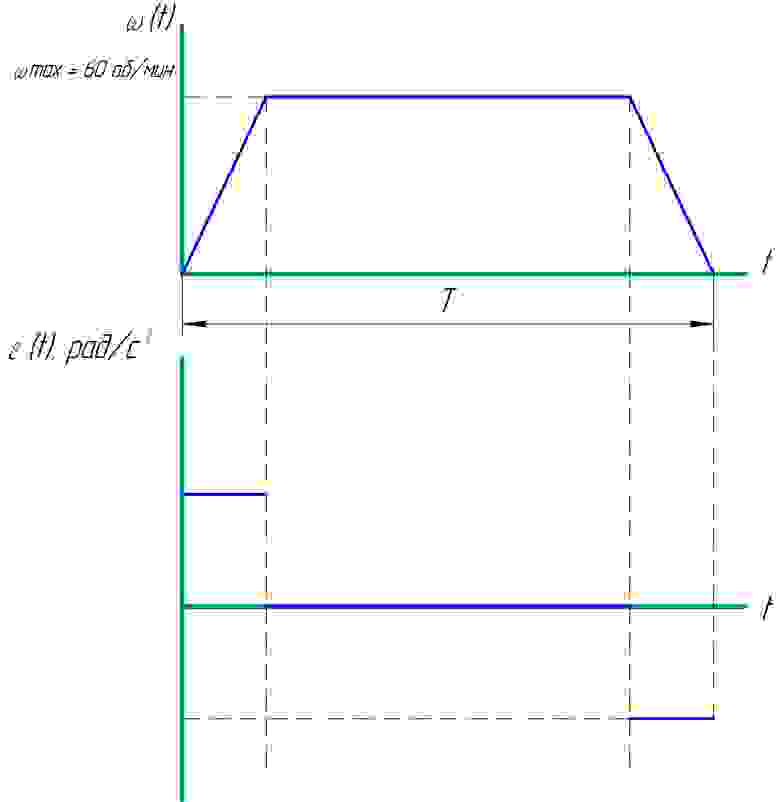
- в точку, согласно заданным вручную углам поворота осей и скорости вращения
Видео демонстрирует работу манипулятора.
2. Разработка устройства отслеживания движения рук.
Перейдем к следующему этапу.
Здесь вам потребуется сконструировать специальное устройство, способное отслеживать положение ладони в пространстве в режиме реального времени.
Этот процесс еще называют «захват движения».
Для реализации своего замысла я решил использовать бесплатформенную инерциальную навигационную систему (БИНС) на основе трех датчиков: гироскопа, ускорителя и магнитометра.
Комбинация этих датчиков называется ИМУ – сенсор (в переводе это и есть БИНС).
Сначала я спроектировал печатную плату с нужным мне функционалом, на которой разместил эти три датчика.
В качестве контроллера обработки я выбрал (вернее взял то, что было в наличии) микроконтроллер Atmega2560. Я использовал датчики, которые распространены и дешевы на китайском рынке.
Это парные трехосные датчики: гироскоп и акселерометр MPU6050 и магнитометр HMC5883l. 
Фото готовой платы
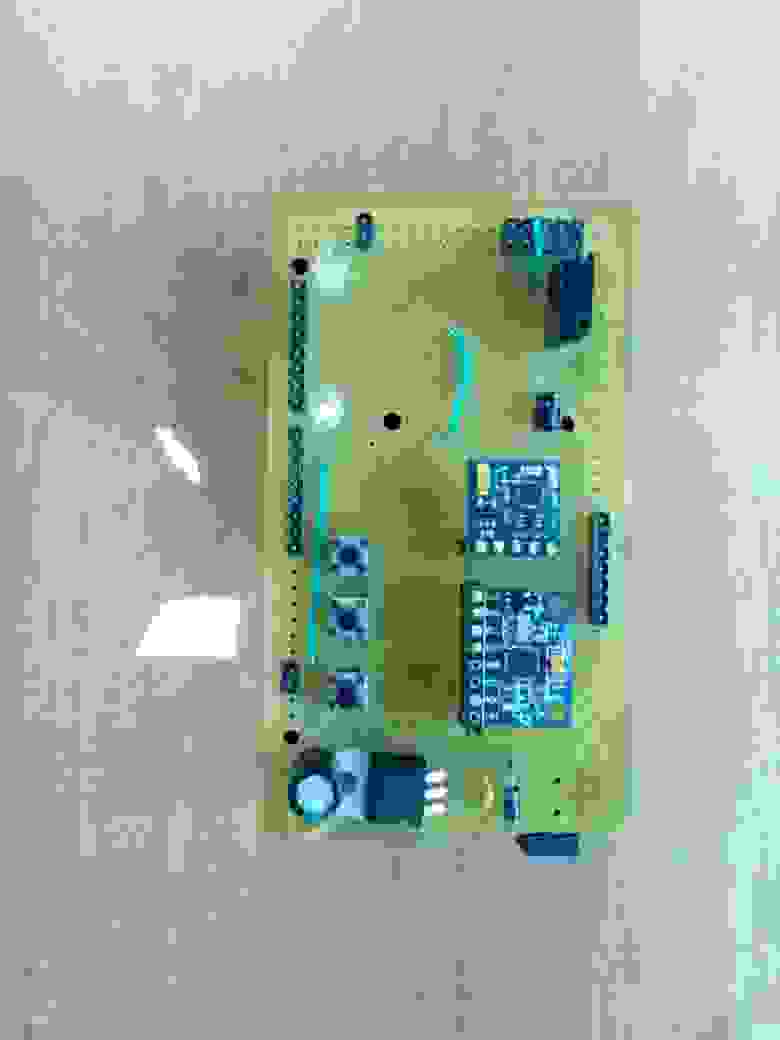

Алгоритм расчета положения в пространстве довольно прост: сначала мы определяем ориентацию в виде основы местной системы координат (ЛСК), которая связана с датчиками, и в конечном итоге с ладонью.
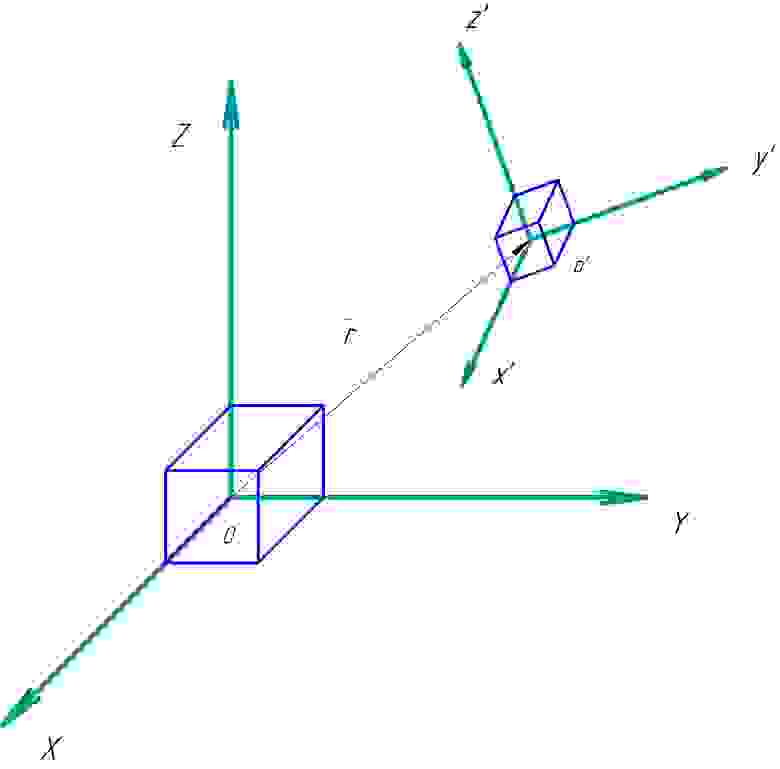
Ориентация определяется относительно исходной системы координат (ИСК), которая по сути является исходным положением устройства в момент включения питания.
Базы NSK и LSK состоят из векторов-столбцов его единичного вектора:
Они связаны соотношением:
Где
– матрица перехода, также известная как матрица вращения в пространстве.
Основой НСК будем считать единичную матрицу.
Следовательно
.
После этого вектор ускорения
, который известен относительно ЛСК, должен быть определен в НСК.
Это делается путем умножения вектор-столбца ускорения на базис LCS:
Затем дважды интегрируем полученный вектор ускорения по времени и получаем расстояние, т.е.
координаты:
Первые попытки реализовать этот алгоритм были очень наивными.
Наивность заключалась в том, что я считал возможным только по данным гироскопа, используя дискретное интегрирование, получить матрицу вращения вокруг оси.
Ось в этом случае можно рассматривать как псевдовектор угловой скорости, компоненты которого (проекции на ось) являются выходными данными датчика гироскопа.
А угол, в свою очередь, получается интегрированием модуля вектора.
Первоначальное волнение и энтузиазм исчезли, когда я увидел чудовищную величину так называемого «дрейфа нуля», вызванного накапливающейся ошибкой из-за ошибки дискретного интегрирования и собственного шума датчика.
Уже тогда у меня возникли мысли, что по данным акселерометра, который в состоянии покоя показывает вектор, обратный вектору ускорения свободного падения (далее по тексту вектор силы тяжести), можно внести корректировку в матрицу , но и тут есть неопределённость, связанная с тем, что регулировка возможна только с точностью до поворота угла вокруг оси Z. Коррекция будет полной, если удастся восстановить матрицу вращения альтернативным способом, т.е.
без использования данных гироскопа.
Для особо заинтересованных Поясню для особо интересующихся.
Почему невозможно восстановить матрицу вращения с помощью акселерометра? Точнее, данных недостаточно.
Как мы знаем, вектор гравитации всегда направлен к центру планеты, а значит, перпендикулярен поверхности Земли.
Потому что мы сопоставляем исходную систему координат, например, со столом так, чтобы плоскость XY была параллельна поверхности стола, которая в свою очередь параллельна (с некоторой условностью) полу, а пол в свою очередь параллелен к плоскости основания здания, которая обычно представляет собой касательную плоскость к поверхности Земли.
Отсюда делаем вывод, что показания акселерометра в состоянии покоя (или при равномерном движении) говорят нам о положении оси
LSC по отношению к NSC. На этом полезность этих данных заканчивается, ведь вращение вокруг оси
не изменит саму ось
, но меняет две другие оси
И
.
Следовательно, показания акселерометра не изменятся и тогда положение определяться не будет. Тогда необходимо использовать еще один фактор, согласно которому можно будет произвести полную корректировку положения.
Этим фактором является магнитное поле Земли, которое вместе с гравитацией в любой данной точке планеты не меняется с течением времени (в краткосрочной перспективе, конечно).
Мы измеряем его с помощью вышеупомянутого датчика HMC5883l. В данном случае у нас есть два вектора, которых достаточно для определения n по ним Теги: #Сделай сам или Сделай сам #Разработка робототехники #Робототехника #манипулятор #кватернион #imu

-
Новый Дизайн Хабра? :)
19 Oct, 24 -
Я Веб-Разработчик, Дизайнер И Т. Д.
19 Oct, 24


