Стандартная гауссова статистика работает на основе следующих предположений.
Центральная предельная теорема утверждает, что по мере увеличения числа испытаний предельное распределение случайной системы становится нормальным.
События должны быть независимыми и одинаково распределенными (то есть они не должны влиять друг на друга и иметь одинаковую вероятность возникновения).
При изучении больших сложных систем принято предполагать, что система нормальна, поэтому можно применить стандартный статистический анализ.
Часто на практике изучаемые системы (от солнечных пятен, среднегодовых осадков до финансовых рынков, временных рядов экономических показателей) не имеют нормального распределения или близки к нему.
Для анализа таких систем Херст [1] предложил метод Нормализованный диапазон (RS-анализ).
В основном этот метод позволяет различать случайные и фрактальные временные ряды, а также делать выводы о наличии непериодических циклов, долговременной памяти и т. д.
Алгоритм анализа RS
- Судя по оригинальному сериалу

.Посчитаем логарифмические отношения:
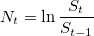
- Давайте разделим серию

на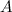
смежные периоды длины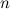
.Обозначим каждый период как
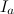
, Где
.Определим для каждого
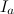
Средняя стоимость:
- Рассчитаем отклонения от среднего значения для каждого периода
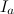
: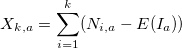
- Рассчитаем диапазон внутри каждого периода:
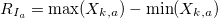
- Рассчитаем стандартное отклонение для каждого периода
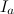
:
- Каждый

Поделить на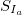
.Далее вычисляем среднее значение Р/С :

- Мы увеличиваем
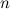
и повторяйте шаги 2–6, пока
- Построение графа зависимостей

от
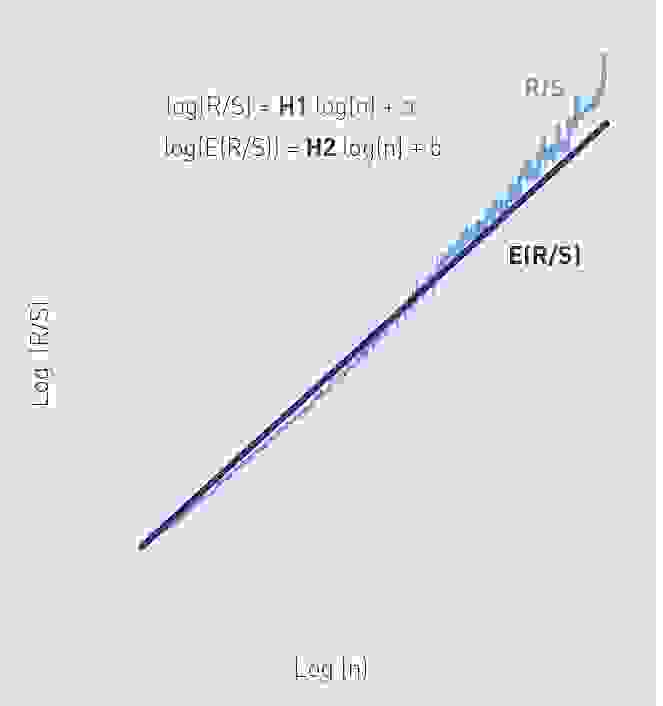
и используя метод наименьших квадратов, мы находим регрессию вида:
, Где ЧАС – показатель Херста (см.рисунок).
Проверка значимости
Далее проверяем полученный результат на значимость.Для этого проверяем гипотезу о нормальном распределении анализируемой структуры.
Р/С являются случайными величинами, нормально распределенными, то можно считать, что ЧАС также нормально распределены.
Асимптотическим пределом независимого процесса является показатель Херста, равный 0,5. Нис и Ллойд [2], а также Питерс [3] предложили использовать следующие ожидаемые показатели: Р/С : 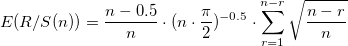
Для н наблюдений мы находим ожидаемый показатель Херста: 
.
Ожидаемое отклонение составит: 
, Где Т — количество наблюдений в выборке.
Пример статистики: 
.
Сравниваем его с критическим значением нормированного нормального распределения.
Если значение выборки меньше критичен, то гипотеза о нормальном распределении системы мы не отвергаем на этом уровне значимости.
Структура случайна и имеет нормальный закон распределения.
Библиография:
- Херст, Г.
?.
, 1951. «Долгосрочная емкость резервуаров».
Труды Американского общества инженеров-строителей, 116, 770-808.
- Анис А.
А.
, Ллойд ?.
Х.
(1976) Ожидаемое значение скорректированного масштабированного диапазона Херста независимых нормальных слагаемых.
Биометрика 63: 283-298.
- Питерс, ?.
?.
(1994) Фрактальный анализ рынка.
Уайли, Нью-Йорк.
ISBN 0-471-58524-6.

-
Mars Express Будет Работать До 2018 Года.
19 Oct, 24 -
Coco Framework — Блокчейн В Широком Смысле
19 Oct, 24


