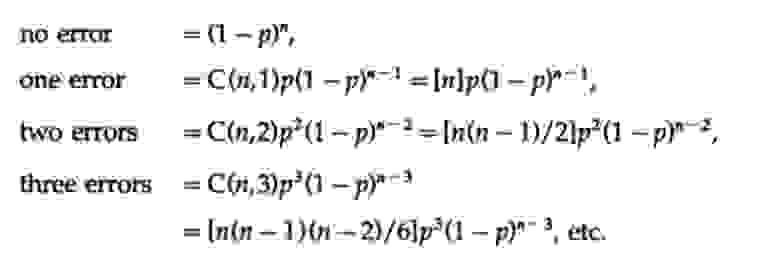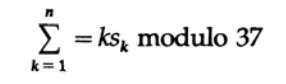«Цель этого курса — подготовить вас к вашему техническому будущему».Теги: #Ричард Хэмминг #Форсайт #Учимся учиться #будущее #цифровая экономика #Системная инженерия #Алгоритмы #математика #Профессиональная литература #Исследования и прогнозы в ИТ #Читальный зал
Привет, Хабр.Помните замечательную статью «Ты и твоя работа» (+219, 2442 закладки, 393 тыс.
прочтений)? Так что Хэмминг (да-да, самоконтроль и самокоррекция Коды Хэмминга ) есть целое книга , написанная по мотивам его лекций.
Мы переводим это, потому что мужчина высказывает то, что думает. Это книга не просто об ИТ, это книга о стиле мышления невероятно крутых людей.
«Это не просто стимул позитивного мышления; оно описывает условия, которые увеличивают шансы на выполнение великой работы».
Мы уже перевели 25 (из 30) глав.
И мы работаем над бумажным изданием.
11. Теория кодирования – II
(Спасибо за перевод еросинка , откликнувшийся на мой призыв в «предыдущей главе.») Кто хочет помочь с переводом — пишите в личку или на почту [email protected] Из предыдущей главы должны быть ясны две вещи.
Во-первых, мы хотим, чтобы средняя длина L отправленного сообщения была как можно меньше (для экономии ресурсов).
Во-вторых, это должно быть подкреплено статистической теорией, поскольку мы не можем знать, какое сообщение будет отправлено, но мы можем знать некоторую статистику, используя предыдущие сообщения, и последующие результаты, вероятно, будут аналогичны предыдущим.
Для простейшей теории, которую мы можем здесь обсудить, нам понадобятся вероятности появления отдельных символов в сообщении.
Их получение не является частью теории, но их можно получить, исследуя прошлый опыт или представляя будущее использование системы, которую вы проектируете.
Таким образом, нам нужен мгновенно однозначно декодируемый код для данного набора входных символов si и их вероятностей pi. Какую длину li нам следует установить (учитывая, что мы должны подчиняться неравенству Крафта), чтобы получить минимальную среднюю длину кода? Хаффман решил эту проблему проектирования кода.
Хаффман был первым, кто показал, что следующие неравенства должны быть верны для кода минимальной длины.
Если числа «пи» расположены в порядке убывания, то числа «li» должны быть в порядке возрастания.
Предположим, что pi находится в указанном порядке, но по крайней мере одна пара li — нет. Рассмотрим эффект перестановки символов, связанных с этими двумя, которые не находятся в указанном порядке.До перестановки вклад этих двух членов уравнения в среднюю длину кода L
и после перестановки
Все остальные члены суммы L остаются прежними.Разницу можно записать как
Одно из этих слагаемых предполагается отрицательным, поэтому после перестановки двух символов средняя длина кода L уменьшится.Таким образом, для минимальной длины кода мы должны иметь два неравенства.
Далее Хаффман обнаружил, что мгновенно расшифровываемый код имеет дерево решений, и каждый узел должен иметь два выхода, иначе это тщетная попытка, следовательно, существуют два самых длинных символа одинаковой длины.
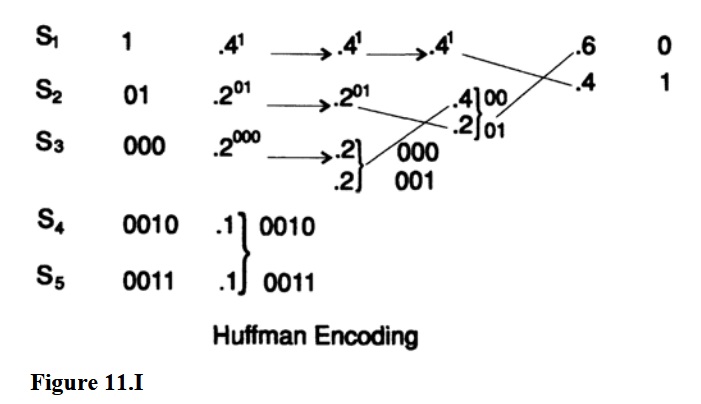
Для иллюстрации кода Хаффмана мы воспользуемся классическим примером.Пусть p(s1) = 0,4, p(s2) = 0,2, p(s3) = 0,2, p(s4) = 0,1 и p(s5) = 0,1. Это изображено на рисунке 11. Затем Хаффман утверждал, основываясь на приведенных выше значениях, что он может объединить (объединить) два наименее частых символа (которые должны быть одинаковой длины) в один символ с общей вероятностью с общими битами.
до последнего бита, который отбрасывается.
таким образом получая на один код символа меньше.
(?) Повторяя это снова и снова, он пришел к системе с двумя символами, которым он знал, как присвоить кодовое представление, а именно один символ был 0, а другой - 1.
Теперь, идя в обратном направлении, нам нужно на каждом этапе разделить символ, полученный из комбинации двух символов, сохраняя те же ведущие биты, но добавляя 0 к одному символу и 1 к другому.Используя этот метод, мы приходим к коду минимальной длины L, снова см.
рисунок 11. I. Потому что, если бы существовал другой код с меньшей длиной L', то, выполняя шаги вперед, изменяющие среднюю длину кода на заданное число, он в итоге получится два символа со средней длиной кода меньше 1, что невозможно.
Следовательно, код Хаффмана имеет минимальную длину.
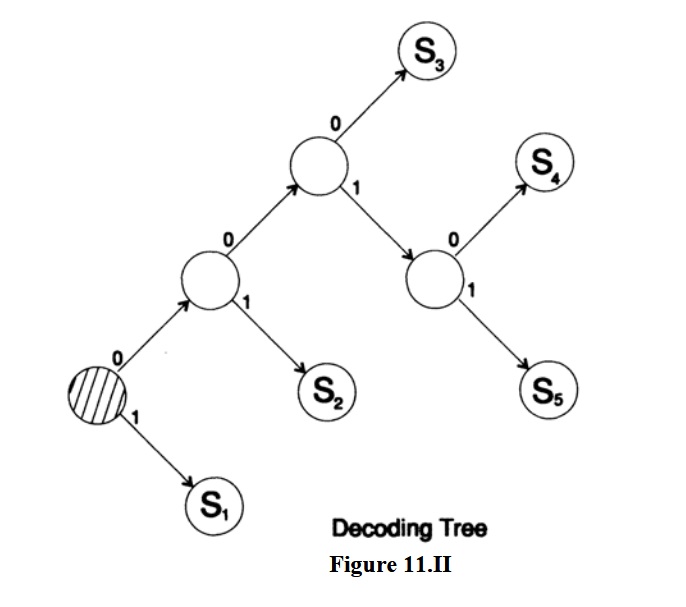
См.
рисунок 11.II для соответствующего дерева декодирования.
Этот код не уникален.
Прежде всего, на каждом этапе процесса присвоение 0 и 1 каждому из символов является произвольным процессом.
Во-вторых, если на каком-либо этапе встречаются два символа с равными вероятностями, то не имеет значения, какой из них будет первым.
В некоторых случаях это может привести к очень разным кодам, но они оба будут иметь одинаковую среднюю длину.
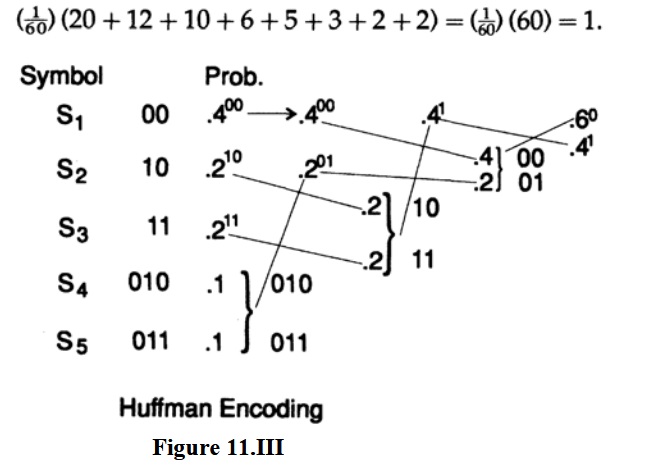
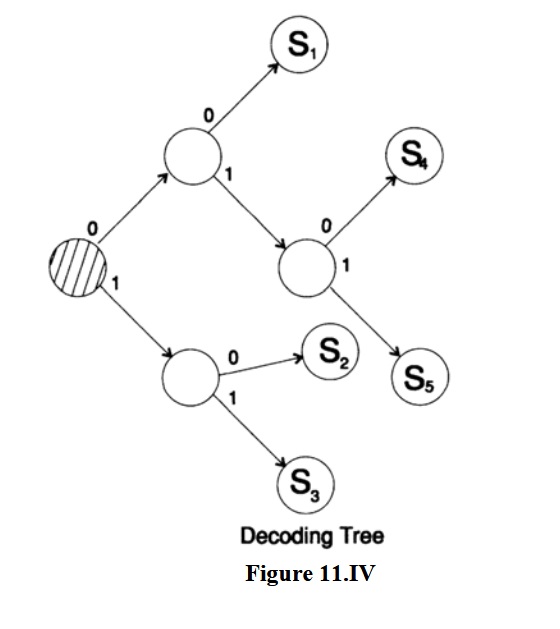
Если разместить объединенные термины как можно выше, то получим рисунок 11.III с соответствующим деревом декодирования на рисунке 11.IV. Средняя длина двух кодов одинакова, но коды и деревья декодирования различны; первый длинный, второй «ветвистый», а второй менее изменчив, чем первый.
Теперь мы приведем второй пример, чтобы дать вам уверенность в том, как работает кодирование Хаффмана, поскольку при разработке системы кодирования естественно хотеть использовать код с минимально возможной средней длиной.
Например, у вас может быть много данных, предназначенных для резервного хранения, и вы знаете, что кодирование их подходящим кодом Хаффмана позволит сэкономить более половины ожидаемой емкости хранилища.
Пусть p(s1) = ⅓, p(s2) = ⅕, p(s3) = ⅙, p(s4) = 1/10, p(s5) = 1/12, p(s6) 1/20, p( s7) = 1/30, p(s8) = 1/30. Сначала проверим, что сумма вероятностей равна 1. Общий знаменатель дробей равен 60. Это дает нам общую вероятность
Второй пример показан на рисунке 11.V, где мы опустили 60 в знаменателе вероятностей, поскольку имеют значение только относительные величины.Какова средняя длина кода на символ? Мы рассчитываем
Для блока кода из 8 символов каждый символ будет иметь длину 3, а средняя длина будет 3, что больше 2,58. Обратите внимание, насколько подходит этот механический процесс для машины.Каждый прямой шаг кодирования Хаффмана представляет собой повторение одного и того же процесса: объедините две наименьшие вероятности, поместите новую сумму в правильное место массива и отметьте ее.
В обратном процессе мы берем отмеченный символ и разделяем его.
Эти программы легко написать для компьютера, поэтому компьютерная программа может вычислить код Хаффмана на основе данных si и его вероятностей pi. Напомним, что на практике вам нужно назначить возвращаемый символ с очень маленькой вероятностью, чтобы можно было завершить процесс декодирования в конце сообщения.
Фактически, вы могли бы написать программу, которая могла бы отбирать данные для сохранения и находить оценку вероятности (небольшие ошибки приводят только к небольшим изменениям в L), находить код Хаффмана, выполнять кодирование и отправлять первый алгоритм декодирования (дерево) и затем закодированные данные, и все это без участия человека! В конце декодирования у вас уже есть дерево декодирования.
Таким образом, написав программу, вы сможете использовать ее в тех случаях, когда она окажется для вас полезной.
В некоторых компьютерах коды Хаффмана даже использовались в инструкциях, поскольку вероятность их использования была очень низкой.
Следовательно, нам нужно обратить внимание на улучшение средней длины кода L, которое мы можем ожидать при использовании кодирования Хаффмана по сравнению с простым блочным кодированием, которое использует одинаковую длину для всех символов.
Если все вероятности одинаковы и имеется ровно 2^k символов, то исследование кодирования Хаффмана покажет, что вы получите стандартный блочный код той же длины.
Если символов не ровно 2^k, то некоторые из них будут короче, но трудно сказать, будут ли большинство из них короче на 1 бит или некоторые будут короче на 2 и более бита.
В любом случае значение L будет таким же и не намного короче, чем в соответствующем блочном коде.
С другой стороны, если каждое из пи больше ⅔ (сумма всех последующих вероятностей, кроме последней), то вы получите код с точкой с запятой, в котором 1 символ имеет длину 1 (0), один символ имеет длину длина 2 (10) и так далее до конца, где у вас будет два символа одинаковой длины (q-1): (1111.10) и (1111.11).
В этом случае длина L может быть намного короче длины соответствующего блочного кода.
Правило: Кодирование Хаффмана окупается, когда вероятности символов сильно различаются, и не окупается, когда они примерно равны.
Когда в процессе Хаффмана появляются две равные вероятности, их можно расположить в любом порядке, и таким образом коды могут сильно различаться, хотя средняя длина кода L будет одинаковой в обоих случаях.
Естественно задаться вопросом, какой порядок следует выбрать в случае двух равных вероятностей.
Разумным критерием является минимизация вариаций кода, чтобы сообщения одинаковой длины в исходных символах имели примерно одинаковую длину в закодированной форме; вы не хотите, чтобы исходное короткое сообщение было случайно закодировано длинным сообщением.
Правило простое: каждую новую вероятность вставляйте в таблицу как можно выше.
Фактически, если вы разместите его над символом с несколько большей вероятностью, вы значительно уменьшите вариацию и лишь немного увеличите L; так что это хорошая стратегия.
Выполнив все шаги, перейдем к кодированию исходников (хотя мы далеко не всю тему рассмотрели).
Мы будем обращаться к каналу кодирования с моделируемым шумом.
Предполагается, что в канале присутствует шум, что означает, что некоторые биты были изменены во время передачи (или хранения).
Что может быть сделано? Найти единственную ошибку довольно просто.
К блоку из (n-1) бит вам нужно присоединить n-й бит со значением таким, чтобы все n бит имели четное количество единиц (или нечетное число, если хотите, но мы будем использовать четное число) .
Это называется проверкой четности (нечетности).
Таким образом, если все отправленные сообщения обладают этим свойством, то на принимающей стороне можно проверить, выполнено ли оно.
Если проверка четности не удалась, будет известно, что имеется по крайней мере одна ошибка, фактически нечетное количество ошибок.
Поскольку разумно использовать системы с низкой вероятностью ошибки в любом положении, вероятность множественных ошибок должна быть еще ниже.
Для математической приемлемости мы предполагаем, что канал представляет собой белый шум, что означает: 1) каждая позиция в блоке из n бит имеет ту же вероятность ошибки, что и любая другая позиция, и 2) ошибки в разных позициях некоррелированы, то есть независимы.
При этих предположениях вероятности ошибок равны
Отсюда следует, что если, как обычно, p мало по сравнению с длиной блока n (это означает, что произведение np мало), то множественные ошибки гораздо менее вероятны, чем одиночные ошибки.Выбор длины n для заданной вероятности p является инженерным решением.
Если n мало, то у вас будет больше избыточности (отношение числа отправленных битов к минимально возможному количеству битов n/(n-1)) чем при большем n, но если np велико, то избыточность будет небольшой.
но более высокая вероятность не обнаружить ошибку.
Вы должны принять инженерное решение о том, как сбалансировать эти два эффекта.
Если обнаружена одна ошибка, вы можете попросить отправить сообщение повторно, ожидая правильного результата во второй раз, в третий и так далее.
Однако если сохраненное сообщение неверно, вы будете запрашивать повторную передачу до тех пор, пока не произойдет другая ошибка, и у вас могут быть две необнаруженные ошибки в одной схеме обнаружения ошибок.
Таким образом, повторные передачи должны зависеть от ожидаемого характера ошибок.
Такие коды широко использовались еще во времена реле.
Телефонная компания использовала код 2 из 5 в центральных офисах и первых ретрансляторах, что означало, что только 2 из 5 реле были во включенном положении.
Этот код использовался для представления десятичной цифры, поскольку C(5, 2)=10. Если не ровно 2 реле были во включенном положении, это означало ошибку и повторялось.
Был также код 3 из 7, по-видимому, код нечетной четности.
Впервые я познакомился с этими кодами 2 из 5, когда использовал релейный компьютер модели 5 в Bell Labs, и был впечатлен не только тем, насколько они полезны в получении правильного ответа, но, что, на мой взгляд, что более важно, тем, как они дало техническим специалистам возможность реально обслуживать машины.
Любая ошибка обнаруживалась машиной практически в момент ее совершения, и потому указывала технику в правильном направлении, а не водила его за нос, заставляя менять настройки правильно работающих деталей в попытке найти неисправность.
Нарушая временную последовательность повествования, но сохраняя идеологический порядок, компания AT&T (прим.
американский транснациональный телекоммуникационный конгломерат) однажды спросила меня, как пользоваться кодированием, если люди используют алфавит из 26 букв, 10 десятичных цифр и пробела.
Это типично для наименования инвентаря, наименования частей и многих других наименований, включая наименование зданий.
Из данных об ошибках набора номера и из длительного опыта программирования я знал, что люди имеют сильную склонность переставлять соседние цифры: 67 может стать 76, а также заменять отдельные цифры (обычно удваивая цифру: 556, вероятно, станет 566).
Таким образом, обнаружения разовых ошибок недостаточно.
Я привел в конференц-зал двух очень способных людей и задал им вопрос.
Я отвергал предложение за предложением как недостаточно хорошее, пока, наконец, один из них, доктор Гилберт, не придумал продуманный кодекс.
В частности, он предложил обозначать символы 0, 1,.
9, А, В,.
, Z, а пространство цифрами 0, 1, 2,.
36. Тогда он вычислял не сумму значений, а то, является ли k-й символ имел значение (отмечено для удобства) Sk, то для сообщения из n символов вычисляем
«По модулю» здесь означает, что взвешенная сумма делится на 37 и используется только остаток.Чтобы закодировать сообщение из n символов, оставьте первый символ, k=1, пустым, а если значение остатка меньше 37, вычтите его из 37 и используйте соответствующий тестовый символ для помещения в первую позицию.
Таким образом, все сообщение с контрольным символом в первой позиции будет иметь контрольную сумму, равную 0. Если вы рассмотрите возможность замены любых двух разных символов или замены одного символа, вы заметите, что это нарушит взвешенную проверку четности по модулю 37 ( при условии, что заменяемые символы не разделены 37 символами).
Не вдаваясь в подробности, отметим, что важно, чтобы модуль был простым числом, которым является 37. Чтобы получить взвешенную сумму символов (фактически их значений), можно при желании отказаться от произведений и использовать только сложения и вычитания.
Поместите символы в столбец по порядку и вычислите промежуточные итоги, затем промежуточные итоги по модулю 37, затем прибавьте это к 37, и вы получите символ проверки.
В качестве иллюстрации используйте w, x, y, z.
На принимающей стороне вы многократно вычитаете модуль, пока не получите либо a-0 (допустимый символ), либо a – отрицательное число (недопустимый символ).Если вам нужно использовать эту кодировку, например, для наименования инвентаря, то если неправильное имя появится впервые при переносе, если не раньше (возможно, в предварительном процессе), то ошибка будет обнаружена, вы не приходится ждать, пока заказ будет доставлен в штаб-квартиру, а затем сообщать, что товара не существует, или получить неверный заказ.
Ошибка будет обнаружена до того, как заказ покинет вас, и поэтому ее можно легко исправить.
Только? Да! Ээффективно против человеческих ошибок (в отличие от примера с белым шумом), да! Действительно, в наши дни аналогичный код можно увидеть на книгах с номером ISBN. Это тот же код, только в нем используются 10 десятичных цифр, а число 10 не является простым числом, поэтому пришлось ввести 11-й икс, который может иногда появляться при проверке четности - действительно, примерно в каждой 11-й книге будет X в качестве последнего символа номера ISBN для проверки четности.
Тире в основном выполняют декоративную функцию и не используются в кодировании.
Проверьте это сами в своих учебниках.
Многие другие крупные организации могли бы с пользой использовать такие кодексы, если бы захотели приложить к этому усилия.
Я много раз указывал, что считаю, что в будущем информация в виде символов будет важна, а материальные вещи станут менее важными, и поэтому теория кодирования информации в пригодные для использования коды является нетривиальной темой.
В приведенном выше материале представлен простой код обнаружения ошибок для машин и продуманный код для использования человеком.
Это всего лишь два примера того, как теория кодирования может помочь в ситуациях, когда возможны машинные и человеческие ошибки.
Когда вы думаете об интерфейсе человек-компьютер, одна из вещей, которая может пригодиться, — это необходимость совершать как можно меньше человеческих нажатий клавиш — замаскированное кодирование Хаффмана! Очевидно, что учитывая вероятности различных ветвей в меню программы, можно при желании придумать способ уменьшить общее количество нажатий клавиш.
Таким образом, один и тот же набор меню можно настроить в соответствии с привычками разных людей, а не предлагать всем одинаковый интерфейс.
В более широком смысле «компьютерное программирование» на языках высокого уровня — это попытка добиться чего-то вроде кодирования Хаффмана, используя относительно небольшое количество нажатий клавиш для выполнения желаемых задач и используя разные клавиши для других задач.
Продолжение следует. Кто хочет помочь с переводом, версткой и публикацией книги - пишите в личное сообщение или на почту [email protected] Кстати, мы еще запустили перевод еще одной крутой книги - «Машина мечты: история компьютерной революции» ) Содержание книги и переведенные главы Предисловие
Кто хочет помочь с переводом, версткой и публикацией книги - пишите в личное сообщение или на почту [email protected]
- Введение в искусство заниматься наукой и инженерией: научиться учиться (28 марта 1995 г.
- «Основы цифровой (дискретной) революции» (30 марта 1995 г.
- «История компьютеров — аппаратное обеспечение» (31 марта 1995 г.
) Глава 3. История компьютеров — Аппаратное обеспечение
- «История компьютеров - Программное обеспечение» (4 апреля 1995 г.
- «История компьютеров – приложения» (6 апреля 1995 г.
) Глава 5: История компьютеров – практическое применение
- «Искусственный интеллект. Часть I» (7 апреля 1995 г.
) Глава 6. Искусственный интеллект - 1
- «Искусственный интеллект. Часть II» (11 апреля 1995 г.
) Глава 7. Искусственный интеллект – II
- «Искусственный интеллект III» (13 апреля 1995 г.
- «Н-мерное пространство» (14 апреля 1995 г.
- «Теория кодирования.
Представление информации, часть I» (18 апреля 1995 г.
) (переводчик отсутствует :((( )
- «Теория кодирования.
Представление информации, часть II» (20 апреля 1995 г.
)
- «Коды, исправляющие ошибки» (21 апреля 1995 г.
) (готовый)
- «Теория информации» (25 апреля 1995 г.
) (переводчик отсутствует :((( )
- «Цифровые фильтры, часть I» (27 апреля 1995 г.
) Глава 14. Цифровые фильтры - 1
- «Цифровые фильтры, часть II» (28 апреля 1995 г.
) Глава 15. Цифровые фильтры - 2
- «Цифровые фильтры, часть III» (2 мая 1995 г.
) Глава 16. Цифровые фильтры - 3
- «Цифровые фильтры, часть IV» (4 мая 1995 г.
) Глава 17. Цифровые фильтры – IV
- «Моделирование, часть I» (5 мая 1995 г.
) (в ходе выполнения)
- «Моделирование, часть II» (9 мая 1995 г.
) Глава 19. Моделирование - II
- «Моделирование, часть III» (11 мая 1995 г.
)
- «Волоконная оптика» (12 мая 1995 г.
) Глава 21. Волоконная оптика
- «Компьютерное обучение» (16 мая 1995 г.
) (переводчик отсутствует :((( )
- «Математика» (18 мая 1995 г.
- «Квантовая механика» (19 мая 1995 г.
- «Творчество» (23 мая 1995 г.
).
Перевод: Глава 25. Творчество
- «Эксперты» (25 мая 1995 г.
- «Недостоверные данные» (26 мая 1995 г.
) Глава 27. Недостоверные данные
- «Системная инженерия» (30 мая 1995 г.
- «Вы получаете то, что измеряете» (1 июня 1995 г.
- «Откуда мы знаем то, что знаем» (2 июня 1995 г.
) переводчик отсутствует :(((
- Хэмминг, «Вы и ваши исследования» (6 июня 1995 г.
).

-
Тайны Колеса Дракона
19 Oct, 24 -
Выбор Ноутбука Acer
19 Oct, 24 -
Обзор Surveylot — Стоит Ли Оно Того?
19 Oct, 24 -
«Нет Такой Профессии — Smm-Специалист»
19 Oct, 24 -
Рефлекс
19 Oct, 24