Решение Задачи Коммивояжера Методом Ветвей И Границ.

Привет, Хабр! При реализации различных алгоритмов для поиска гамильтониана с наименьшей стоимостью я столкнулся с публикация , предлагая свой вариант. Попробовав, я получил неправильный ответ: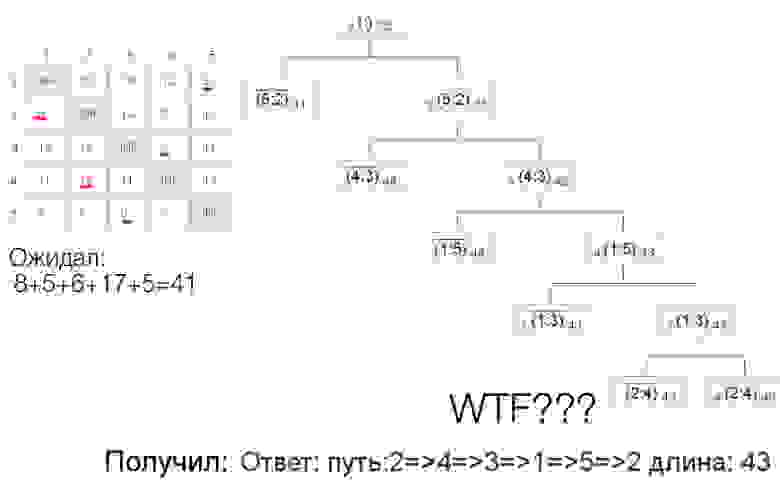

Решение задачи коммивояжера методом ветвей и границ.


Дальнейшие поиски в Интернете не принесли ожидаемого результата: либо теоретическое описание, сложное для нематематиков, либо понятное, но с ошибками.

Ниже под катом вы найдете исправленный алгоритм и онлайн-калькулятор.

Сам метод, опубликованный Литтлом, Мерти, Суини, Карелом в 1963 году, применим ко многим NP-полным задачам и представляет собой очень теоретический материал, который без хорошего знания английского языка и математики нельзя немедленно применить к нашей задаче о коммивояжере.

Коротко о методе – это полный перебор всех возможных вариантов с исключением явно неоптимальных решений.

Исправлен алгоритм поиска действительно минимального маршрута.

Алгоритм состоит из двух этапов:

Начальная ступень

Сокращение матрицы стоимости и вычисление нижней оценки стоимости маршрута r. 1. Вычислить наименьший элемент в каждой строке (константа приведения для строки) 2. Переходим к новой матрице затрат, вычитая из каждой строки ее константу приведения.

3. Вычислить наименьший элемент в каждом столбце (константа приведения для столбца) 4. Переходим к новой матрице затрат, вычитая из каждого столбца ее константу приведения.

В результате мы имеем матрицу затрат, в которой каждая строка и каждый столбец имеет хотя бы один нулевой элемент. 5. Границу на этом этапе рассчитываем как сумму констант приведения для столбцов и строк (эта граница и будет стоимостью, ниже которой невозможно построить требуемый маршрут)

Второй (основной) этап

1. Расчет штрафа за неиспользование для каждого нулевого элемента заданной матрицы затрат. Штраф за неиспользование элемента с индексом (h,k) в матрице означает, что это ребро не включено в наш маршрут, а значит, минимальная стоимость «неиспользования» этого ребра равна сумме минимальных элементов в матрице.

строка h и столбец k. а) Ищем все нулевые элементы в данной матрице б) Для каждого из них рассчитаем свой штраф за неиспользование.

в) Выберите элемент, соответствующий максимальному наказанию (любой, если их несколько) 2. Теперь разобьем наше множество S на множества, содержащие ребро с максимальным штрафом (S_ш ) и не содержащие этого ребра(S_без ).

3. Расчет сметы расходов по маршрутам, входящим в каждый из этих наборов.

а) Для множества S_без все просто: поскольку мы не берем соответствующее ребро с максимальным штрафом (h,k), то оценка стоимости для него равна оценке стоимости множества S + штраф за неиспользование ребра (h,k ) б) При расчете затрат на набор S_ш Учтем, что поскольку в маршрут включено ребро (h,k), то это означает, что ребро (k,h) не может быть включено в маршрут, поэтому в матрице стоимости пишем c(k,h)=бесконечность, и поскольку из точки h мы «уже вышли», а в точку k мы «уже дошли», то ни одно ребро, выходящее из h, и ни одно ребро, пришедшее в k, уже не может быть использовано, поэтому удаляем строку h и столбец k из матрицы затрат. После этого представляем матрицу, а затем смету затрат на S_ш равен сумме оценок стоимости для S и r(h,k), где r(h,k) — сумма констант приведения для модифицированной матрицы стоимости.

4. От каждый из неразделенных множеств выбирается тот, у которого наименьший балл.

Продолжаем так до тех пор, пока в матрице затрат не останется одна непересекающаяся строка и один неперечеркнутый столбец.

Незначительная оптимизация — добавление эвристики Да, действительно, почему бы нам не ввести эвристику? Ведь в алгоритме ветвей и границ мы фактически строим дерево, в узлах которого решаем брать ребро (h,k) или нет, и вешаем двух потомков — Sw(h,k) и Sw/o( ч,к).

Но мы выбираем лучший вариант для следующей итерации только на основе оценки.

Итак, выберем лучший не только по рейтингу, но и по глубине дерева, потому что.

Чем глубже выбранный элемент, тем ближе он к концу отсчета.

Таким образом, мы наконец можем дождаться ответа.

Теперь, собственно, об ошибках в той публикации

Была только одна ошибка — выбирать для разбиения множества с минимальной границей следует из всех возможных путей, а не из двух потомков, полученных в результате последнего разбиения.

Доказательство

Вернемся к картинке в начале поста:

Решение задачи коммивояжера методом ветвей и границ.

А вот решение с исправленным алгоритмом:

Решение задачи коммивояжера методом ветвей и границ.

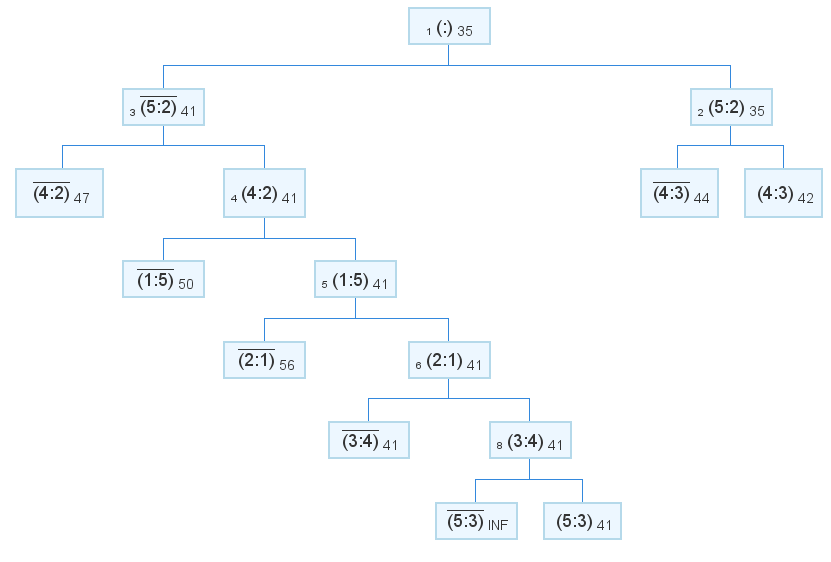
Ответ: путь:3=> 4=> 2=> 1=> 5=> 3 длина: 41 Как видите, включать в решение перевес 5:2 было бы ошибкой.

К.

Д.

График, сравнивающий метод ветвей и границ и время, затрачиваемое на случайную таблицу размером от 5x5 до 10x10: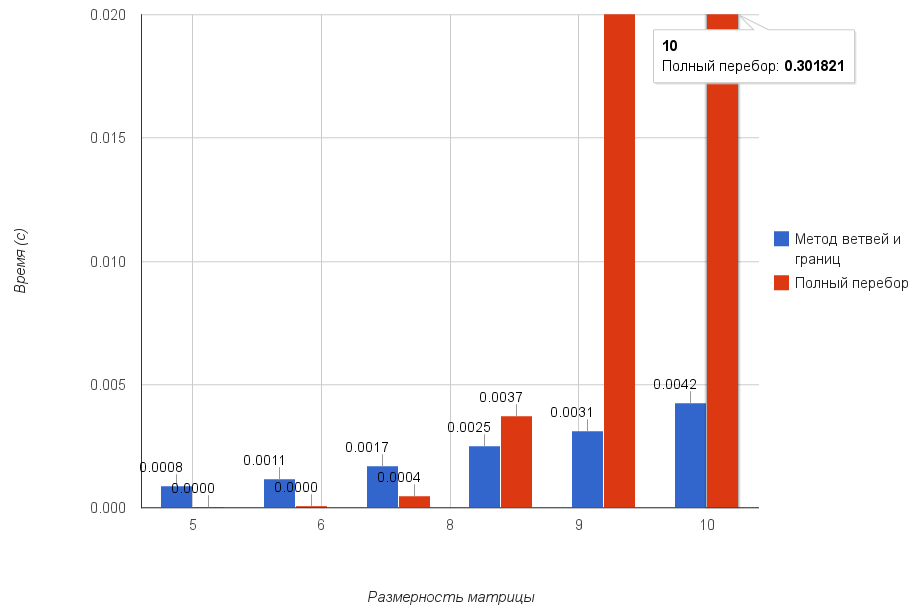

Решение задачи коммивояжера методом ветвей и границ.


График максимального и минимального затрачиваемого времени для матриц от 5х5 до 66х66.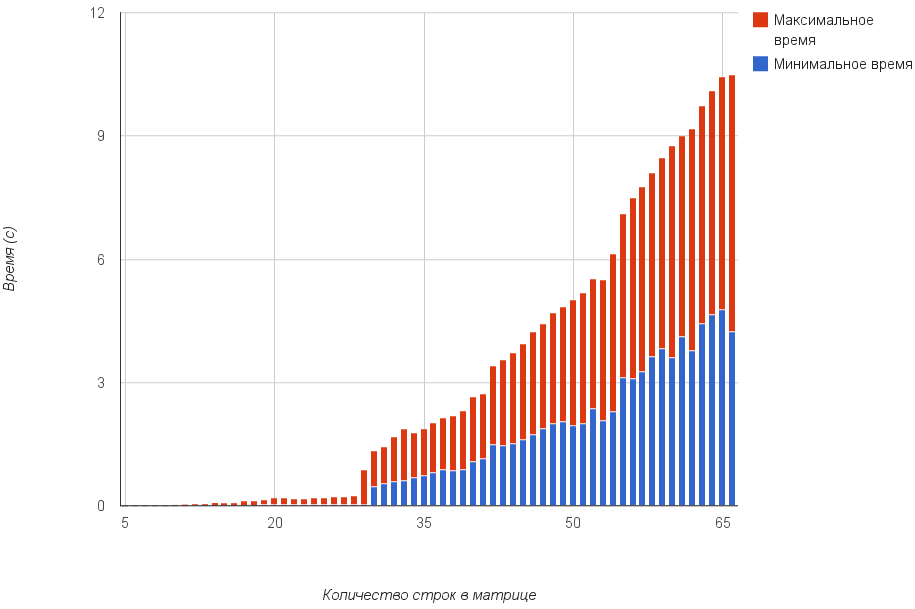

Вы можете попробовать подробное решение здесь .