Раньше облака в играх рисовались обычными 2D-спрайтами, которые всегда были повёрнуты в сторону камеры, но в последние годы новые модели видеокарт позволяют рисовать физически правильные облака без заметных потерь в производительности.
Считается, что студия Guerrilla Games привнесла в игры объёмные облака вместе с игрой Horizon Zero Dawn. Конечно, такие облака умели рендерить и раньше, но студия сформировала что-то вроде индустриального стандарта исходных ресурсов и используемых алгоритмов, и на данный момент любая реализация объёмных облаков так или иначе соответствует этому стандарту.
УПД.
Изображение обновлено.
Изменения описаны в конце статьи.

Весь процесс рендеринга облаков очень четко разделен на этапы и важно отметить, что неаккуратная реализация даже в одном из них может привести к таким последствиям, что будет непонятно, где ошибка и как ее исправить, поэтому желательно каждый раз делать контрольный вывод результата.
Отображение тонов, sRGB
Прежде чем приступить к работе с освещением, важно сделать две вещи:- Прежде чем вывести на экран итоговое изображение, примените хотя бы простейшую тональную компрессию:
Это необходимо, поскольку рассчитанные значения цвета будут намного больше единицы.tunedColor=color/(1+color)
- Убедитесь, что окончательный буфер кадров, который вы рисуете и который будет представлен на экране, имеет формат sRGB. Если есть проблемы с активацией режима sRGB, преобразование можно выполнить вручную в шейдере:
finalColor=pow(color, vec3(1.0/2.2))
Формула будет работать в большинстве случаев, но не на 100% в зависимости от монитора.Важно, чтобы преобразование sRGB всегда выполнялось последним.
Модель освещения
Рассмотрим пространство, заполненное частично прозрачным веществом разной плотности.Когда луч света проходит через такое вещество, он подвергается четырем эффектам: поглощению, рассеянию, усилению рассеяния и самоизлучению.
Последняя возникает при химических процессах, происходящих в веществе, и здесь не затрагивается.
Допустим, у нас есть луч света, который проходит через вещество из точки А в точку Б: 
Поглощение
Свет, проходящий через вещество, поглощается этим самым веществом.
Непоглощенную долю света можно найти по формуле:
Где
— свет, оставшийся после поглощения в точке
.
— точка на отрезке АВ на расстоянии
из.
Диффузия Часть света меняет свое направление под воздействием частиц вещества.
Долю света, не изменившую своего направления, можно найти по формуле:
Где
- доля света, не изменившая своего направления после рассеяния в точке
.
Поглощение и диссипация должны сочетаться:
Функция
называется ослаблением или угасанием.
Функция
- функция передачи.
Он показывает, сколько света останется при переходе из точки А в точку Б.
Касательно
И
:
, где C — некая константа, которая может иметь разное значение для каждого канала в RGB,
— плотность среды в точке
.
Теперь усложним задачу.
Свет движется из точки А в точку Б, по мере движения он тускнеет. В точке Х часть света рассеивается в разные стороны, одно из направлений соответствует наблюдателю в точке О.
Далее часть рассеянного света перемещается из точки Х в точку О и снова затухает. Интересующий нас путь света — AXO. 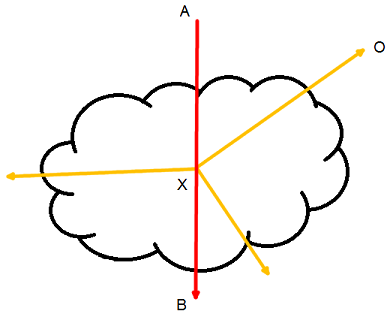
Мы знаем потерю света при движении от А к Х:
, так же, как мы знаем потерю света от Х до О - это
.
А как насчет доли света, которая рассеется в направлении наблюдателя? Улучшенное рассеяние Если при обычном рассеянии интенсивность света уменьшается, то при усиленном рассеянии она увеличивается за счет рассеяния света, происходящего на соседних участках.
Общее количество света, поступающего из соседних регионов, можно найти по формуле:
Где
означает взятие интеграла по сфере,
— фазовая функция,
- свет, идущий с определенного направления
.
Сосчитать свет со всех сторон довольно сложно, однако мы знаем, что основную часть света несет наш первоначальный луч АВ.
Формулу можно существенно упростить:
Где
— угол между лучом света и лучом наблюдателя (т. е.
угол AXO),
— начальное значение силы света.
Суммируя все вышесказанное, получаем формулу:
Где
- входящий свет,
- свет, достигающий наблюдателя.
Еще немного усложним задачу.
Допустим, свет излучается источником света направленного типа, то есть солнцем: 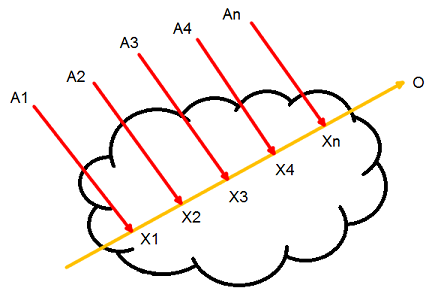
Происходит то же самое, что и в предыдущем случае, но много раз.
Свет из точки А1 рассеивается в точке Х1 в сторону наблюдателя в точке О, свет из точки А2 рассеивается в точке Х2 в сторону наблюдателя в точке О и т. д. Мы видим, что свет, достигающий наблюдателя, равен сумме:
Или более точное интегральное выражение:
Важно понимать, что здесь
, т.е.
отрезок разбит на бесконечное число участков нулевой длины.
Небо
При небольшом упрощении солнечный луч, проходя через атмосферу, испытывает лишь рассеяние, т.е.
.
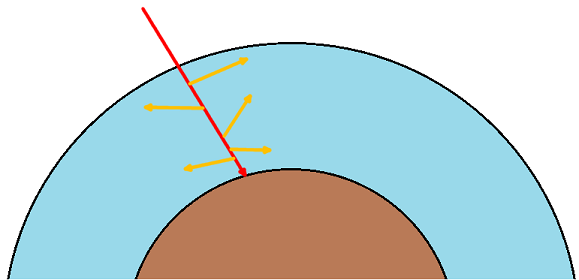
И даже не один тип рассеяния, а целых два типа: рэлеевское рассеяние и рассеяние Ми.
Первый вызван молекулами воздуха, а второй водным аэрозолем.
Общая плотность воздуха (или аэрозоля), через который пройдет луч света, двигаясь из точки А в точку Б:
Где
— высота масштабирования, h — текущая высота.
Простое решение интеграла будет:
где dh — размер шага, с которым производится выборка высоты.
Теперь посмотрим на рисунок и воспользуемся формулой, полученной в предыдущей части «модель освещения»: 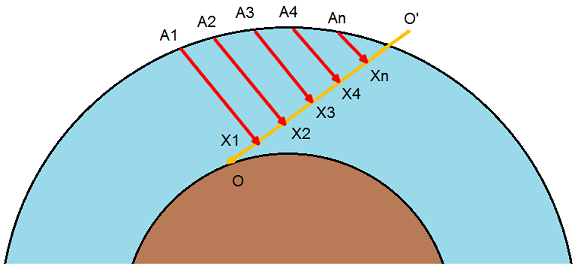
Наблюдатель смотрит от О к О'.
Мы хотим собрать весь свет, который дойдет до точек X1, X2,.
, Xn, рассеется в них, а затем достигнет наблюдателя:
Где
интенсивность света, излучаемого солнцем,
— высота в точке
; в случае неба константа C, находящаяся в функции
обозначается как
.
Решением интеграла может быть:
Эта формула справедлива как для рассеяния Рэлея, так и для рассеяния Ми.
В результате значения освещенности для каждого из рассеяний просто складываются:
Рэлеевское рассеяние
(содержит значения для каждого канала RGB)
Результат: 
Рассеяние Ми
(значения для всех каналов RGB одинаковы)
Результат: 
Количество образцов на сегмент
и на сегменте
можно брать 32 и выше.
Радиус Земли 6 371 000 м, толщина атмосферы 100 000 м.
Что со всем этим делать:
- В каждом пикселе экрана вычисляем направление наблюдателя V
- Позицию наблюдателя O примем равной {0,6371000,0}.
- Мы нашли
в результате пересечения луча, исходящего из точки О, и направления V и сферы с центром в точке {0,0,0} и радиусом 6471000 - Отрезок
разделен на 32 секции одинаковой длины - Для каждого раздела мы вычисляем рассеяние Рэлея и рассеяние Ми и все суммируем.
Более того, для расчета
нам также нужно разделить сегмент
в каждом случае на 32 равные секции.
можно прочитать через переменную, значение которой увеличивается на каждом шаге цикла.

Облачная модель
Нам понадобится несколько типов шума в 3D. Первый — это мозаичный фрактальный броуновский шум Перлина (fBm): Результат для 2D-среза:
Второй — скрытый шум Вороного fBm. Результат для 2D-среза:

Чтобы получить мозаичный шум Вороного fBm, необходимо инвертировать мозаичный шум Вороного fBm. Однако я немного изменил диапазоны значений на свое усмотрение:
float fbmTiledWorley3(.
)
{
return clamp((1.0-fbmTiledVoronoi3(.
))*1.5-0.25, 0.0, 1.0);
}
Результат сразу напоминает облачные структуры:

Для облаков вам нужно получить две специальные текстуры.
Первый имеет размер 128х128х128 и отвечает за низкочастотный шум, второй имеет размер 32х32х32 и отвечает за высокочастотный шум.
Каждая текстура использует только один канал в формате R8. В некоторых примерах используются 4 канала R8G8B8A8 для первой текстуры и три канала R8G8B8 для второй, а затем смешиваются каналы в шейдере.
Я не вижу в этом смысла, ведь смешивание можно сделать заранее, тем самым получив большую когерентность кэша.
Для смешивания, а также в некоторых других местах будет использоваться функция remap(), которая масштабирует значения из одного диапазона в другой: float remap(float value, float minValue, float maxValue, float newMinValue, float newMaxValue)
{
return newMinValue+(value-minValue)/(maxValue-minValue)*(newMaxValue-newMinValue);
}
Начнем подготовку текстуры с низкочастотным шумом:
R-канал — скрытый шум Перлина fBm
G-канал – скрытый шум ФБМ Ворли
B-канал — мозаичный шум Уорли fBm с меньшим масштабом
A-канал — тайловый fBm шум Ворли с еще меньшим масштабом 
Смешивание производится следующим образом: finalValue=remap(noise.x, (noise.y * 0.625 + noise.z*0.25 + noise.w * 0.125)-1, 1, 0, 1)
Результат для 2D-среза: 
Теперь готовим текстуру с высокочастотным шумом:
R-канал – скрытый шум ФБМ Ворли
G-канал — мозаичный шум Уорли fBm с меньшим масштабом
B-канал — тайловый fBm шум Ворли с еще меньшим масштабом 
finalValue=noise.x * 0.625 + noise.y*0.25 + noise.z * 0.125;
Результат для 2D-среза: 
Также нам понадобится 2D-текстура-карта погоды, которая будет определять наличие, плотность и форму облаков в зависимости от пространственных координат. Художники рисуют его, чтобы точнее откорректировать облачность.
Трактовка цветовых каналов карты погоды может быть разной, в том варианте, который я позаимствовал, она следующая: 
R-канал – облачность на малой высоте
G-канал – облачность на большой высоте
B-канал – максимальная высота облаков
А-канал – плотность облаков
Теперь мы готовы написать функцию, которая будет возвращать плотность облаков в зависимости от координат 3D-пространства.
На входе точка пространства с координатами в км.
vec3 position
Сразу добавим смещение ветром position.xz+=vec2(0.2f)*ufmParams.time;
Получение значений карты погоды vec4 weather=textureLod(ufmWeatherMap, position.xz/4096.0f, 0);
Получаем процент высоты (от 0 до 1) float height=cloudGetHeight(position);
Добавьте небольшое закругление облаков ниже: float SRb=clamp(remap(height, 0, 0.07, 0, 1), 0, 1);
Делаем линейное уменьшение плотности до 0 с увеличением высоты по B-каналу карты погоды: float SRt=clamp(remap(height, weather.b*0.2, weather.b, 1, 0), 0, 1);
Объединяем результат: float SA=SRb*SRt;
Еще раз добавьте закругление облаков ниже: float DRb=height*clamp(remap(height, 0, 0.15, 0, 1), 0, 1);
Также добавляем закругление облаков вверху: float DRt=height*clamp(remap(height, 0.9, 1, 1, 0), 0, 1);
Совмещаем результат, и сюда добавляем влияние плотности с карты погоды и влияние плотности, которая задается через gui: float DA=DRb*DRt*weather.a*2*ufmProperties.density;
Соединяем низкочастотный и высокочастотный шум из наших текстур: float SNsample=textureLod(ufmLowFreqNoiseTexture, position/48.0f, 0).
x*0.85f+textureLod(ufmHighFreqNoiseTexture, position/4.8f, 0).
x*0.15f;
Все документы, которые я читал, имеют разные способы слияния, но этот мне понравился.
Определяем степень покрытия (% неба, занятого облаками), которая задается через gui; Также используются R-, G- каналы карты погоды: float WMc=max(weather.r, clamp(ufmProperties.coverage-0.5, 0, 1)*weather.g*2);
Рассчитаем конечную плотность: float d=clamp(remap(SNsample*SA, 1-ufmProperties.coverage*WMc, 1, 0, 1), 0, 1)*DA;
Вся функция: float cloudSampleDensity(vec3 position)
{
Теги: #Разработка игр #математика #Алгоритмы #программирование #Работа с 3D-графикой #объемный рендеринг #шум Перлина #физически обоснованный рендеринг #реалистичные облака #реалистичное небо #Horizon Zero Dawn

-
Медведев Заставил Губернаторов Вести Блоги
19 Oct, 24 -
Вечные
19 Oct, 24 -
Google Код Закрывается
19 Oct, 24 -
Автофокус На Директе: Первые Результаты
19 Oct, 24


