Начинается время вступительных экзаменов, а значит и время решения интересных задач.
Несколько лет назад Центр компьютерных наук предложил абитуриентам разобраться с задачей про граф кактус, и сегодня мы о ней поговорим.
Попробуйте сами подумать о проблеме, а затем проверьте решение.
Кстати, набор в центр CS это уже происходит. В этом году поступить на очную форму обучения можно не только в Санкт-Петербурге, но и в Новосибирске.
Приходите – на занятиях будет еще больше интересного.
Еще немного о Центре CS и подборе персонала Центр компьютерных наук — совместная инициатива Клуб компьютерных наук в ПОМИ , компании JetBrains И Школы анализа данных Яндекса .
Центр предлагает двух- или трехгодичные курсы для студентов, аспирантов и выпускников технических вузов, а также молодых специалистов, желающих развиваться в сфере анализа данных, разработки программного обеспечения или теоретической информатики.
Занятия проходят по вечерам в Санкт-Петербурге или Новосибирске.
В 2017 году набор на очную форму обучения состоит из четырех этапов:
- подача заявки до 16 апреля включительно,
- онлайн-тестирование,
- экзамен,
- очное интервью.
Задача
Кактус — это простой связный граф, в котором любые два цикла имеют не более одной общей вершины.
Докажите, что максимальное количество ребер в кактусе с n вершинами равно
.
*
- округление в меньшую сторону.
Решение
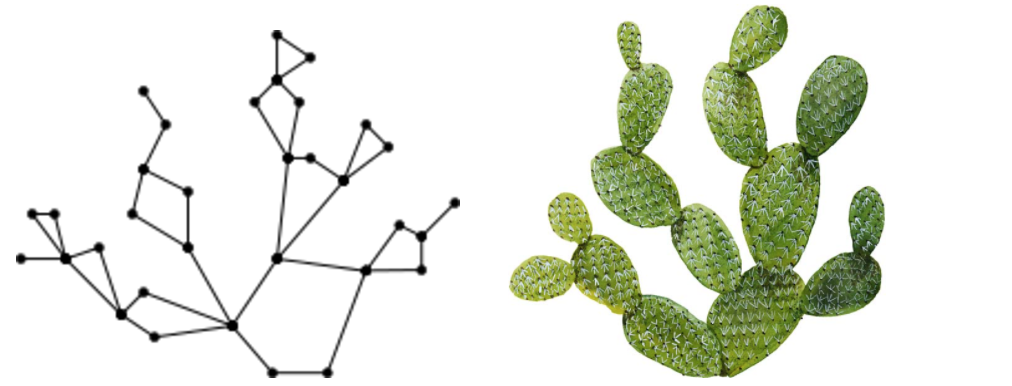
Для начала нужно понять, как устроен этот график.В этом нам поможет пример графика, представленного на рисунке.
Рядом с ним настоящий кактус.
Это позволяет понять, почему дано такое название.
Любой цикл, имеющий более трех вершин, можно «ужечь», заменив его циклом длины три и простым путем.
При этом общее количество вершин и ребер в графе не изменится, а сам граф останется кактусом.
Ниже приведен пример «затягивания» графика.
Теперь рассмотрим кактус, у которого есть ребра, не лежащие ни на одном цикле.
Любые два таких ребра можно свернуть в вершину.
В результате из графа исчезнут два ребра и две вершины.
Затем добавьте в граф цикл длины три, одна из вершин которого будет уже существующей вершиной графа.
Количество вершин останется прежним, а количество ребер увеличится на одно.

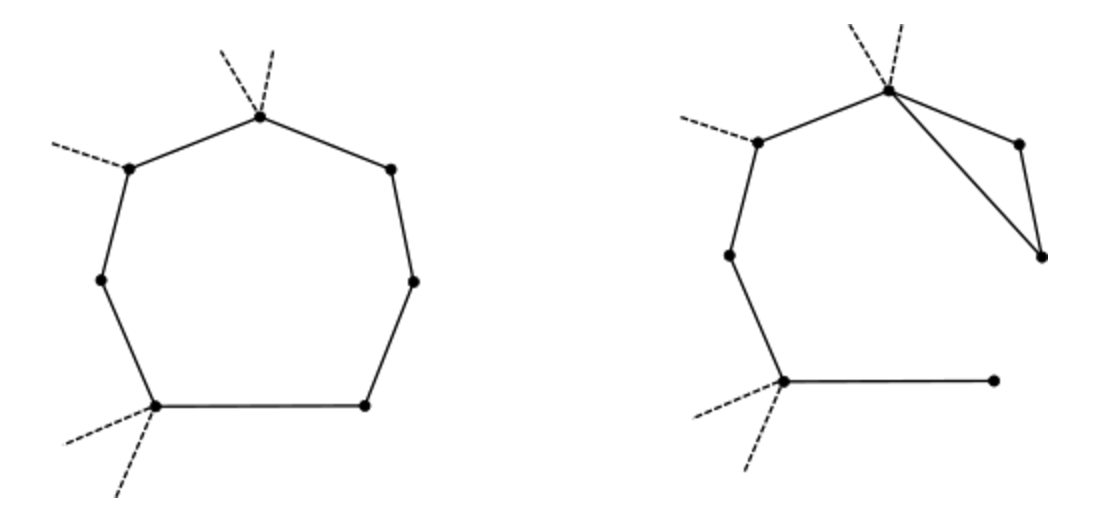
На рисунке выше показан пример описанной выше манипуляции.
На левом рисунке изображен кактус, у которого выделены края вне циклов.
На центральной картине тот же кактус, но с подтянутыми ребрами.
Мало того, что исчезли два ребра, так еще и вершин стало на две меньше.
И, наконец, на правой картинке изображен кактус, к которому мы добавили еще один треугольник — появились три новых ребра и две вершины.
В результате количество вершин до и после операции не изменилось, но количество ребер увеличилось.
Таким образом, максимальное количество ребер в кактусе достигается тогда, когда он целиком состоит из треугольников и, возможно, одного ребра, не лежащего ни в одном цикле.
Такой кактус можно построить, последовательно добавляя внешние треугольные блоки, начиная с любого
или с
, в зависимости от паритета
.
(
- полный график на
вершин.
) При добавлении каждого блока добавляются две вершины и три ребра, из чего сразу следует требуемое в задаче утверждение.
Теги: #математика #центр КС
-
Сохраните Свои Фишки И Получите Автобус!
19 Oct, 24 -
Получите Максимум От Outlook Express
19 Oct, 24 -
Приобретения Google С 2001 По 2007 Год
19 Oct, 24 -
Симфония
19 Oct, 24


