Два плюс два, умножить на два? Не знаю, как вы, а я долго боролся в школе, пытаясь выяснить приоритет операций и скобок.
Затем, как и каждый новый программист, при написании собственного калькулятора я боролся с приоритетом операторов и круглыми скобками.
Но оказалось, что все эти мучения были напрасны.
Ведь есть замечательный механизм, известный как обратная польская запись.
Я хочу рассказать вам, что это такое и как с этим работать.
В математике существует древняя традиция размещать оператор между операндами (x+y), а не после операндов (xy+).
Форма с оператором между операндами называется инфиксной записью.
Форма с оператором после операндов называется постфиксной, или обратной польской нотацией, в честь польского логика Ю.
Лукасевича (1958), изучавшего свойства этой нотации.
Обратная польская запись имеет ряд преимуществ перед инфиксной записью при выражении алгебраических формул.
Во-первых, любую формулу можно выразить без скобок.
Во-вторых, она удобен для расчета формул в машинах со стопками .
В-третьих, инфиксные операторы имеют произвольный и нежелательный приоритет. Например, мы знаем, что ab+c означает (ab)+c, а не a(b+c), потому что было произвольно определено, что умножение имеет приоритет над сложением.
Но имеет ли сдвиг влево приоритет над операцией AND? Кто знает? Обратная польская запись исключает подобные недоразумения.
Постановка задачи На вход программы поступает выражение, состоящее из односимвольных идентификаторов и знаков арифметических операций.
Вам необходимо преобразовать это выражение в обратную польскую запись или сообщить об ошибке.
Алгоритм перевода в обратную польскую запись Существует несколько алгоритмов преобразования инфиксных формул в обратную польскую запись.
Мы рассмотрим доработанный алгоритм, идею которого предложил?.
Дейкстра (E.W. Dijkstra).
Предположим, что формула состоит из переменных, операторов с двумя операндами +,-,*,/,^, а также левой и правой круглых скобок.
Чтобы отметить конец формулы, мы вставим символ после ее последнего символа и перед первым символом следующей формулы.
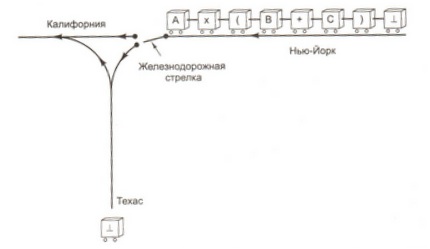
На рисунке схематически изображена железная дорога из Нью-Йорка в Калифорнию с ответвлением, ведущим в Техас.
Каждый символ формулы представлен одной кареткой.
Поезд движется на запад (слева).
Перед переключением каждая машина должна остановиться и выяснить, следует ли ей ехать прямо в Калифорнию или по пути ей придется остановиться в Техасе.
Автомобили, содержащие переменные, всегда едут в Калифорнию и никогда не едут в Техас.
Автомобили, содержащие все остальные символы, должны узнать о содержимом ближайшего автомобиля, следующего в Техас, прежде чем проехать через переключатель.
В таблице представлена зависимость ситуации от того, какая машина выехала в Техас последней и какая машина находится на стрелке.
Первая машина (отмеченная символом ⊥) всегда отправляется в Техас.

Цифры соответствуют следующим ситуациям:
1. Машинка-переключатель отправляется в Техас.
2. Последняя машина, направляющаяся в Техас, разворачивается и направляется в Калифорнию.
3. Машину переключения и последнюю машину, направляющуюся в Техас, угоняют и исчезают. 4. Стоп.
Символы на линии Калифорнии представляют формулу в обратной польской записи, если читать ее слева направо.
5. Стоп.
Произошла ошибка.
Исходная формула была неправильно сбалансирована После каждого действия производится новое сравнение между автомобилем, находящимся у переключателя (это может быть тот же автомобиль, что и в предыдущем сравнении, или это может быть следующий автомобиль) и автомобилем, который в данный момент последним выезжает в Техас.
.
Этот процесс продолжается до тех пор, пока не будет достигнут шаг 4. Обратите внимание, что линия до Техаса используется как стек, где отправка автомобиля в Техас помещает элемент в стек, а поворот автомобиля, отправленного в Техас в сторону Калифорнии, выталкивает элемент из стека.
Порядок переменных в инфиксной и постфиксной записи одинаков.
Однако порядок операторов не всегда одинаков.
В обратной польской записи операторы появляются в том порядке, в котором они будут выполняться.
Пример вычисления выражения в обратной польской записи Обратная польская нотация идеально подходит для вычисления формул на компьютере со стеком.
Формула состоит из n символов, каждый из которых является операндом или оператором.
Алгоритм расчета формулы в обратной польской записи с использованием стека прост. Вам просто нужно прочитать обратную польскую запись слева направо.
Если встречается операнд, его необходимо поместить в стек.
Если встречается оператор, необходимо выполнить указанную им операцию.
В качестве примера рассмотрим вычисление следующего выражения: (8+2*5)/(1+3*2-4).
Соответствующая формула в обратной польской записи выглядит так: 825*+132*+4-/ Число наверху стека — это правый операнд (а не левый).
Это очень важно для операций деления, вычитания и возведения в степень, поскольку порядок операндов в этом случае имеет значение (в отличие от операций сложения и умножения).
Другими словами, операция деления работает следующим образом: сначала в стек помещается числитель, затем знаменатель, а затем операция дает правильный результат. Обратите внимание, что преобразовать обратную польскую запись в машинный код очень просто: вам просто нужно следовать формуле в обратной польской записи, написав по одной команде для каждого символа.
Если символ является константой или переменной, нужно ввести команду для помещения этой константы или переменной в стек; если символ является оператором, необходимо ввести команду для выполнения этой операции.

P.S. Исходники, как всегда, вы можете скачать его на моем сайте , пока он не попадает под хабраэффект.
П.
П.
С.
Теперь каждый может написать свой калькулятор.
С блэкджеком и скобками.
Теги: #Алгоритмы #обратная польская запись #Алгоритмы

-
Краткое Описание Программы Ppc Coach
19 Oct, 24 -
Продукт Без Тестирования
19 Oct, 24 -
Борьба С Интернетом Вещей
19 Oct, 24


