Немного Финансовой Математики: Расчет Инфляции И Процентов

Недавно мне пришлось проверить расчеты, которые выполняют коммунальные предприятия моего города.

Возник спорный вопрос, решить который можно только проведя правильные расчеты.

Забегая вперед, скажу, что коммунальные предприятия мыслят неправильно.

Поэтому здесь мы рассмотрим, как правильно рассчитать расходы на инфляцию и 3% годовых по долговым обязательствам, согласно Гражданскому кодексу Украины.

В первой части описан расчет инфляционных издержек, это специфично для Украины.

Второй (б О Вторая часть будет посвящена вопросу расчета 3% годовых.

Также она применима к Российской Федерации, Республике Беларусь и Республике Казахстан, но в этих странах ставка не фиксированная, а зависит от ставки рефинансирования ЦБ.

На остальные страны я не смотрел.

Вторая часть очень близка к расчету процентов по обычным кредитным операциям (кредитам, авансам, займам и т.п.

).

Сначала теория, напоследок немного кода.

Все это под катом.

Итак, мне попался документ от работников ЖКХ «Справка о расчете расходов на инфляцию и 3% годовых».

Я проверил его и выяснил, что он рассчитан по неверному алгоритму и представляет интерес, так как должен реализовывать требования статьи Гражданского кодекса Украины.

Что необходимо учитывать, написано в Гражданском кодексе Украины:

Статья 625 Гражданского кодекса Украины.

«Ответственность за нарушение денежного обязательства» 2. Должник, просрочивший исполнение денежного обязательства, по требованию кредитора обязан уплатить сумму долга с учетом установленного показателя инфляции за весь период просрочки, а также 3% в год. в год просроченная сумма.

Инфляционные издержки

Инфляция – это процесс, характеризующийся обесцениванием валюты, то есть уменьшением ее покупательной способности и общим ростом цен.

Без учета инфляции окончательные результаты расчетов денежных потоков весьма условны.

Индекс инфляции (ИИ), или индекс потребительских цен (ИПЦ), Индекс потребительских цен (ИПЦ) — один из видов индексов цен, создаваемых для измерения среднего уровня цен на товары и услуги (потребительскую корзину) за определенный период в экономика.

ИИ – показатель, характеризующий динамику общего уровня цен на товары и услуги, приобретаемые населением для непроизводительного потребления.

Это индекс роста, который показывает, на какой процент в среднем выросли цены за рассматриваемый период. В Украине AI и CPI являются синонимами Поскольку индекс цен является цепным индексом, для последовательных периодов он рассчитывается путем умножения показателей, например, 101%*102%=(1,01*1,02)*100%=103,02%.

ИИ рассчитывается Государственным комитетом статистики Украины и публикуется в официальных периодических изданиях.

Эти показатели можно использовать для пересчета денежных сумм.

Что думают коммунальщики?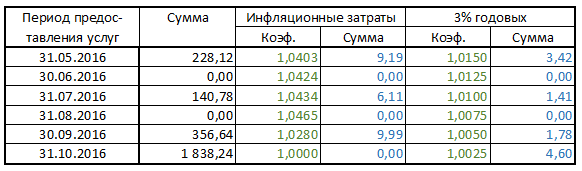



Последняя дата расчета – 7 декабря 2016 года.

Давайте разберемся, как коммунальные предприятия получили стоимостные коэффициенты инфляции? Невооруженным взглядом видно, что в третьем (и пятом столбце) вместо целой части 1 должна быть целая часть 0. Как они получили дробную часть? Сентябрь 2016. Дробная часть 0,028. Срок оплаты за сентябрь – 20 октября 2016 года.

Дробная часть соответствует опубликованному Госкомстатом индексу инфляции за октябрь 2016 года – 102,8%.

Август 2016. Дробная часть 0,0465. Срок оплаты за август – 20 сентября 2016 года.

Дробная часть соответствует индексу инфляции за сентябрь, умноженному на ИИ за октябрь: 101,8%*102,8%=104,65%, или в дробях 1,018*1,028=1,046504. Коммунальные предприятия округляют до 1,0465 и выводят это число, хотя одно следует вычесть, так как в следующем столбце они печатают только сумму инфляционных издержек, а не начисленную сумму.

Июль 2016 г.

и ранее.

Я провел эти расчеты и восстановил алгоритм.

Коммунальные услуги умножают индексы инфляции, начиная с месяца, следующего за месяцем оказания услуг (месяца оплаты) и заканчивая октябрем 2016 года.

Начальная точка верно лишь частично.

Как я покажу позже, в общем случае действительно нужно начинать расчет с этого месяца, но в нашем конкретном случае нужно пропустить первый месяц (приравнять ИИ к 100%).

Конечная точка умножение.

Так как последний день расчета в декабре, а закончить нужно в декабре, это в общем случае.

Как я покажу позже, в данном конкретном случае декабрь тоже нужно пропустить (тоже приравнивая AI к 100%).

А по состоянию на 7 декабря AI за декабрь еще не был опубликован.

Почему ноябрь нигде не учитывается? Я думаю, они просто забыли это ввести в систему.

Теперь посмотрим, как необходимый рассчитать индекс инфляции.

Как необходимый — описано в Информационном письме Высшего хозяйственного суда Украины № 01-06/928/2012 от 17 июля 2012 г.

[6].

Процитирую часть абзаца:

Сумма долга, которую необходимо оплатить с 1 по 15 число месяца, индексируется с учетом текущего месяца, а если сумма долга должна быть погашена с 16 по 31 число месяца, расчет начинается со следующего месяца.

Аналогично, если погашение долга производилось с 1 по 15 число месяца, то инфляционные издержки рассчитываются без учета этого месяца, а если с 16 по 31 число месяца, то инфляционные издержки рассчитываются с учетом этого.

месяц.

для оказания услуг в сентябре дата начала расчетов – 21 октября 2016 года, а срок – 7 декабря 2016 года.

Те.

Правильно считать так: для оказания услуг в сентябре 2016 года посчитайте инфляцию за три месяца (пройдите курсором или циклом), с октября по декабрь, но в первый и последний месяц примите ИИ равным 1 (100%) и учитывать только ноябрь.

На ноябрь 2016 года ИИ составил 101,8%, т.е.

коэффициент должен быть 0,0180, а не 0,0280. О ведущем подразделении я писал ранее.

3% годовых

Как я писал ранее, ведущей единицы быть не должно, должен быть 0. Смотрим на дробную часть, и замечаем, что она какая-то подозрительно круглая – каждый предыдущий месяц на 0,0025 больше текущего.

Путем несложных расчетов можно определить, что коммунальные предприятия, не мудрствуя лукаво, разделили 3% на 12 месяцев, получили 0,0025, или 0,25% в месяц, и начисляют этот процент за каждый полный и неполный месяц просрочки.

Да, если посмотреть на октябрь 2016 года, срок оплаты по которому был 21 ноября, а расчеты производились 7 декабря, то менее чем за полный месяц насчитали те же 0,25%.

Этот подход восхищает своей жестокой прямотой, но, как я покажу позже, финансовая математика не знает такого алгоритма.

Украинское законодательство и финансовая математика не дают однозначного ответа на вопрос, как посчитать 3% годовых? Я нашел несколько книг по этому вопросу, но книги древние, датированные 2002 годом.

Поэтому алгоритмы из книг будут дополнены тем, что нам удалось нагуглить из более современных и западных статей.

[1] была переиздана в 2007 году, и более поздние русскоязычные книги найти не удалось.

Возможно, потому, что финансовая математика как наука зародилась очень давно, задолго до появления компьютеров; такие понятия, как «кредит» и «заемный процент», возникли несколько сотен лет назад. И алгоритмы не сильно изменились с 2002 года.

Но западный взгляд на проблему отличается от того, который описан в русскоязычных книгах.

Информацию буду приводить сначала из русскоязычных книг, а затем из западных статей, указывая, где они совпадают. То, что написано ниже, относится к конкретному случаю расчета 3% годовых по долгу, но может быть обобщено и на расчет процентов по другим кредитным отношениям, если проценты рассчитываются по простым процентам, а не по сложным процентам.

Согласно ст. 625 ГК Украины, нужно начислять 3% в год по схеме простых процентов.

Для расчета суммы процентов сумму долга (или тело кредита, в общем случае) необходимо умножить на нормализованную годовую процентную ставку 3% и умножить на долю года (длительность в годах), в течение которой был просрочен.

Эта доля может быть больше 1, если просрочка составляет более года.

Продолжительность задержки выражается в днях.

В целом срок кредита Может быть выраженный в днях (здесь не рассматривается ситуация, когда срок кредита выражается в месяцах и годах).

А годовая ставка 3% — это нормализованная простая процентная ставка за год. Поэтому вам необходимо уметь конвертировать продолжительность просрочки (кредита) в днях в продолжительность в годах.

Это нетривиальная задача, поскольку от его числа зависит продолжительность года.

Продолжительность в днях — это однозначно определенная мера продолжительности календарных интервалов, в отличие от продолжительности в годах.

Определение последнего требует уточнения в виде правила перевода продолжительности в днях в длительность в годах.

Ряд стандартных методов перевода продолжительности в днях в продолжительность в годах основаны на делении количества дней на так называемую продолжительность.

«годовой делитель» .

Наиболее типичные значения годового делителя — 360 и 365 дней.

В простейших случаях делителем является постоянное число, не зависящее от отрезка.

Делимое (числитель дроби) всегда равно количеству дней в периоде.

И вам необходимо определиться с порядком исчисления сроков в днях.

Давайте посмотрим на два надуманных примера:

1. Клиент получает краткосрочный кредит от банка с 06.12.2018 по 07.12.2018. Какой срок договора и за сколько дней должны начисляться проценты? Очевидно - 1 день.

2. Абонент заказывает услугу заранее у оператора связи, со сроком действия в будущем с 06.12.2018 по 07.12.2018. Каков срок оказания услуги и за сколько дней вперед необходимо оплатить абонентскую плату за услугу? Очевидно, 2 дня.

• [12.06.2018 00.00.00, 12.07.2018 00.00.00) - здесь правая граница интервала не входит в интервал,
• [06.12.2018 00.00.00, 06.12.2018 23.59.59] - здесь в интервал входит правая граница интервала.

[4] говорит то же самое другими словами: «День выдачи кредита и день погашения считаются за один день».

Этот метод определяет так называемое точное время.

Также можно легко определить, относятся ли обе даты к одному и тому же году, и доступен ли календарь, показывающий порядковый номер каждого дня года.

Тогда достаточно от порядкового номера поздней даты вычесть порядковый номер ранней даты и результат даст продолжительность периода.

В базе данных Oracle вы можете просто вычитать даты (тип DATE), усеченные до дня (с отброшенным временем), друг из друга, при этом разница будет составлять целое число дней.

Во втором случае (2) речь идет о дне, поэтому мы считаем два дня.

Далее я исхожу из того, что количество дней вами уже определено, например, в случае с ЖКХ, когда срок оплаты 20 сентября (т. е.

это последний допустимый день оплаты), и платеж был произведен 21 сентября, т.е.

очевидно, что просрочку следует принять равной 1 дню.

Если вы встретите индикатор интервала, который не включает левую границу, просто переместите левую границу вправо на один день.

Как мы будем вычислять количество дней и числитель дроби? Существует точный подсчет и приблизительный подсчет.

Точный подсчет дней

русскоязычная практика

Выбор точного количества дней в периоде в качестве делителя и годового делителя 360 или 365 в качестве знаменателя определяется двумя наиболее распространенными правилами: Правило (R1) ACT/365. Для этого правила продолжительность в днях делится на число 365. Обратите внимание, что продолжительность високосного года будет равна 366/365 = 1,00274, что больше единицы.

Ошибка правила ACT/365 будет тем больше, чем больше високосных лет будет в периоде.

Следовательно, сумма 3% годовых, начисленная по этому правилу, составит более 3%.

Правило (R2) ACT/360. Это так называемое «Банковское правило», согласно которому продолжительность в днях делится на 360. Это правило еще больше увеличивает годовую длину интервалов.

Для невисокосного года его длина составит 365/360=1,01389, а для високосного 366/360=1,01667. Естественно, чем дольше период, тем больше степень «растянутости» в годах.

Это правило чаще всего используется в расчетах, касающихся денежного рынка, т.е.

рынка краткосрочных долговых обязательств, таких как банковские депозиты, векселя, коммерческие бумаги, депозитные сертификаты и т.п.

Значение 3% годовых за год будет даже больше, чем при использовании предыдущего правила.

Если годовой делитель принять равным 360 дням, проценты, полученные с помощью такого делителя, называются обычный , или коммерческий .

Если делитель принять равным 365 или, как я покажу позже, 366 дням, проценты называются точными.

Очевидно, что обычные проценты выше, чем точные.

Хотя первое правило точнее второго, оба они недостаточно точны.

Чтобы исключить влияние високосных годов на результат, есть еще два правила.

Правило (R3) ACT/365, Япония.

Расчет аналогичен правилу ACT/365, но при расчете длительности интервала (числителя дроби) исключаются високосные даты.

Годовой делитель остается неизменным.

Согласно Вики:

Во многих европейских странах до XVIII века 29 февраля считалось несуществующим днем, датой, не имеющей юридического статуса.

Часто в этот день не заключались сделки, не производились платежи, не выдавались кредиты и т. д. – в связи с тем, что возникали трудности с формальной стороной вопроса и разрешением дел в суде.

Правило (R4) ACT/ACT является базовым.

Разделим необходимый период на три части:

• первая часть, от даты начала до конца года, в котором находится дата начала,
• третья часть – от начала года, в котором находится дата окончания, до даты окончания,
• вторая часть - 0 или несколько полных календарных лет между первой и третьей частями.

Правило (R5) «Краткая» модификация ACT/ACT для периодов менее года.

В этом случае продолжительность в днях делится на годовой делитель 365 или 366 в зависимости от того, есть ли в искомом периоде дата 29 февраля? Особенностью короткого правила ACT/ACT является то, что если интервал не укладывается в календарный год (его концы принадлежат соседним годам), то применение основного и краткого правил приведет к разным результатам.

Западная практика

Часто одни и те же русскоязычные правила имеют разные названия, причем не по одному.

Приведенная ниже информация основана на [2].

Это Вики, я проверил все источники и использовал другую информацию из гугла: в правилах с точным количеством дней всё правильно, но в правилах с примерным количеством дней есть другие трактовки правил, и они часто меняются со временем, поэтому для применения правил на практике примерного количества дней в этой статье недостаточно.

Правило (W1) Фактический/Фактический ISDA. Это правило дает тот же результат, что и (R4) «ACT/ACT main», но формулируется иначе: интервал делится на високосные и невисокосные годы, независимо от того, полные они или неполные, затем суммируется сумма дней, попадающих в Високосные годы делятся на 365, а сумма дней в невисокосные годы делится на 366, два числа суммируются.

Другие названия правила в западной практике: Actual/Actual, Act/Act, Actual/365, Act/365. Да, фамилия такая же, как и у правила (R1), хотя суть правила другая.

Правило (W2) Фактическое/365 Фиксированное.

Это правило в точности повторяет правило (R1) ACT/365 – количество дней делится на 365. Другие названия правила в западной практике: Act/365Fixed, A/365Fixed, A/365F, англ.

Правило (W3) Фактически/360. Это правило такое же, как и (R2) ACT/360 — точное количество дней делится на 360. Правило (W4) Фактическое/364. Количество дней делится на 364. Не имеет аналога в русскоязычной практике.

Правило (W5) Фактический/365L. Состоит из двух подправил:

1. Для ежегодных платежей.

   Если внутри периода дата 29 февраля, то количество дней в периоде делится на годовой делитель 366, если нет – на 365. В этом смысле оно совпадает с правилом (R5) ACT/ACT «короткая модификация».

   .

2. Если частота выплат отличается от ежегодной.

   Если конечная дата приходится на високосный год (и не обязательно равна 29 февраля), то годовой делитель равен 366, иначе — 365. Аналога в русскоязычной практике он не имеет.

1. Основное, для периодов меньше года: Если дата 29 февраля находится внутри периода, то количество дней в периоде делится на годовой делитель 366, если нет - на 365. В этом смысле оно также совпадает с правилом (R5) ACT/ACT «короткая модификация».

2. Расширенный, для периодов продолжительностью более года: от даты окончания до даты начала отсчитывается целое число полных лет. Для остатков менее года применяется основное подправило.

   Суммируются количество полных лет и доля года по основному подправилу.

В данном случае за дату n лет назад следует принять 29 февраля.

Добавлю, что также возникает вопрос, если отсчет велся от 29 февраля, а количество полных лет назад не делится на четыре, и соответственно предыдущий год не был високосным.

Я не вдавался здесь в подробности.

Но вы можете обратиться к ссылкам из [2].

И вишенка на торте Правило (П7) 1/1. Количество дней делится на годовой делитель 365,25. Используется для расчетов, связанных с инфляцией.

Примерное количество дней

Однако иногда встречаются схемы, основанные на так называемом упрощенном, или приблизительном, счете дней.

Идея этих схем состоит в том, чтобы «выровнять» продолжительность всех месяцев до 30 дней.

Таким образом, год будет состоять из 12 месяцев по 30 дней, т. е.

из 360 дней.

Поэтому годовой делитель (знаменатель дроби) по этим правилам всегда будет равен 360, а числитель вычисляется особым образом.

Поскольку точное количество дней кредита в большинстве случаев, но, конечно, не всегда, больше примерного (что легко проверить, определив среднее количество дней в месяце за год, равное 30,44), метод расчета процентов с точным количеством дней кредита обычно дает больший рост, чем с кем-то из близких.

[4] Самый простой вариант этого правила, так называемый Основное правило 30/360 , описывается следующим образом (здесь и далее информация из книги [1] — русскоязычная практика): Основное правило – 30/360. Примерное количество дней между датами

 360 * (y2 – y1) + 30 * (m2 – m1) + (d2 – d1),

Это правило появилось еще до создания первых вычислительных устройств и существенно экономило затраты на вычислительные операции в финансовой практике.

Хотя сейчас необходимость в упрощенных методах отпала, тем не менее, утвердившись на практике, они по традиции иногда используются и в настоящее время.

Правило применяется с обязательной модификацией, которая определяет, как обрабатывать последние дни месяцев:

русскоязычная практика

Правило (R6) 30/360 ISDA. Если d1 = 31, то d1’ = 30, иначе d1’=d1. Если d2=31 и d1’=30, то d2’=30, иначе d2’=d2. Правило (R7) 30E/360. Если d1 = 31, то d1’ = 30, иначе d1’=d1. Если d2=31, то d2’=30, иначе d2’=d2. Это правило является вариантом правила ISDA 30/360, используемого в основном в Европе, отсюда и буква «E» в названии правила.

Оно отличается от правила ISDA 30/360 только в том случае, если вторая дата также является 31-м числом.

Европейская версия всегда конвертирует его в 30-е число, независимо от первой даты.

Правило (R8) 30/360 PSA. Если d1 = 31 или d1 — последний день февраля, то d1’ = 30, иначе d1’=d1. Если d2=31 и d1’=30, то d2’=30, иначе d2’=d2. Скорее всего, в описании правила 30/360 SIA в [1] есть ошибка, поэтому я не привожу ее здесь.

Западная практика

Правило (W8) Основа залога 30/360. То же, что (R6) 30/360 ISDA. Другое название: 30А/360. Правило (W9) 30E/360. То же, что (R7) 30E/360. Другие названия: 30/360 ICMA, 30S/360, на основе еврооблигаций (ISDA 2006), Special German. Правило (W10) 30E/360 ISDA. Если d1 — последний день месяца, то d1’=30. Если d2 — последний день НЕ февраля, то d2’=30. Другие названия: 30E/360 ISDA, на основе еврооблигаций (ISDA 2000), немецкий.

Правило (W11) 30/360 SIA. Если d1 — последний день февраля, а d2 — последний день февраля, то d2’=30. Если d1 = 31 или последний день февраля, то d1’ = 30, иначе d1’ = d1. Если d1’=30 и d2 = 31, то d2’ = 30, иначе d2’ = d1. Правила (R4) ACT/ACT, (W1) Actual/Actual ISDA, (W2) Actual/365 Фиксированные также называются «английской практикой».

Правила (R2) ACT/360 и (W3) Actual/360 также называют «французской практикой».

Правила ISDA (R7) 30E/360, (W9) 30E/360 и (W10) 30E/360 также называются «Немецкой практикой» или «Немецкой практикой».

Итак, учитывая точные и обыкновенные проценты, а также точное и приблизительное количество дней для расчета процентов, получаем четыре метода расчета простых процентов (названия правил указаны согласно русскоязычной практике):

1. Регулярные проценты с точным количеством дней (ACT/360 – банковское правило),
2. Точные проценты с точным количеством дней (ACT/365, ACT/ACT),
3. Регулярные проценты с приблизительным количеством дней (30/360),
4. Точные проценты с приблизительным количеством дней.

А в [4] сказано: «.

вариант расчета с точными процентами и приблизительным количеством дней кредита бессмысленен и не используется».

Приведенные выше расчеты примерной продолжительности периодов в долях года показывают нетривиальность и разнообразие применяемых правил.

Их применение (как и их происхождение) зависит от страны, валюты, типа финансового инструмента, профессионального объединения, соглашений.

[1] ЗАКЛЮЧЕНИЕ: Как посчитать 3% в моем случае с ЖКХ в Украине? Анализ судебной практики по применению ст. 625 ГК Украины сказано, что обычно используется метод (Р1) ACT/365 [3], но это сформулировано не совсем четко.

Я считаю, что использовать (R4) ACT/ACT все же необходимо, и вот почему: если посчитать 3% за полный високосный год по методу ACT/365, то сумма процентов будет равна 3,008219%, что для долга (или стоимости тела кредита) в 1 млн денежных единиц даст превышение в размере 82,19 д.е.

выше 3%, которые предусмотрены годовой нормализованной процентной ставкой согласно Закону.

Это станет особенно важным при расчете прогрессивных процентов.

Буду признателен за комментарии, особенно от сотрудников банка.

Использованные источники 1) Бочаров П.

П.

, Касимов Ю.

П.

Ф.

Финансовая математика.

Москва: Гардарики, 2002. 2) Соглашение о подсчете дней, ru.wikipedia.org/wiki/Day_count_convention 3) Анализ практики применения ст. 625 ГК Украины в гражданском судопроизводстве, zib.com.ua/ua/74602-analiz_praktiki_zastosuvannya_st_625_civilnogo_kodeksu_ukrai.html 4) Четыркин Е.

М.

Финансовая математика.

Москва: Дело, 2005. 5) Правила подсчета дней и коэффициенты начисления, docs.fincad.com/support/developerfunc/mathref/Daycount.htm 6) Информационное письмо Высшего хозяйственного суда Украины № 01-06/928/2012 от 17 июля 2012 г.

, zakon.rada.gov.ua/laws/show/v_928600-12 А теперь немного кода в базе данных Oracle: Вот пакет, который я сделал специально для своего конкретного случая — он рассчитывает издержки инфляции и 3% годовых для Украины.

База данных Oracle не имеет агрегатной функции, которая умножает значения инфляции.

Вот почему я использую логарифмическое суммирование.

Скрытый текст

CREATE OR REPLACE TYPE DEBT_OVERHEAD_T as object (ID number, DEBT_DATE date, OVERHEAD_AMOUNT number); CREATE OR REPLACE TYPE DEBT_WITH_INF_AMOUNT_T as object (ID number, DEBT_DATE date, DEBT_AMOUNT number, PAYMENT_DATE date, INF_MONTH date, INF_RATE number, SKIP_INFLATION char (1), INF_RATE_ACCUMULATED number , INF_COEF_ACCUMULATED number, INF_AMOUNT_ACCUMULATED number, INF_AMOUNT_MONTH number); CREATE OR REPLACE TYPE DEBT_WITH_INF_T as object (ID number, DEBT_DATE date, DEBT_AMOUNT number, PAYMENT_DATE date, INF_MONTH date, INF_RATE number, SKIP_INFLATION char (1)); CREATE OR REPLACE TYPE DEBT_WITH_PCT_AMOUNT_T as object (ID number, DEBT_DATE date, DEBT_AMOUNT number, PAYMENT_DATE date, PCT_YEAR number, PCT_YEAR_DAYS number, PCT_YEAR_PCT_PER_DAY number, PCT_YEAR_BEGIN_DATE date , PCT_YEAR_END_DATE date, PCT_YEAR_DAYS_CALC number, PCT_YEAR_PCT_PER_YEAR number, PCT_AMOUNT_PER_YEAR number); CREATE OR REPLACE TYPE DEBT_OVERHEAD_LIST_T as table of DEBT_OVERHEAD_T; CREATE OR REPLACE TYPE DEBT_WITH_INF_AMOUNT_LIST_T as table of DEBT_WITH_INF_AMOUNT_T; CREATE OR REPLACE TYPE DEBT_WITH_INF_LIST_T as table of DEBT_WITH_INF_T; CREATE OR REPLACE TYPE DEBT_WITH_PCT_AMOUNT_LIST_T as table of DEBT_WITH_PCT_AMOUNT_T; CREATE OR REPLACE PACKAGE CALC_OVERHEADS_P is function GET_DEBT_WITH_INF (p_debt_date_begin date, p_debt_date_end date, p_last_collection_date date) return DEBT_WITH_INF_LIST_T; function GET_DEBT_WITH_INF_AMOUNT (p_debt_date_begin date, p_debt_date_end date, p_last_collection_date date) return DEBT_WITH_INF_AMOUNT_LIST_T; function GET_DEBT_WITH_INF_AMOUNT_TOTAL (p_debt_date_begin date, p_debt_date_end date, p_last_collection_date date) return DEBT_OVERHEAD_LIST_T; function GET_DEBT_WITH_PCT_AMOUNT (p_debt_date_begin date, p_debt_date_end date, p_last_collection_date date) return DEBT_WITH_PCT_AMOUNT_LIST_T; function GET_DEBT_WITH_PCT_AMOUNT_TOTAL (p_debt_date_begin date, p_debt_date_end date, p_last_collection_date date) return DEBT_OVERHEAD_LIST_T; end; / CREATE OR REPLACE PACKAGE BODY CALC_OVERHEADS_P is function GET_DEBT_WITH_INF (p_debt_date_begin date, p_debt_date_end date, p_last_collection_date date) return DEBT_WITH_INF_LIST_T is ret_value DEBT_WITH_INF_LIST_T; begin with T1 as (select a.ID, a.DEBT_DATE, a.DEBT_AMOUNT, a.PAYMENT_DATE, b.INF_MONTH, c.AVAL as INF_RATE from DEBTS a cross apply (select add_months (trunc (a.PAYMENT_DATE, 'month'), rownum - 1) as INF_MONTH from dual connect by level <= months_between (trunc (p_last_collection_date, 'month'), trunc (a.PAYMENT_DATE, 'month')) + 1) b left join INFLATION c on c.ADATE = b.INF_MONTH and c.TYP = 'M' where a.DEBT_DATE between p_debt_date_begin and p_debt_date_end ) , T2 as (select ID, DEBT_DATE, DEBT_AMOUNT, PAYMENT_DATE, INF_MONTH, INF_RATE , case when trunc (PAYMENT_DATE, 'month') = INF_MONTH and extract (day from PAYMENT_DATE) between 16 and 31 then 'Y' when trunc (p_last_collection_date, 'month') = INF_MONTH and extract (day from p_last_collection_date) between 1 and 15 then 'Y' end as SKIP_INFLATION from T1) select DEBT_WITH_INF_T (ID, DEBT_DATE, DEBT_AMOUNT, PAYMENT_DATE, INF_MONTH, INF_RATE, SKIP_INFLATION) bulk collect into ret_value from T2; return ret_value; end; function GET_DEBT_WITH_INF_AMOUNT (p_debt_date_begin date, p_debt_date_end date, p_last_collection_date date) return DEBT_WITH_INF_AMOUNT_LIST_T is ret_value DEBT_WITH_INF_AMOUNT_LIST_T; begin with T1 as (select ID, DEBT_DATE, DEBT_AMOUNT, PAYMENT_DATE, INF_MONTH, INF_RATE, SKIP_INFLATION , exp (sum (ln (case when SKIP_INFLATION = 'Y' or INF_RATE is null then 1 else INF_RATE / 100 end)) over (partition by ID order by INF_MONTH rows between unbounded preceding and current row)) * 100 as INF_RATE_ACCUMULATED from table (CALC_OVERHEADS_P.GET_DEBT_WITH_INF (p_debt_date_begin, p_debt_date_end, p_last_collection_date))) , T2 as (select ID, DEBT_DATE, DEBT_AMOUNT, PAYMENT_DATE, INF_MONTH, INF_RATE, SKIP_INFLATION, INF_RATE_ACCUMULATED , (INF_RATE_ACCUMULATED - 100) / 100 as INF_COEF_ACCUMULATED , round (((INF_RATE_ACCUMULATED - 100) / 100) * DEBT_AMOUNT, 2) as INF_AMOUNT_ACCUMULATED from T1) select DEBT_WITH_INF_AMOUNT_T (ID, DEBT_DATE, DEBT_AMOUNT, PAYMENT_DATE, INF_MONTH, INF_RATE, SKIP_INFLATION, INF_RATE_ACCUMULATED, INF_COEF_ACCUMULATED, INF_AMOUNT_ACCUMULATED , INF_AMOUNT_ACCUMULATED - lag (INF_AMOUNT_ACCUMULATED, 1, 0) over (partition by ID order by INF_MONTH)) bulk collect into ret_value from T2; return ret_value; end; function GET_DEBT_WITH_INF_AMOUNT_TOTAL (p_debt_date_begin date, p_debt_date_end date, p_last_collection_date date) return DEBT_OVERHEAD_LIST_T is ret_value DEBT_OVERHEAD_LIST_T; begin with T1 as (select ID , DEBT_DATE , round ((exp (sum (ln (case when SKIP_INFLATION = 'Y' then 1 else INF_RATE / 100 end))) - 1) * DEBT_AMOUNT, 2) as INF_AMOUNT from table (CALC_OVERHEADS_P.GET_DEBT_WITH_INF (p_debt_date_begin, p_debt_date_end, p_last_collection_date)) group by ID, DEBT_DATE, DEBT_AMOUNT) select DEBT_OVERHEAD_T (ID, DEBT_DATE, INF_AMOUNT) bulk collect into ret_va

Теги: #Алгоритмы #Финансы в ИТ #ERP-системы #oracle #База данных Oracle #финансовая математика #Расчёт инфляции #Расчёт процентов

• Что Такое Cad?

  19 Oct, 24

• Мосгорсуд Оштрафовал Google На 50 Тысяч Рублей Из-За Контекстной Рекламы В Gmail

  19 Oct, 24

• Disney Представила Собственную Систему Анимации Волос Haircontrol

  19 Oct, 24

• Подход К Глобальной Оптимизации, Основанный На Формировании Мнения В Сложных Сетях

  19 Oct, 24

• Couchbase В Сфере Телекоммуникаций

  19 Oct, 24

• Ftdi Наносит Ответный Удар

  19 Oct, 24

• Шлем Виртуальной Реальности С Сибирским Характером

  19 Oct, 24

• Подкаст «Я Сказал На Каннада» (№9)

  19 Oct, 24

• Пиратство Wi-Fi

  19 Oct, 24

• Использование Переносимых Библиотек Классов С Поддержкой Windows Phone 7.5 В Visual Studio 2013

  19 Oct, 24