В Учи.
ру мы стараемся внедрять даже небольшие улучшения с помощью A/B-тестирования; Только в этом учебном году их было более 250. A/B-тест — мощный инструмент тестирования изменений, без которого сложно представить нормальную разработку интернет-продукта.
В то же время, несмотря на кажущуюся простоту, при проведении A/B-теста можно допустить серьезные ошибки как на этапе планирования эксперимента, так и при подведении итогов.
В этой статье я расскажу о некоторых технических аспектах проведения теста: как мы определяем период тестирования, суммируем результаты и как избежать ошибочных результатов при досрочном завершении тестов и при проверке нескольких гипотез одновременно.

Типичная схема A/B-тестирования для нас (да и для многих) выглядит так:
- Мы разрабатываем фичу, но прежде чем выкатить ее на всю аудиторию, хотим убедиться, что она улучшает целевую метрику, например, вовлеченность.
- Определяем период, на который запускается тест.
- Мы случайным образом делим пользователей на две группы.
- Одной группе показываем версию продукта с функцией (экспериментальная группа), другой — старую (контрольная группа).
- В процессе мы следим за метрикой, чтобы вовремя остановить особо неудачный тест.
- После периода тестирования мы сравниваем показатели в экспериментальной и контрольной группах.
- Если метрика в экспериментальной группе статистически значимо лучше, чем в контрольной, мы распространяем тестируемую функцию на всех.
Если статистической значимости нет, завершаем тест отрицательным результатом.
Статистическая значимость, критерии и ошибки
В любом A/B-тесте есть элемент случайности: групповые метрики зависят не только от их функциональности, но и от того, какие пользователи в них включены и как они себя ведут. Чтобы достоверно сделать выводы о превосходстве группы, нужно собрать в тесте достаточное количество наблюдений, но и тогда вы не застрахованы от ошибок.Есть два типа:
- Ошибка I рода возникает, когда мы воспринимаем разницу между группами, хотя на самом деле ее нет. В тексте также появится эквивалентный термин «ложное срабатывание».
Статья посвящена именно таким ошибкам.
- Ошибка второго типа возникает, если мы фиксируем отсутствие разницы, хотя на самом деле она есть.
Его можно контролировать с помощью статистических методов.
Например, мы хотим, чтобы в каждом эксперименте вероятность ошибки I рода не превышала 5% (это просто удобное значение, для своих нужд можно взять другое).
Тогда примем эксперименты на уровне значимости 0,05:
- Существует A/B-тест с контрольной группой A и экспериментальной группой B. Цель — проверить, отличается ли группа B от группы A по некоторым показателям.
- Сформулируем нулевую статистическую гипотезу: группы А и Б не различаются, а наблюдаемые различия объясняются шумом.
По умолчанию мы всегда предполагаем, что разницы нет, пока не доказано обратное.
- Проверяем гипотезу строгим математическим правилом – статистическим критерием, например, тестом Стьюдента.
- В результате мы получаем p-значение.
Оно варьируется от 0 до 1 и представляет собой вероятность увидеть текущую или более экстремальную разницу между группами, если нулевая гипотеза верна, то есть если между группами нет разницы.
- Значение p сравнивается с уровнем значимости 0,05. Если оно больше, мы принимаем нулевую гипотезу об отсутствии различий, в противном случае мы предполагаем, что между группами существует статистически значимая разница.
Параметрические основаны на параметрах выборочного распределения случайной величины и имеют большую мощность (меньше допускают ошибок второго рода), но накладывают требования к распределению исследуемой случайной величины.
Наиболее распространенным параметрическим тестом является t-критерий Стьюдента.
Для двух независимых выборок (в случае A/B-теста) его иногда называют тестом Уэлча.
Этот критерий работает корректно, если исследуемые значения имеют нормальное распределение.
Может показаться, что это требование почти никогда не выполняется в реальных данных, но на самом деле тест требует нормального распределения средних выборок, а не самих выборок.
На практике это означает, что критерий можно использовать, если у вас в тесте довольно много наблюдений (десятки или сотни) и в распределениях нет очень длинных хвостов.
В этом случае характер распределения исходных наблюдений неважен.
Читатель может самостоятельно убедиться, что t-критерий Стьюдента работает правильно даже на выборках, полученных на основе распределения Бернулли или экспоненциального распределения.
Среди непараметрических тестов популярен критерий Манна-Уитни.
Его стоит использовать, если ваши выборки очень малы или есть большие выбросы (метод сравнивает медианы, поэтому он устойчив к выбросам).
Также для корректной работы критерия в выборках должно быть мало совпадающих значений.
На практике нам никогда не приходилось использовать непараметрические тесты; в наших тестах мы всегда используем тест Стьюдента.
Проблема проверки множественных гипотез
Самая очевидная и простая проблема: если в тесте помимо контрольной группы есть несколько экспериментальных, то суммирование результатов с уровнем значимости 0,05 приведет к многократному увеличению доли ошибок I рода.Это происходит потому, что каждый раз, когда применяется статистический тест, вероятность ошибки I рода будет составлять 5%.
По количеству групп
и уровень значимости
Вероятность того, что какая-либо экспериментальная группа случайно выиграет, равна:
Например, по трем экспериментальным группам мы получаем 14,3% вместо ожидаемых 5%.
Проблема решается применением поправки Бонферрони для множественной проверки гипотез: нужно просто разделить уровень значимости на количество сравнений (то есть групп) и работать с ним.
Для приведенного выше примера уровень значимости с учетом поправки составит 0,05/3 = 0,0167, а вероятность хотя бы одной ошибки I рода составит приемлемые 4,9%.
Метод Хольма-Бонферрони Искушенный читатель знает также о методе Холма-Бонферрони, который всегда имеет большую мощность, чем поправка Бонферрони, то есть реже допускает ошибки второго типа.
В этом методе мы сортируем
гипотез путем увеличения значений p и начинаем сравнивать их по порядку с необходимым уровнем значимости, который увеличивается в зависимости от номера шага
в соответствии с формулой:
P-значение первой гипотезы сравнивается с уровнем статистической значимости.
.
Если гипотеза принята, то переходим ко второй и сравниваем ее p-значение с уровнем статистической значимости.
, и так далее.
Как только гипотеза отвергается, процесс останавливается, и все оставшиеся гипотезы также отвергаются.
Наиболее жесткие требования (и такие же, как и в поправке Бонферрони) предъявляются к гипотезе с наименьшим значением p, а большая мощность достигается за счет менее жестких условий для последующих гипотез.
Цель A/B-теста — выбрать одного победителя, поэтому методы Бонферрони и Холма-Бонферрони в этом приложении абсолютно идентичны.
Строго говоря, сравнения между группами на основе разных показателей или сегментов аудитории также подвержены проблеме множественного тестирования.
Формально учесть все проверки довольно сложно, поскольку их количество сложно предсказать заранее и иногда они не являются независимыми (особенно если речь идет о разных метриках, а не срезах).
Универсального рецепта не существует, полагайтесь на здравый смысл и помните, что если проверять много разделов по разным метрикам, то в любом тесте можно увидеть якобы статистически значимый результат. Это означает, что нам следует опасаться, например, значительного увеличения удержания на пятый день новых мобильных пользователей из крупных городов.
Проблема вуайеризма
Особым случаем проверки множественных гипотез является проблема подглядывания.Идея состоит в том, что значение p может случайно упасть ниже принятого уровня значимости по ходу теста.
Если внимательно следить за экспериментом, то можно уловить такой момент и ошибочно сделать вывод о статистической значимости.
Предположим, мы отклонились от схемы тестирования, описанной в начале поста, и решили суммировать результаты на уровне значимости 5% каждый день (или просто не один раз за время теста).
Под обобщением я имею в виду объявление теста положительным, если значение p ниже 0,05, и продолжение в противном случае.
При такой стратегии доля ложноположительных результатов будет пропорциональна количеству проверок и достигнет 28% в первый месяц.
Такая огромная разница кажется нелогичной, поэтому давайте обратимся к методике A/A-тестирования, которая незаменима при разработке схем A/B-тестирования.
Идея A/A-теста проста: смоделировать множество A/B-тестов на исторических данных со случайным разделением на группы.
Очевидно, что разницы между группами нет, поэтому вы можете точно оценить долю ошибок I рода в вашей схеме A/B-тестирования.
На гифке ниже показано, как меняются значения p по дням для четырех таких тестов.
Уровень значимости 0,05 обозначен пунктирной линией.
Когда значение p опускается ниже, мы окрашиваем тестовый график в красный цвет. Если бы в это время были подведены итоги испытания, его можно было бы считать успешным.

Аналогично посчитаем 10 тысяч А/А-тестов длительностью один месяц и сравним долю ложноположительных результатов в схеме с суммированием результатов в конце периода и каждый день.
Для ясности мы представляем графики отклонения значения p по дням для первых 100 симуляций.
Каждая линия — это p-значение одного теста, красным выделены траектории тестов, которые в конечном итоге были ошибочно признаны успешными (чем меньше, тем лучше), пунктир — необходимое p-значение для признания теста успешным.
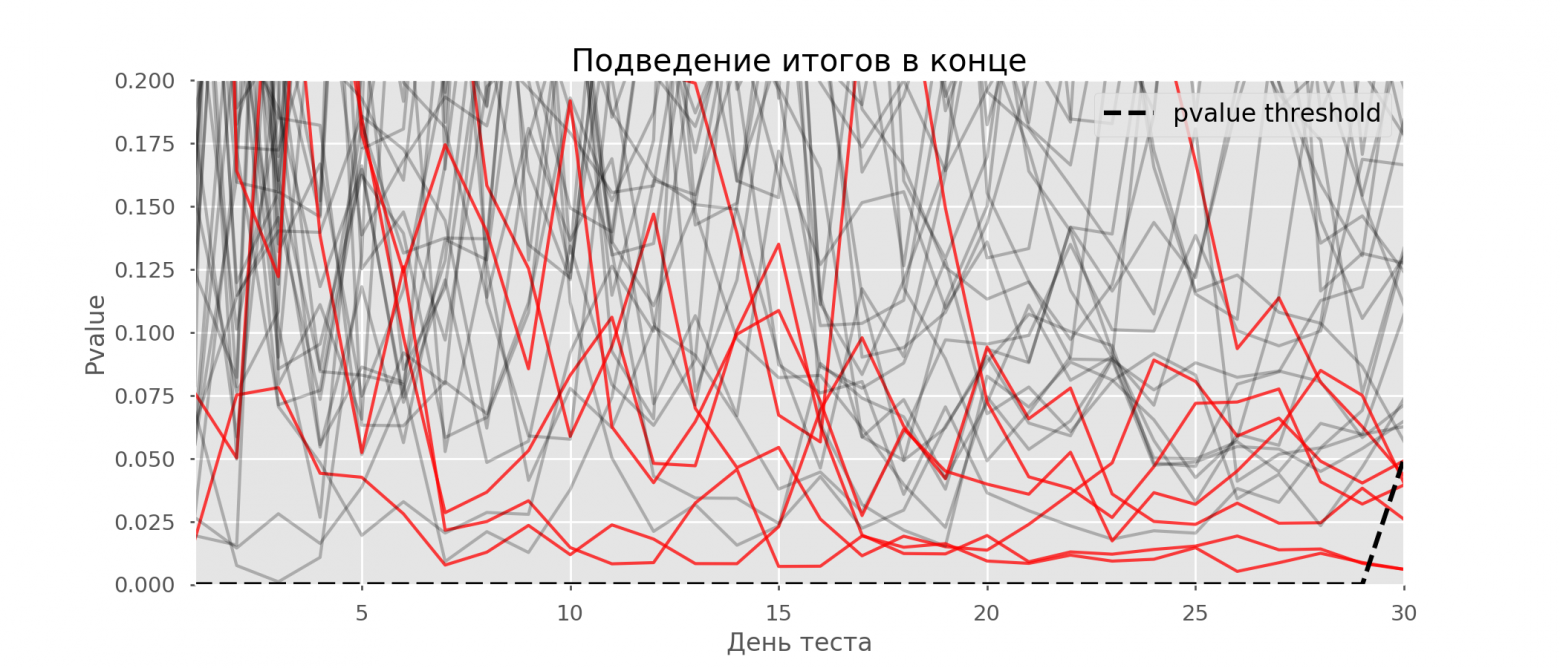
На графике можно насчитать 7 ложноположительных тестов, а всего среди 10 тысяч их оказалось 502, или 5%.
Хотелось бы отметить, что р-значения многих тестов во время наблюдений падали ниже 0,05, но к концу наблюдений вышли за пределы уровня значимости.
Теперь оценим схему тестирования с подведением результатов каждый день: 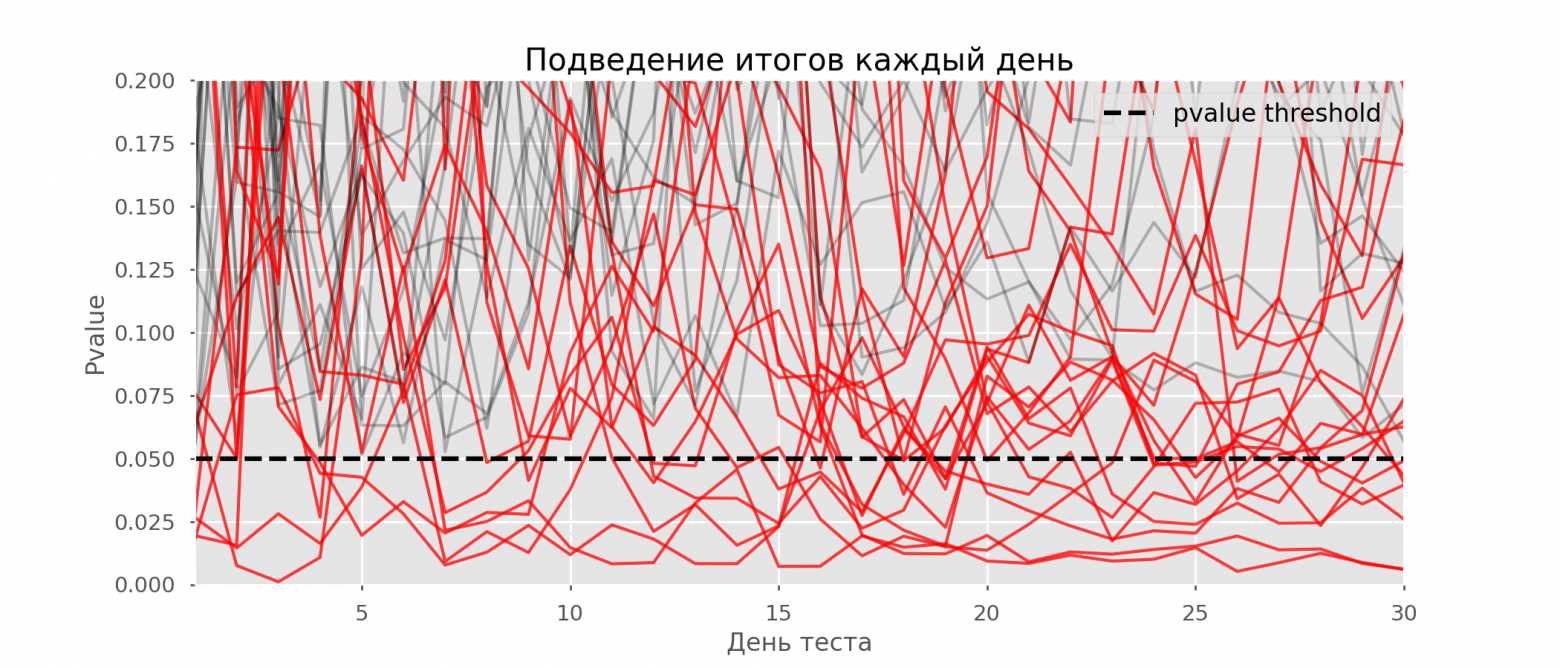
Красных линий так много, что уже ничего не понятно.
Перерисуем, обрезав тестовые линии, как только их значение p достигнет критического значения: 
Всего ложноположительных тестов будет 2813 из 10 тысяч, или 28%.
Понятно, что такая схема нежизнеспособна.
Хотя проблема слежения является частным случаем множественного тестирования, применять здесь стандартные поправки (Бонферрони и др.
) не стоит, поскольку они окажутся излишне консервативными.
На графике ниже показана доля ложноположительных результатов в зависимости от количества протестированных групп (красная линия) и количества просмотров (зеленая линия).
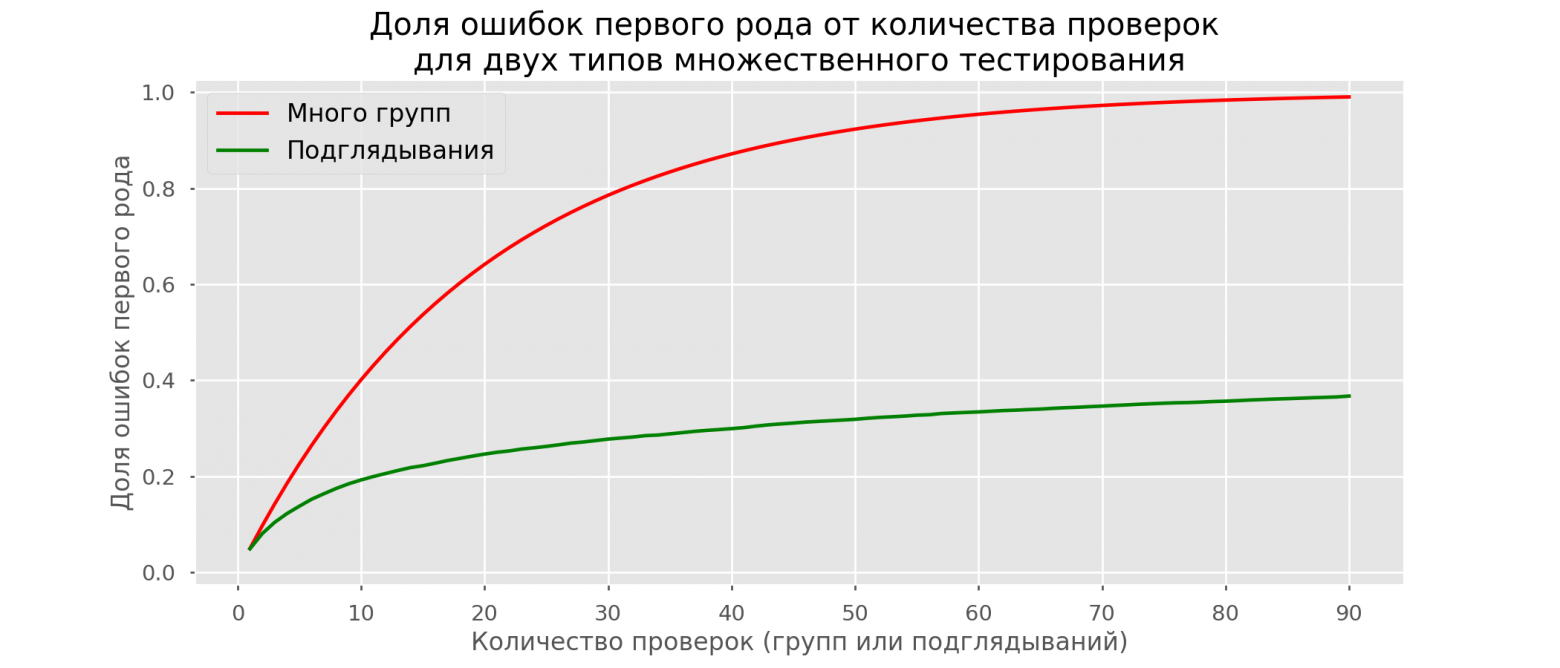
Хотя на бесконечности и в вуайеризме мы очень близко подойдем к 1, доля ошибок растет гораздо медленнее.
Это объясняется тем, что сравнения в этом случае уже не являются независимыми.
Байесовский подход и проблема вуайеризма Можно встретить мнение, что байесовский подход к анализу A/B-тестов устраняет проблему слежки.
Это не так, хотя это можно настроить соответствующим образом.
Прекрасную статью с дополнительными материалами можно прочитать Здесь .
Способы досрочного завершения теста
Существуют варианты тестирования, которые позволяют вам пройти тест раньше.Расскажу о двух из них: с постоянным уровнем значимости (поправка Покока) и зависящем от числа подглядывающих (поправка О’Брайена-Флеминга).
Строго говоря, для обеих поправок нужно заранее знать максимальную продолжительность теста и количество проверок между началом и окончанием теста.
При этом проверки должны происходить примерно через равные промежутки времени (или после равного количества наблюдений).
Покок
Метод заключается в том, что мы каждый день суммируем результаты тестов, но на пониженном (более строгом) уровне значимости.Например, если мы знаем, что будем делать не более 30 проверок, то уровень значимости следует установить 0,006 (выбирается в зависимости от количества просмотров методом Монте-Карло, то есть эмпирически).
В нашей симуляции мы получаем 4% ложных срабатываний — видимо, порог можно было бы увеличить.
Несмотря на кажущуюся наивность, некоторые крупные компании используют этот метод. Это очень просто и надежно, если вы принимаете решения на основе чувствительных метрик и высокого трафика.
Например в Авито по умолчанию уровень значимости принят равным 0,005 .
О'Брайен-Флеминг
В этом методе уровень значимости варьируется в зависимости от номера теста.Необходимо заранее определить количество шагов (или пиков) в тесте и рассчитать уровень значимости для каждого из них.
Чем раньше мы попытаемся завершить тест, тем более строгий критерий будет применен.
Пороги t-статистики Стьюдента
(включая значение на последнем шаге
), соответствующие желаемому уровню значимости, зависят от номера теста
(принимает значения от 1 до общего количества проверок
включительно) и рассчитываются по формуле, полученной опытным путем:
Код для воспроизведения шансов
Соответствующие уровни значимости рассчитываются через процентильfrom sklearn.linear_model import LinearRegression from sklearn.metrics import explained_variance_score import matplotlib.pyplot as plt # datapoints from https://www.aarondefazio.com/tangentially/Эp=83 total_steps = [ 2, 3, 4, 5, 6, 8, 10, 15, 20, 25, 30, 50, 60 ] last_z = [ 1.969, 1.993, 2.014, 2.031, 2.045, 2.066, 2.081, 2.107, 2.123, 2.134, 2.143, 2.164, 2.17 ] features = [ [1/t, 1/t**0.5] for t in total_steps ] lr = LinearRegression() lr.fit(features, last_z) print(lr.coef_) # [ 0.33729346, -0.63307934] print(lr.intercept_) # 2.247105015502784 print(explained_variance_score(lr.predict(features), last_z)) # 0.999894 total_steps_extended = np.arange(2, 80) features_extended = [ [1/t, 1/t**0.5] for t in total_steps_extended ] plt.plot(total_steps_extended, lr.predict(features_extended)) plt.scatter(total_steps, last_z, s=30, color='black') plt.show()
стандартное распределение, соответствующее значению t-статистики Стьюдента
:
perc = scipy.stats.norm.cdf(Z)
pval_thresholds = (1 − perc) * 2
В тех же симуляциях это выглядит так:

Ложноположительный результат составил 501 из 10 тысяч, или ожидаемые 5%.
Обратите внимание, что уровень значимости не достигает 5% даже в конце, так как эти 5% надо «размазать» по всем тестам.
В компании мы используем именно эту поправку, если запускаем тест с возможностью досрочной остановки.
Об этих и других поправках вы можете прочитать на сайте связь .
Оптимизационный метод Оптимизационный метод хорош тем, что позволяет вообще не фиксировать дату окончания теста, а необходимый уровень значимости рассчитывается в каждый момент времени как функция количества наблюдений в тесте.
Интуитивно лично мне их метод нравится меньше, так как в нем строгость критерия возрастает по мере прохождения теста.
То есть он минимален в первые дни, когда случайный шум оказывает наибольшее влияние на метрики.
В методе О'Брайена-Флеминга ситуация противоположная.
Калькулятор A/B-тестирования
Специфика нашего продукта такова, что распределение любой метрики сильно варьируется в зависимости от аудитории теста (например, номера класса) и времени года.Поэтому в качестве даты окончания теста нельзя будет принять правила типа «тест завершится, когда в каждой группе будет 1 миллион пользователей» или «тест завершится, когда количество решенных задач достигнет 100 миллионов».
То есть получится, но на практике придется учитывать слишком много факторов:
- какие классы включены в тест;
- тест раздается преподавателям или учащимся;
- время учебного года;
- тестируйте для всех пользователей или только для новых.
Для прогнозирования продолжительности тестирования мы разработали внутреннее приложение — калькулятор A/B-тестов.
На основе активности пользователей из выбранного сегмента за последний год приложение рассчитывает период, за который необходимо запустить тест, чтобы существенно зафиксировать подъем на Х% по выбранной метрике.
Также автоматически учитывается поправка на многократное тестирование и рассчитываются пороговые уровни значимости для досрочной остановки теста.

Все наши метрики рассчитываются на уровне тестовых объектов.
Если метрикой является количество решенных задач, то в тесте на уровне преподавателя это будет сумма задач, решенных его учениками.
Поскольку мы используем t-критерий Стьюдента, мы можем заранее рассчитать необходимые калькулятору агрегаты для всех возможных разделов.
За каждый день с начала теста необходимо знать количество человек в тесте
, среднее значение показателя
и его дисперсия
.
Зафиксировав доли контрольной группы
, экспериментальная группа
и ожидаемая выгода от теста
в процентах можно рассчитать ожидаемые значения t-статистики Стьюдента
и соответствующее значение p для каждого тестового дня:
Далее легко получить значения p для каждого дня: pvalue = (1 − scipy.stats.norm.cdf(ttest_stat_value)) * 2
Зная значение p и уровень значимости с учетом всех поправок для каждого дня теста, для любой продолжительности теста, можно рассчитать минимальное повышение, которое можно обнаружить (в англоязычной литературе — MDE, минимальный обнаруживаемый эффект).
После этого легко решить обратную задачу – определить количество дней, необходимое для выявления ожидаемого подъема.
Заключение
В заключение хотелось бы напомнить основные посылы статьи:- Если вы сравниваете средние значения показателя по группам, скорее всего, подойдет t-критерий Стьюдента.
Исключением являются крайне малые размеры выборки (десятки наблюдений) или аномальные распределения метрики (на практике я с подобным не сталкивался).
- Если в тесте несколько групп, используйте поправки для проверки нескольких гипотез.
Подойдет простейшая поправка Бонферрони.
- Сравнения, основанные на дополнительных показателях или срезах групп, также подвержены проблеме многократного тестирования.
- Заранее выберите дату завершения теста.
Вместо даты вы также можете записать количество наблюдений в группе.
- Не отправляйте результаты анализов раньше этой даты.
Это можно сделать только в том случае, если вы заранее решили использовать методы, допускающие досрочное прекращение, например метод О'Брайена-Флеминга.
- Всякий раз, когда вы вносите изменения в схему A/B-тестирования, всегда проверяйте ее жизнеспособность с помощью A/A-тестов.
Иногда можно выкатить функционал всем, кто не показал существенного прироста в тесте; некоторые изменения неизбежно происходят вообще без тестирования.
Но если вы проводите сотни тестов в год, точный анализ особенно важен.
В противном случае есть риск, что количество ложноположительных тестов будет сопоставимо с действительно полезными.
Теги: #математика #аналитика #Веб-аналитика #Визуализация данных #анализ данных #Интеллектуальный анализ данных #статистика #A/B-тестирование

-
Школьная Задача По Физике
19 Oct, 24 -
Новые Города В Myclime
19 Oct, 24 -
Пересчет Хабрасилы И Рейтинга
19 Oct, 24


