В этой статье я расскажу о достаточно важной теме в информатике и теории автоматов — минимизации булевых функций.
Этим вопросом задавался пожалуй каждый, кто изучал или сталкивался с этой темой.
Существует множество методов, но наибольший интерес представляют те, которые можно без особого труда формализовать и соответствующим образом запрограммировать.
А также работа с произвольными логическими выражениями.
Идеального метода не существует; у каждого есть определенные слабые и сильные качества.
Я остановлюсь на так называемом методе Гиперкуба – метод Куайна .
Метод, к сожалению, применим только для Совершенных ДНФ, поэтому при большом количестве переменных использование усложняется гигантским выражением SDNF. Способ заключается в применении известных правил адгезии и впитывания.
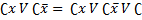

Прежде чем описывать алгоритм, объясню, почему метод называется методом гиперкуба.
Возьмем произвольную функцию f, M1(f) — единичное множество.
Проще говоря, набор наборов переменных, на которых функция превращается в истинное утверждение.
Гиперкуб – это множество M1(f).
Конъюнктивный моном импликантен, если M1(K) включен в M1(f).
Импликанта называется простой, если не существует другого К2 такого, что М1(К) содержится в М1(К2), проще говоря — соответствует наибольшему гиперкубу.
Основные этапы этого метода
- Построить таблицу истинности.
- Выпишите все гиперкубы из M1(f) и импликанты.
- Возьмем простые импликанты.
- Постройте покрывающий стол.
- Создайте тупиковую DNF из оставшихся основных импликантов.
В качестве примера возьмем следующую логическую функцию.
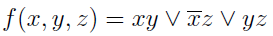
Построим для него таблицу истинности: 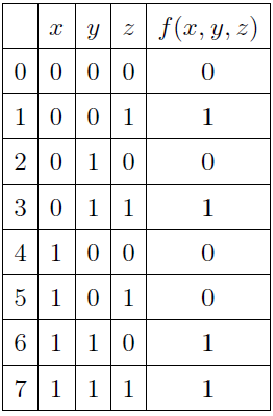
Выпишем все гиперкубы, лежащие в M1(f) и соответствующие им импликанты: 
Выбираем простые импликанты и строим таблицу их покрытия: 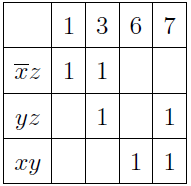
Поскольку импликант yz перекрывается с другими, его можно удалить из выражения.
Получается, что тупиковая ДНФ-функция имеет вид: 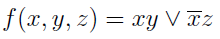
Рекомендую всем, кому интересно прочитать замечательную книгу К.
Г.
Самофалов «Прикладная теория цифровых автоматов».
Теги: #теория автоматов #теория автоматов #метод Куайна #минимизация логических функций #гиперкуб #Алгоритмы
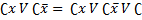
-
Стек Dots: C++ И C#
19 Oct, 24 -
Пасхальный Расчет
19 Oct, 24 -
Великая Выкачка, Или Вперёд В Кайнозой
19 Oct, 24 -
Java В Android: Грядут Перемены (Слухи)
19 Oct, 24 -
Новые Типы Файлов В Google Docs
19 Oct, 24 -
Время Забросить Свои Сети
19 Oct, 24 -
Обновление Интерфейса Gmail
19 Oct, 24


